 推荐阅读
推荐阅读
【01】直角三角形中45°处理的40种方法
【02】一题可破万题山之一道好题的多解多变归一
【03】培优拔高 | 初中最值问题的19大类型
【04】神仙试题 | 一道二次函数,经典二十问!
【05】多解 | 勾股定理的16种典型证明方法
【06】最值之将军饮马、将军遛马、将军过河
【07】名师之作:几何最值问题大一统
【08】经典几何模型之“阿式圆”
【09】以一道真题谈变式教学的归一思想
【10】一题多变/一题多问/一题多解/一 一聚多
【11】重难点突破 | 圆题型汇编(精)(附Word)
【12】模型解题 | 巧构辅圆解难题(一题多解)
【13】动态展示 | 圆与切线所涉及的25个经典模型
温馨提示: 点击图片,可查看大图 01.平行于弦的半径 课本上有垂直于弦的半(直)径,即垂径定理,知二推三, 平行于弦的半径也是有特殊之处的。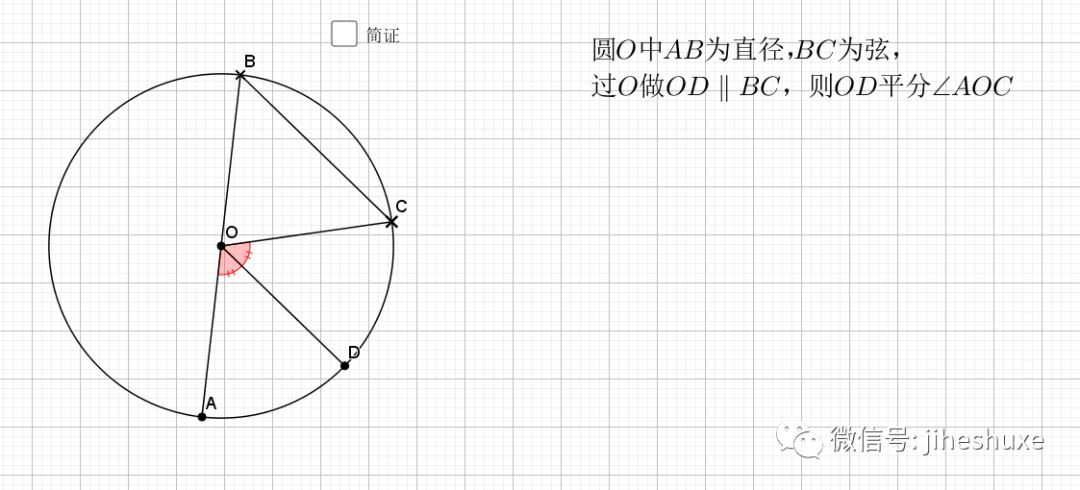
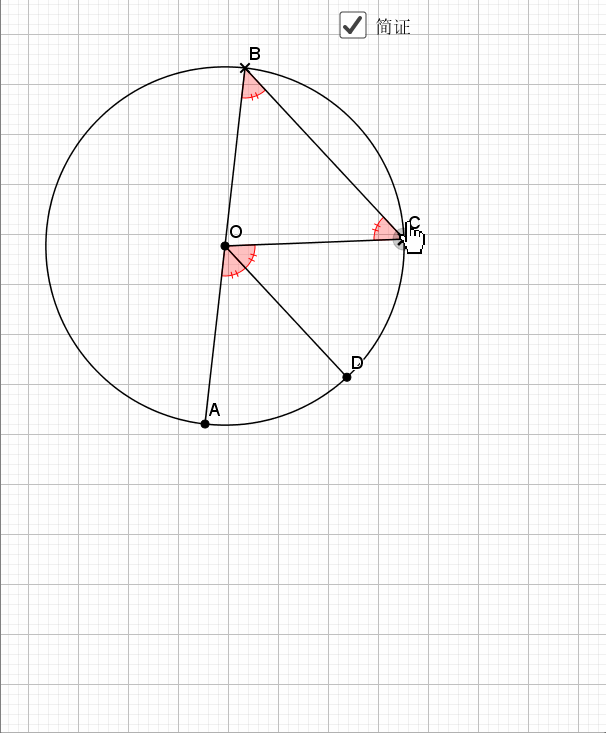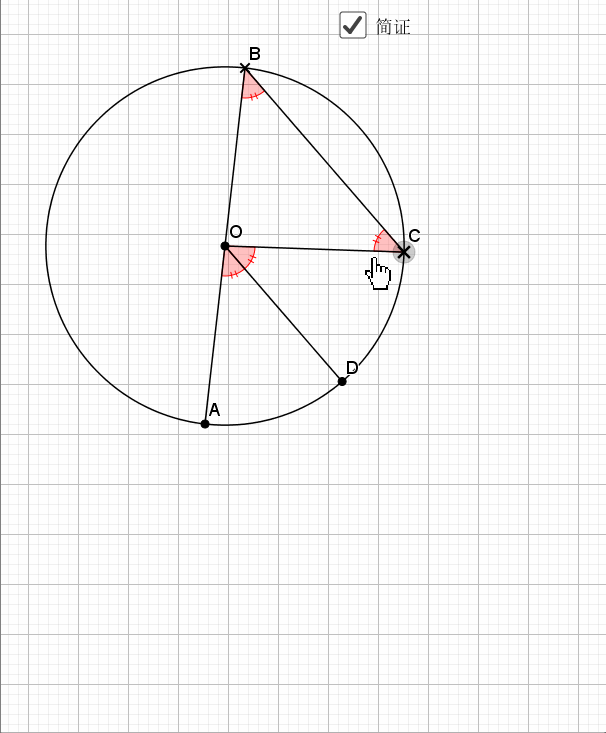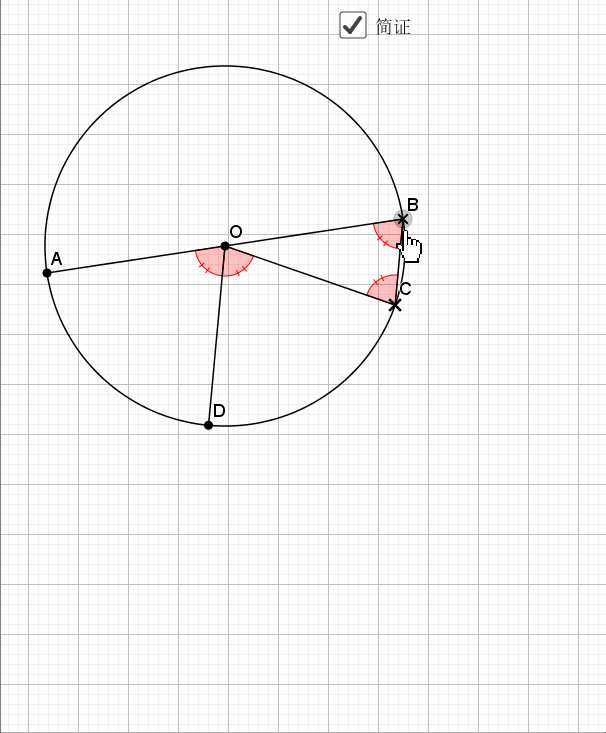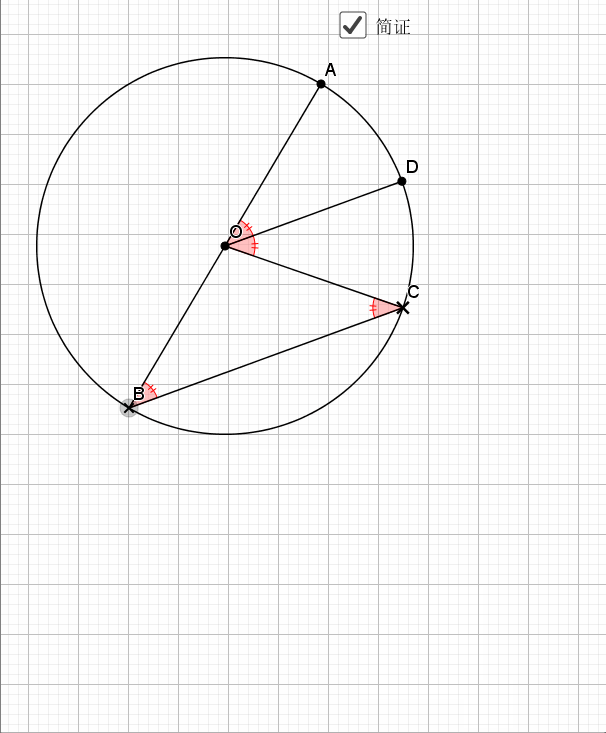
又用到了经典的知二推一 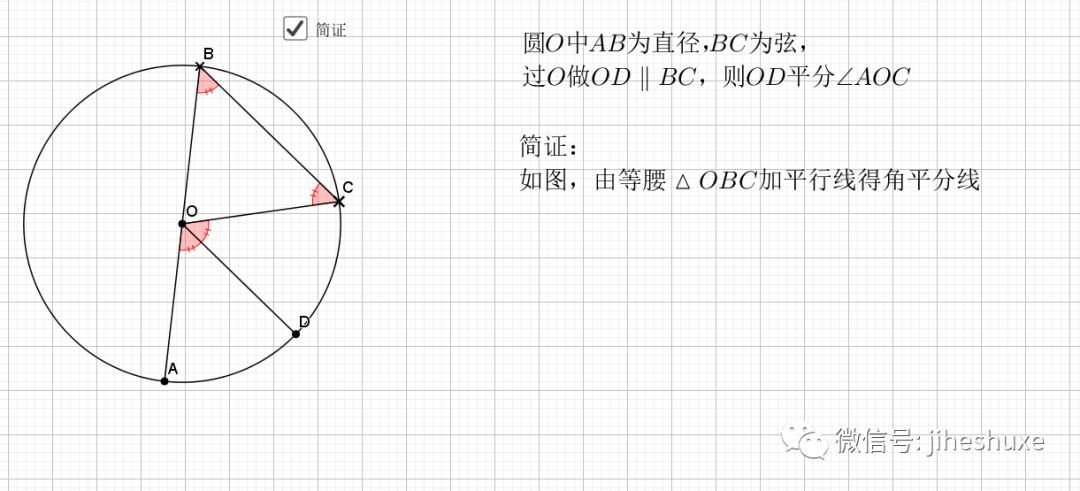
02.内外平分线
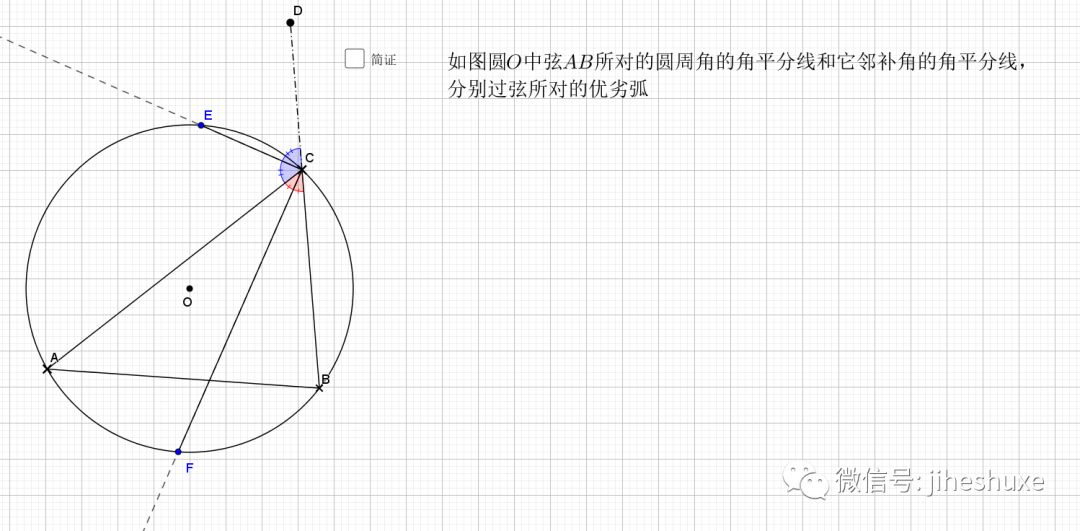
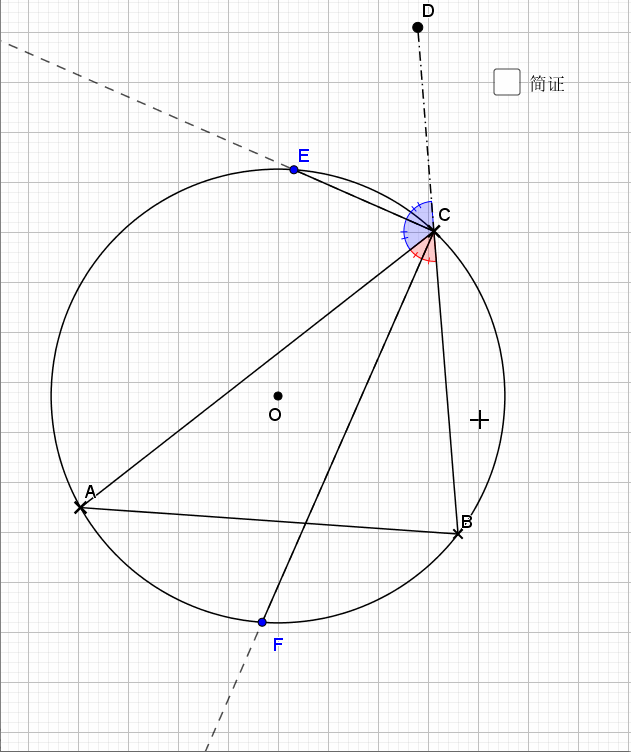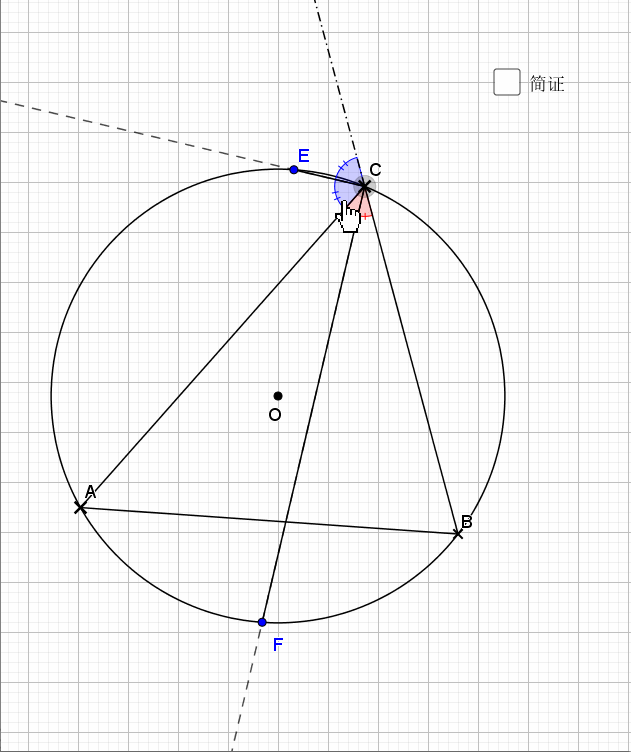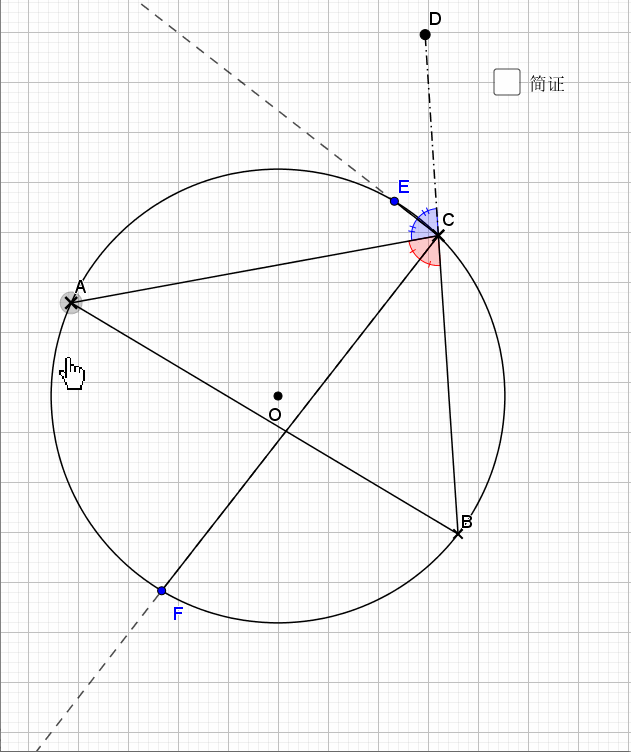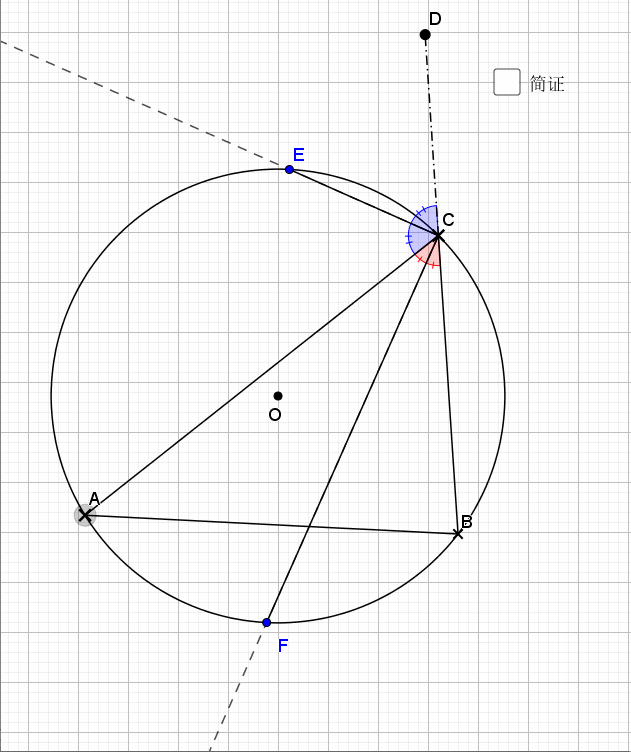
由刚才结论,加上垂径定理结论即可
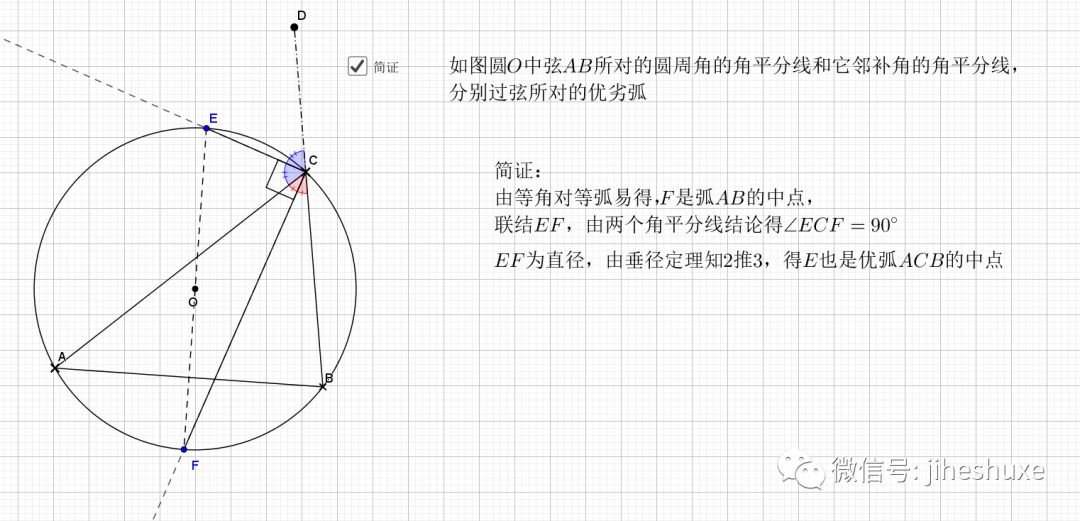
03.特别圆周角的平分线
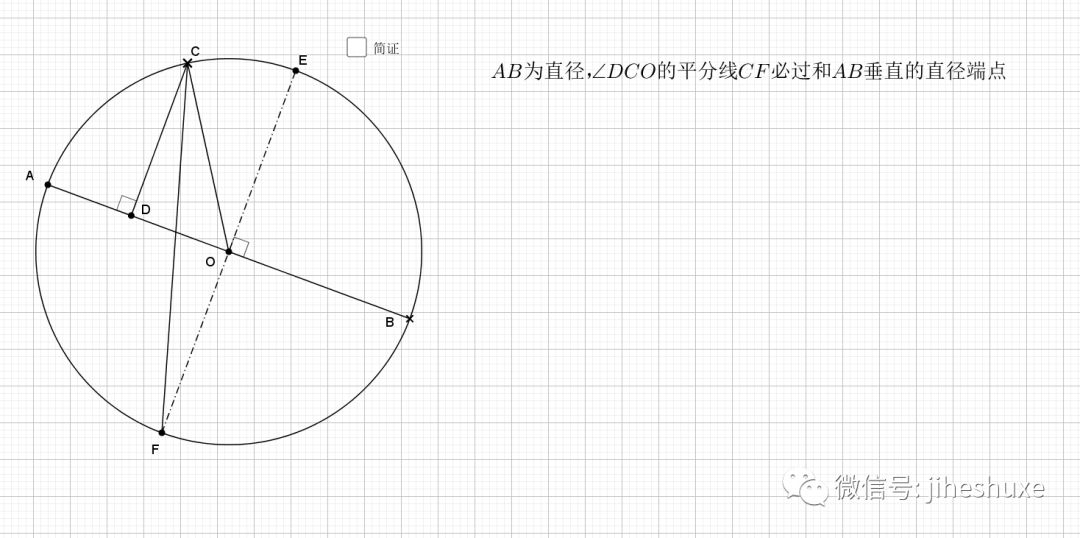
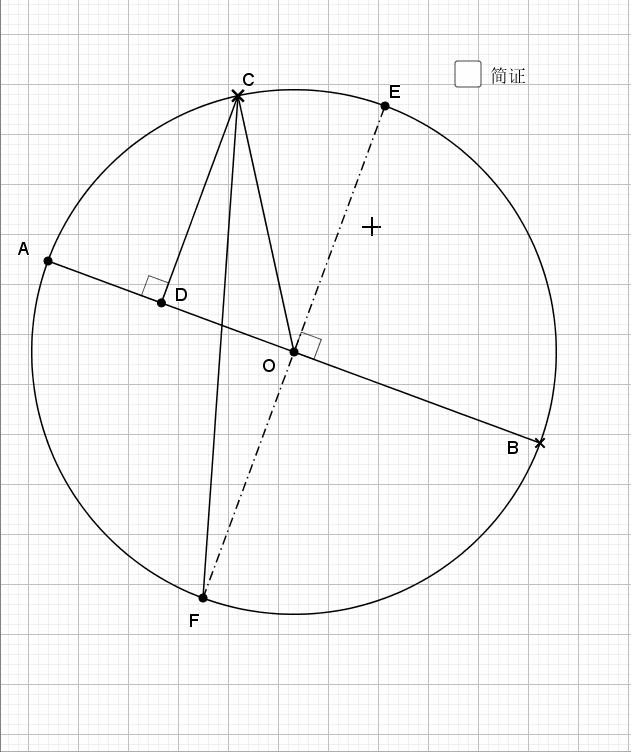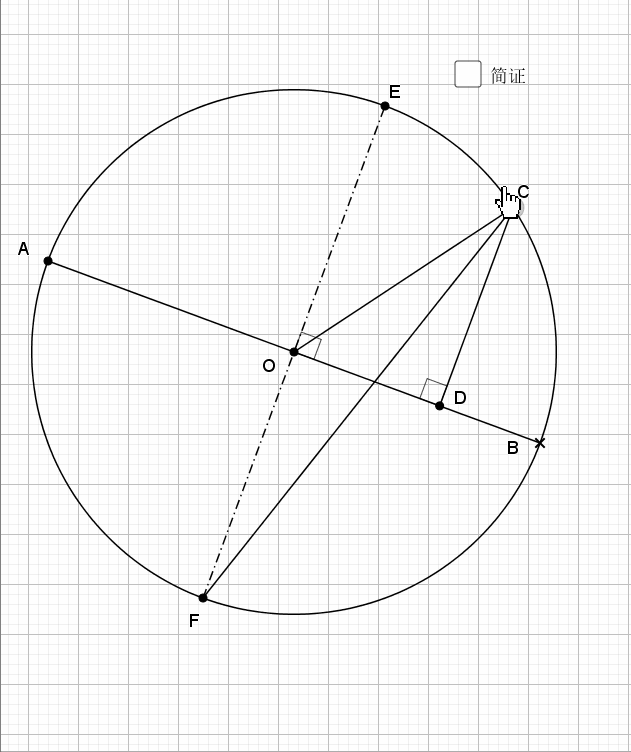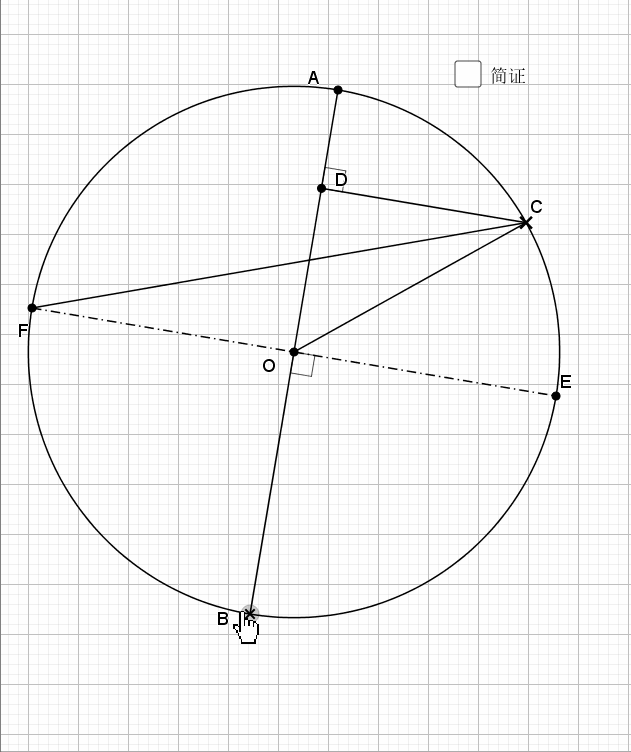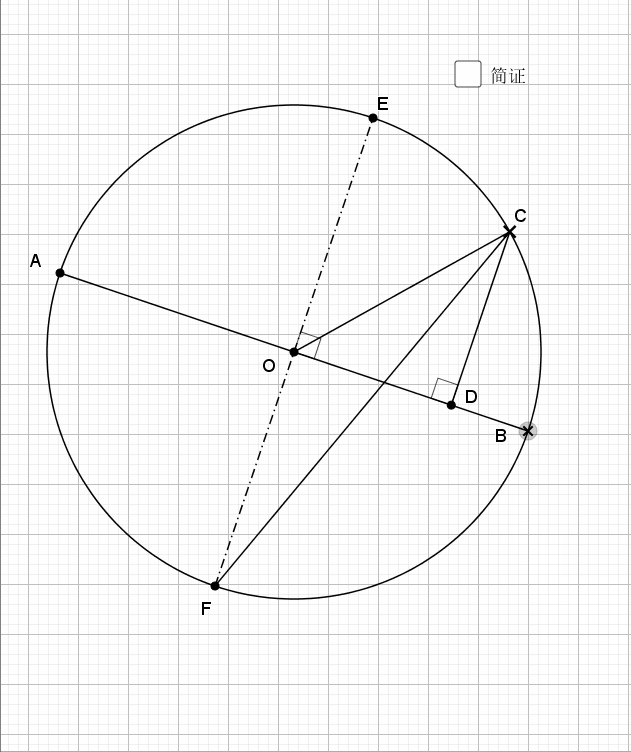
依然利用知二推一即可得
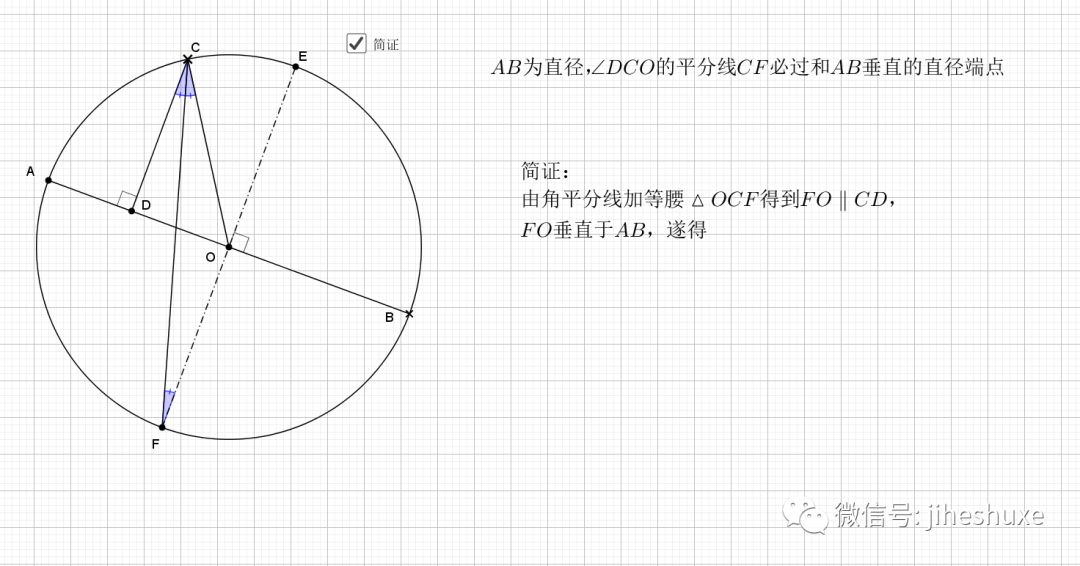
04.相交圆三倍弧
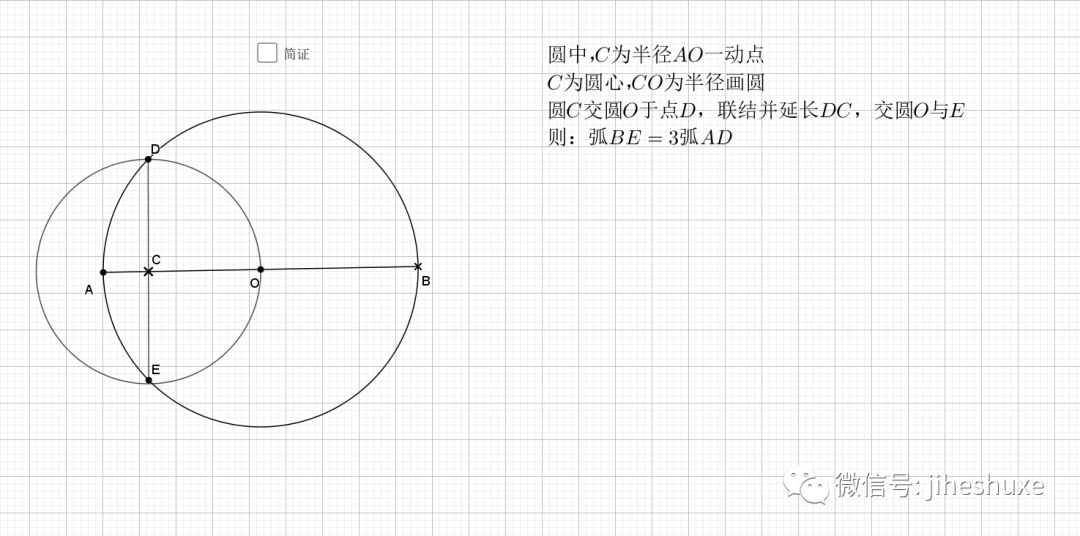
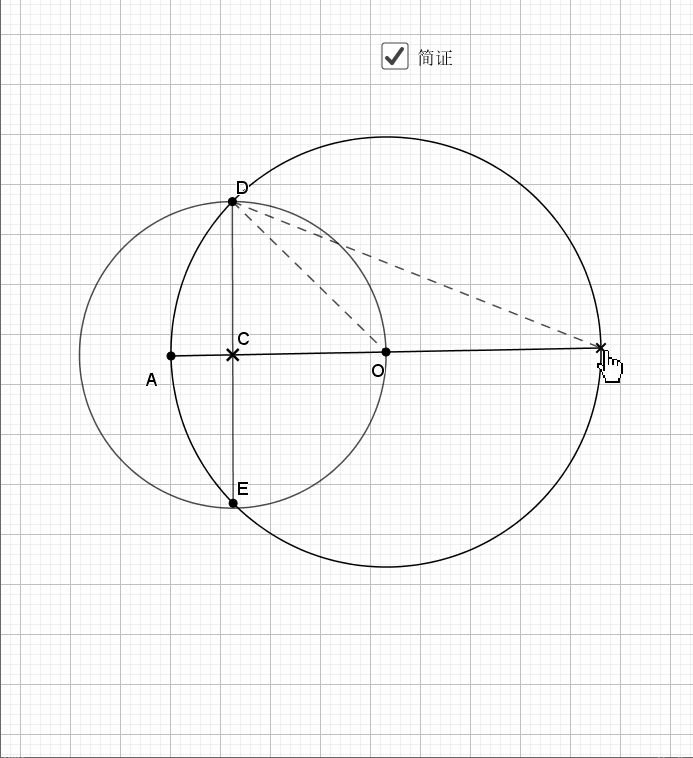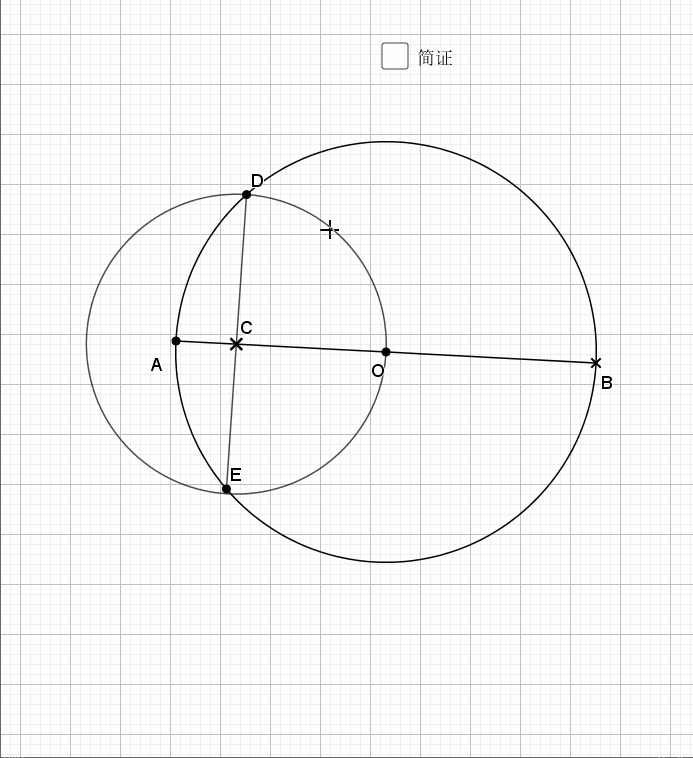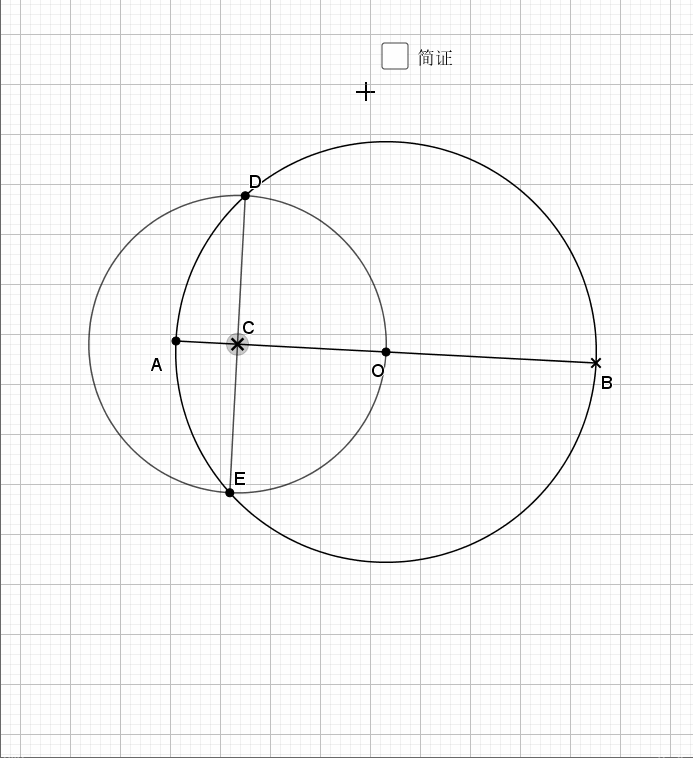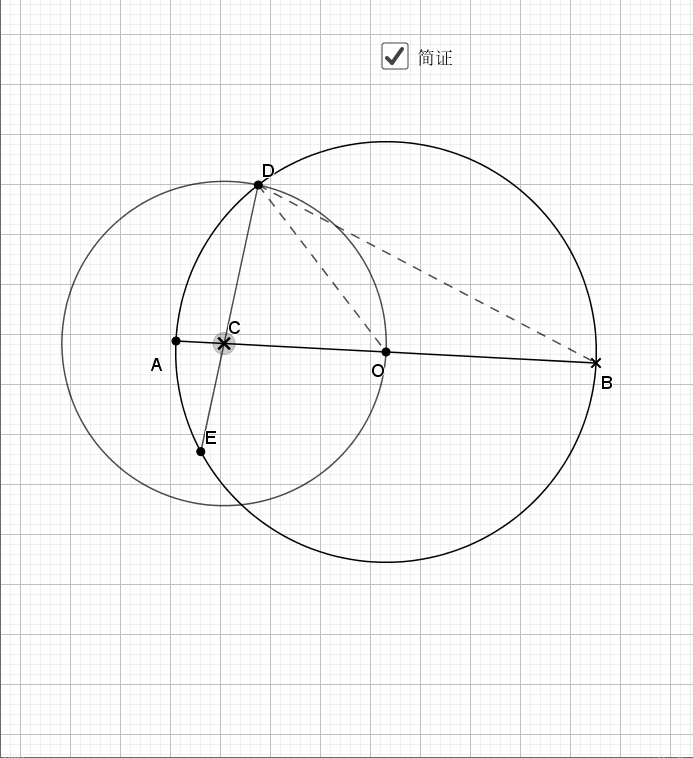
利用圆周角的倍数关系就是弧的倍数关系
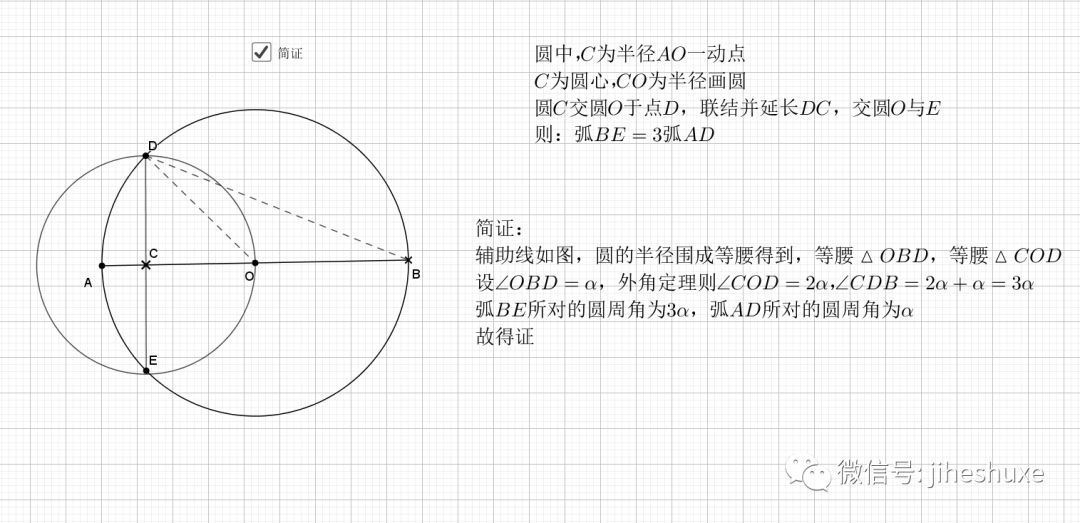
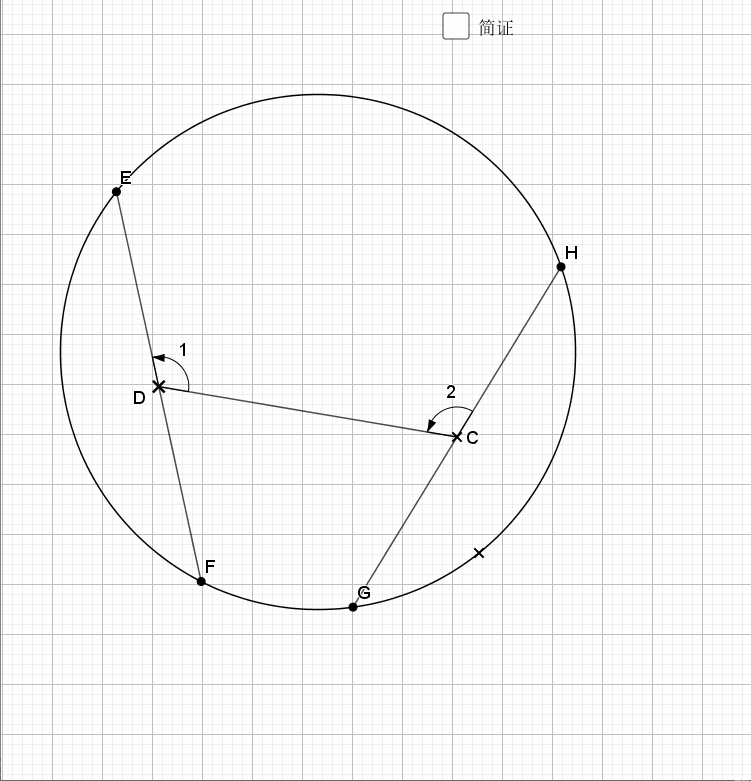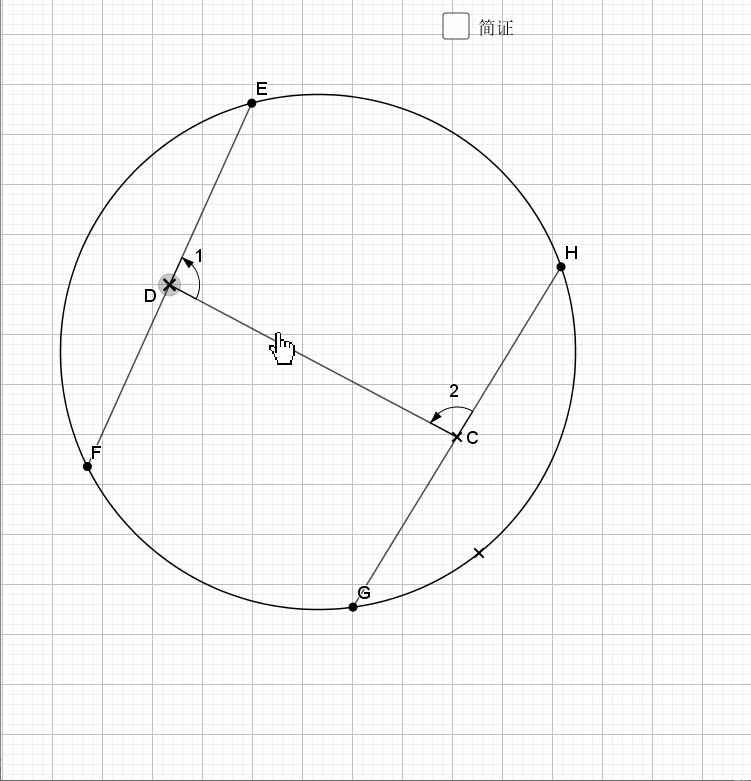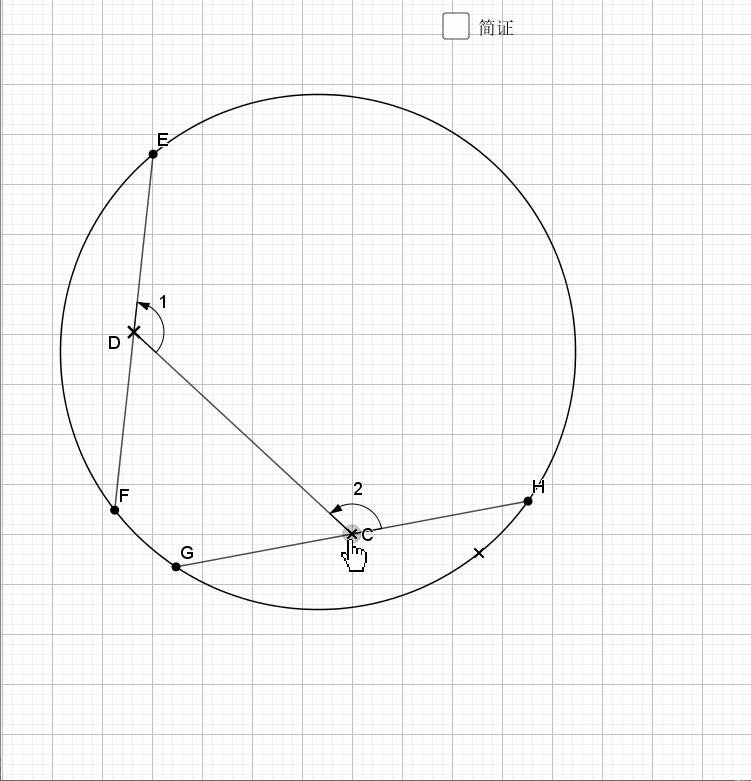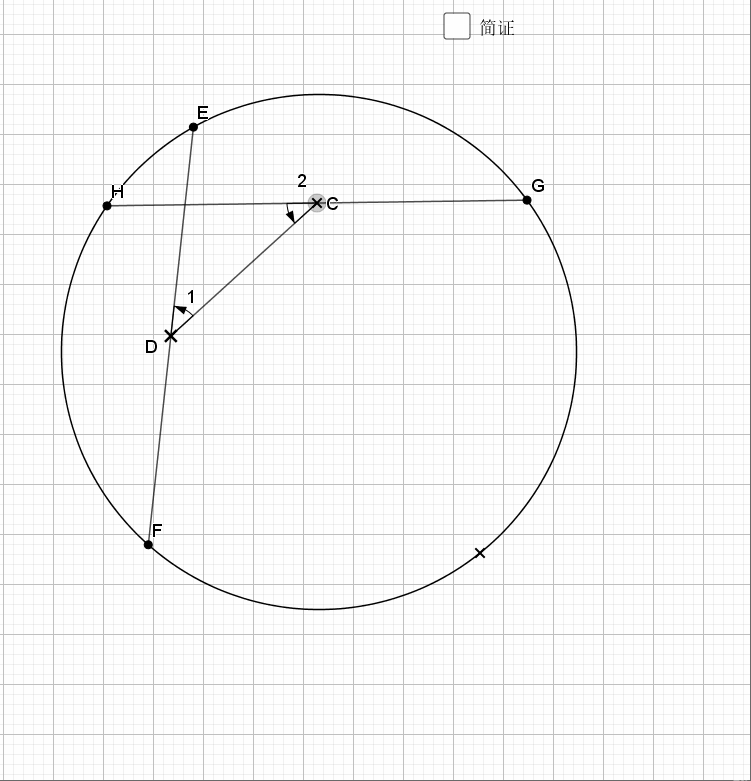
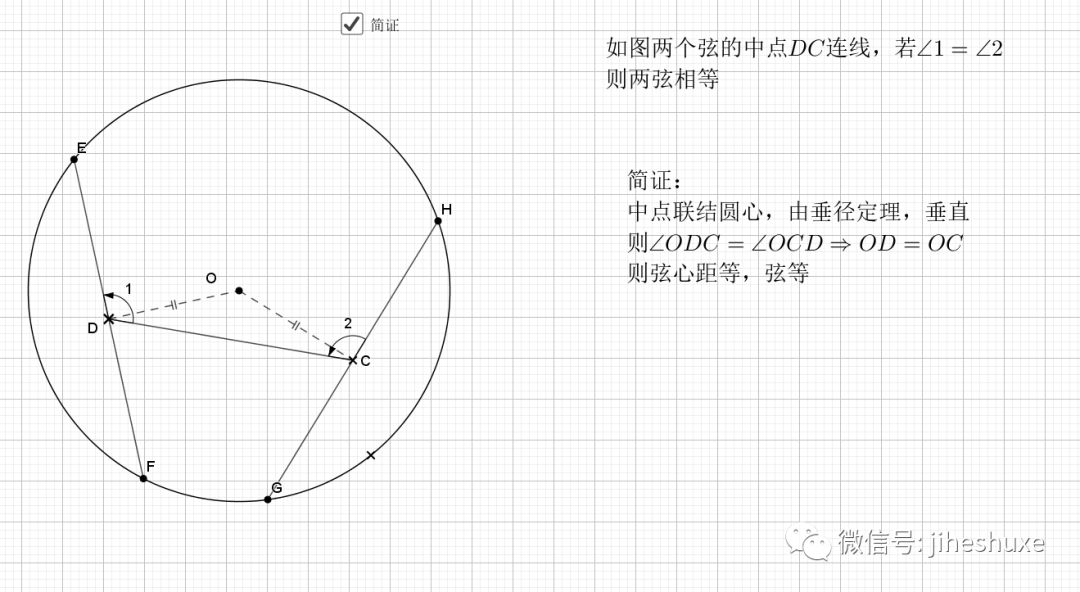
06.等弦连中点
相等的弦中点连线和两弦夹角相等,反之亦然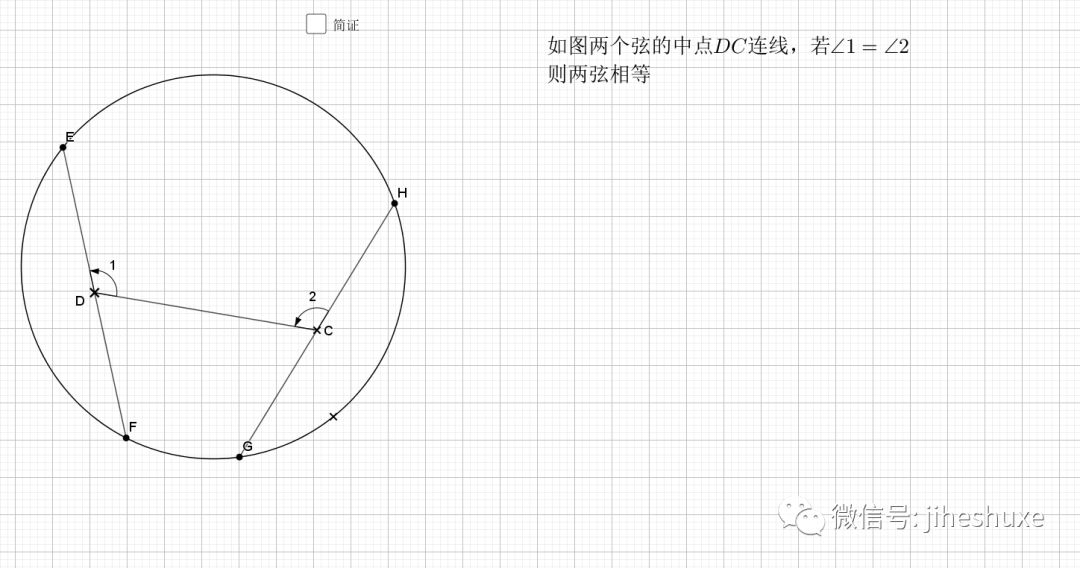
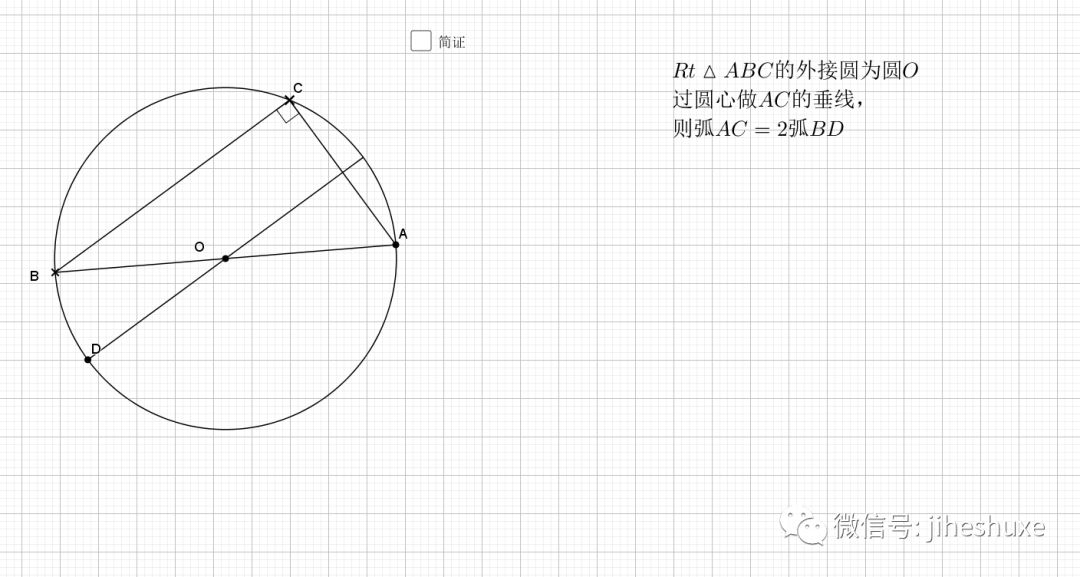
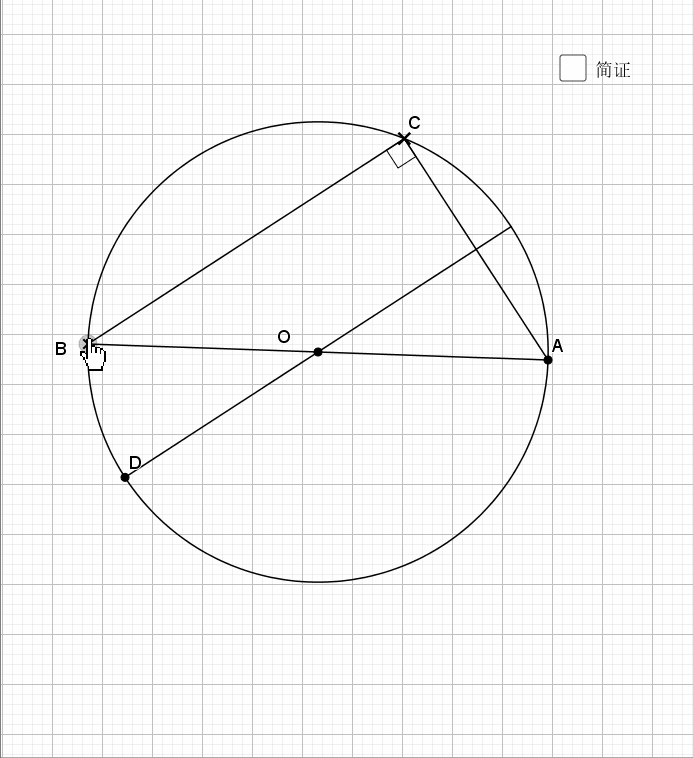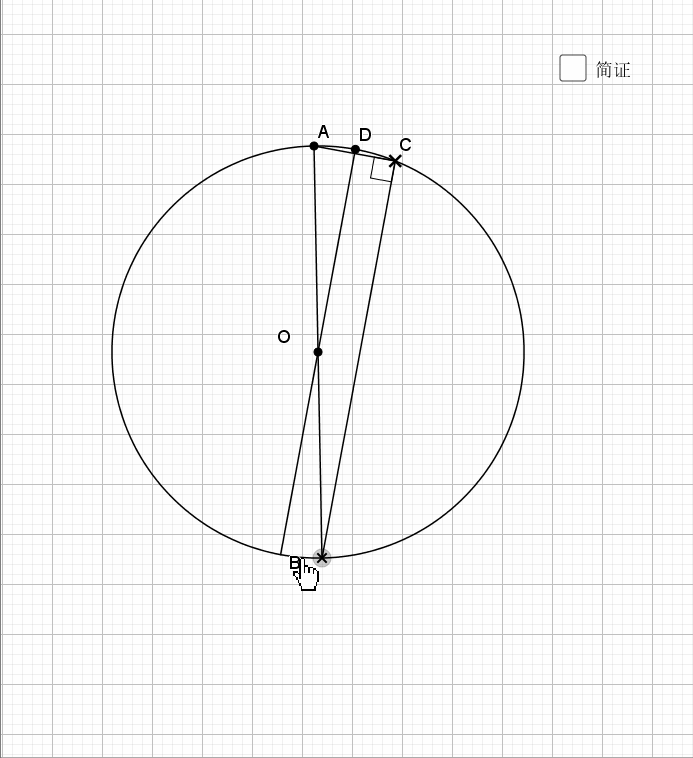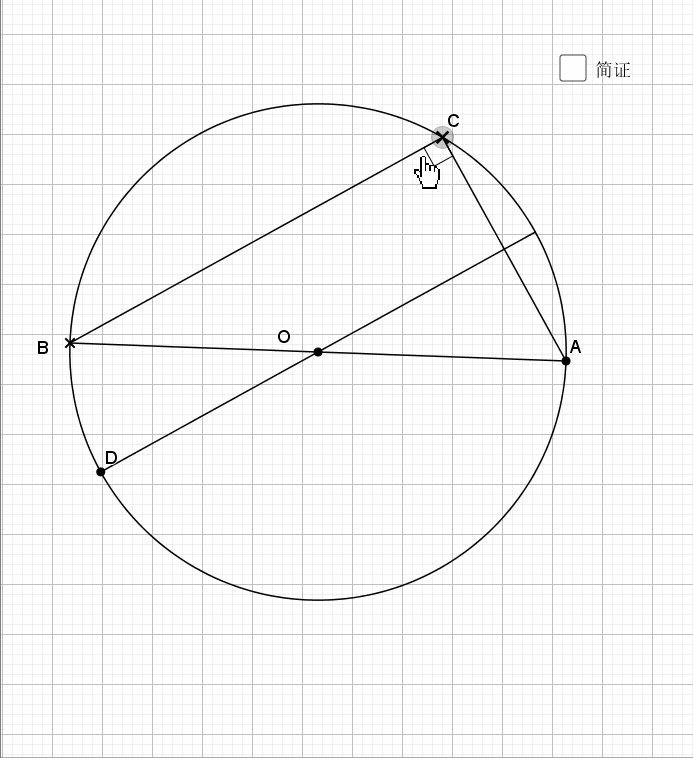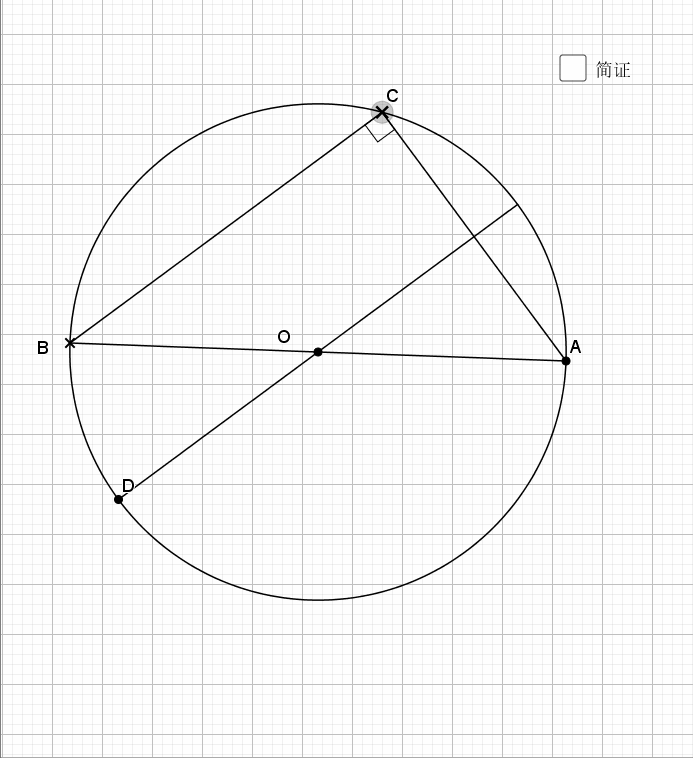
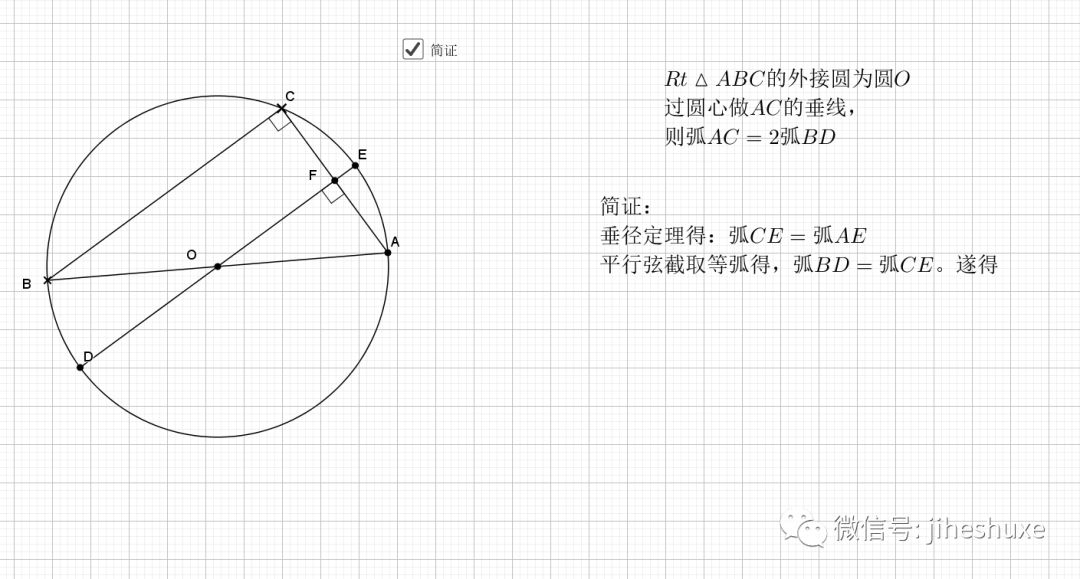
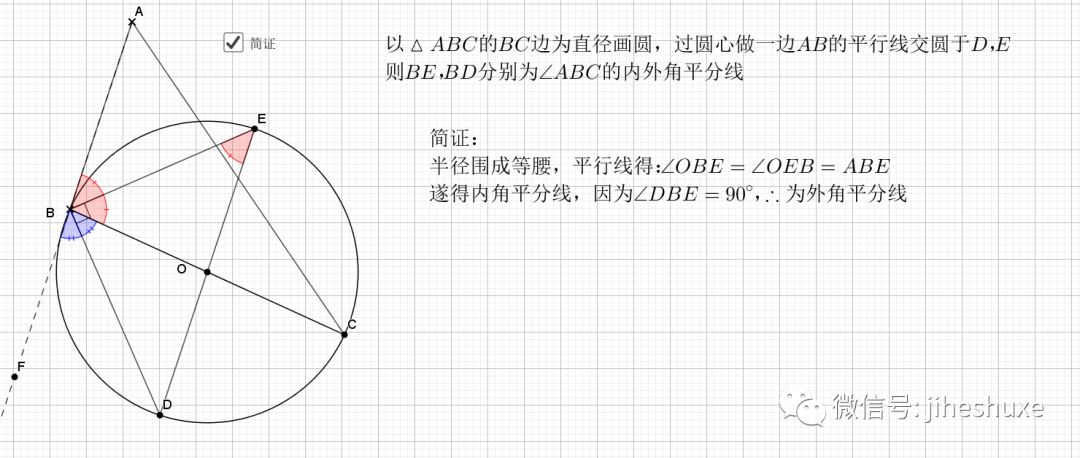
07.三角形边为直径
任何三角形以一边为直径都有如下结论
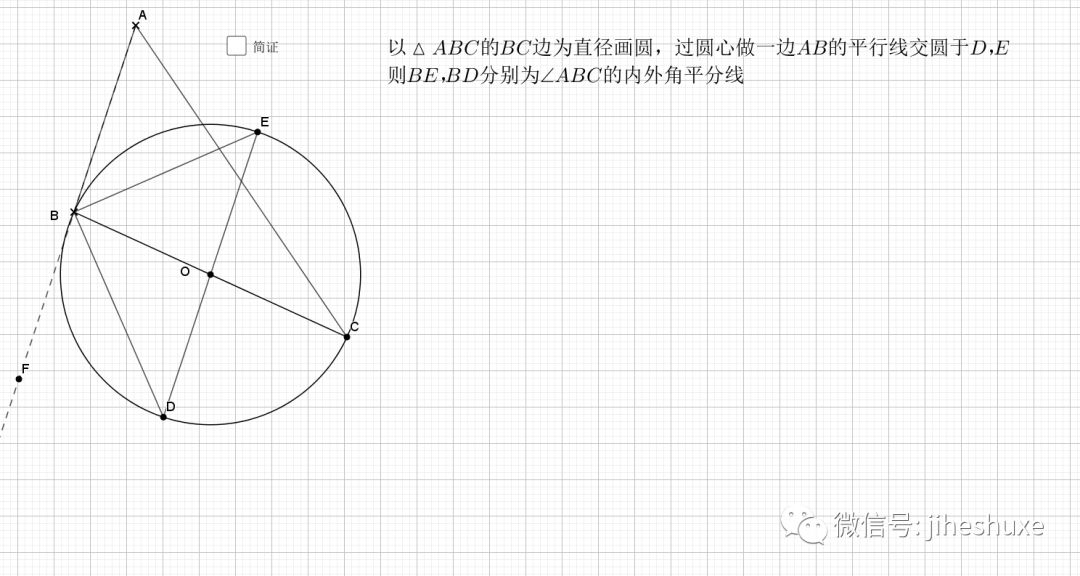
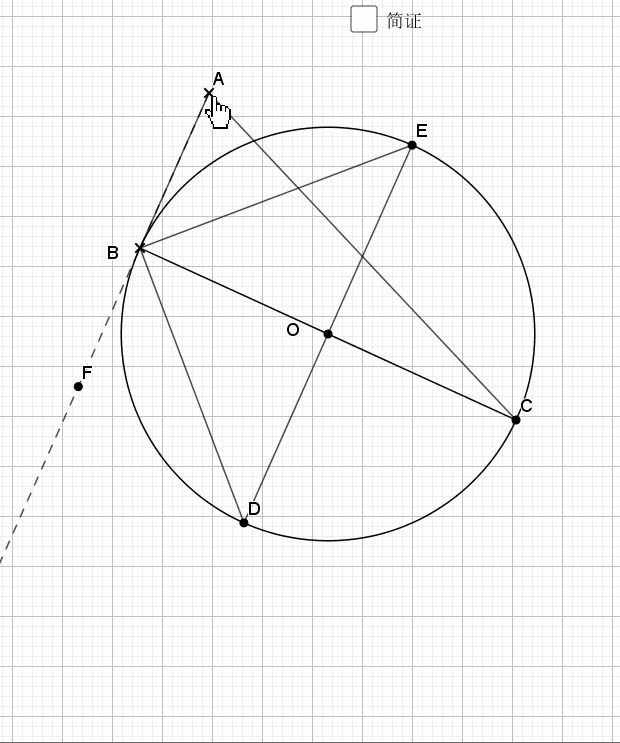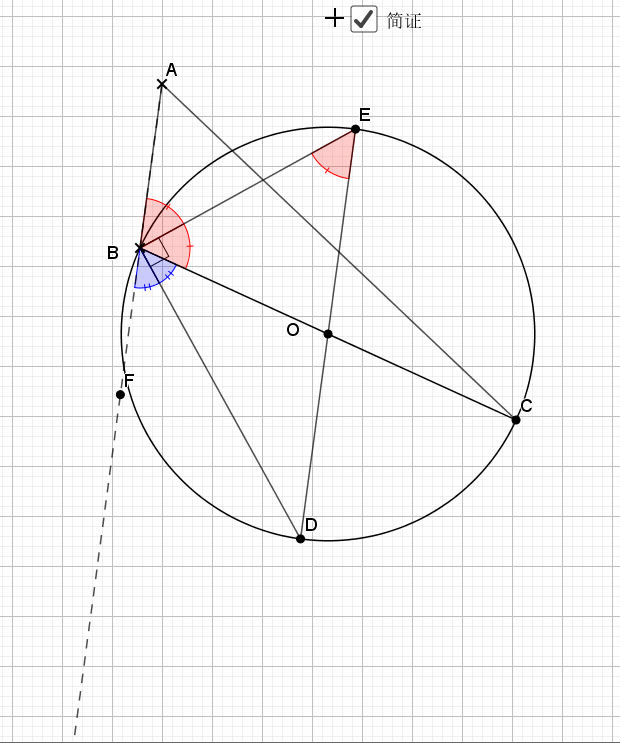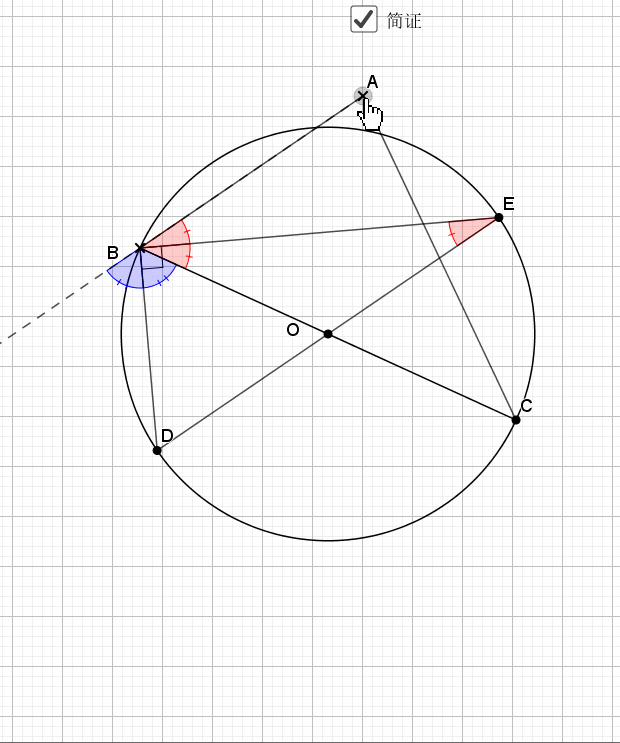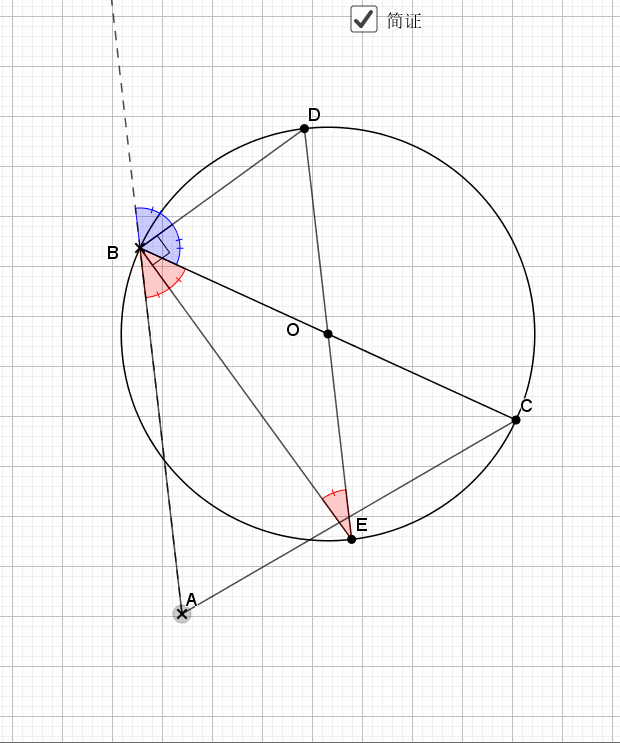
还是倒角,圆中的味道就在于倒角
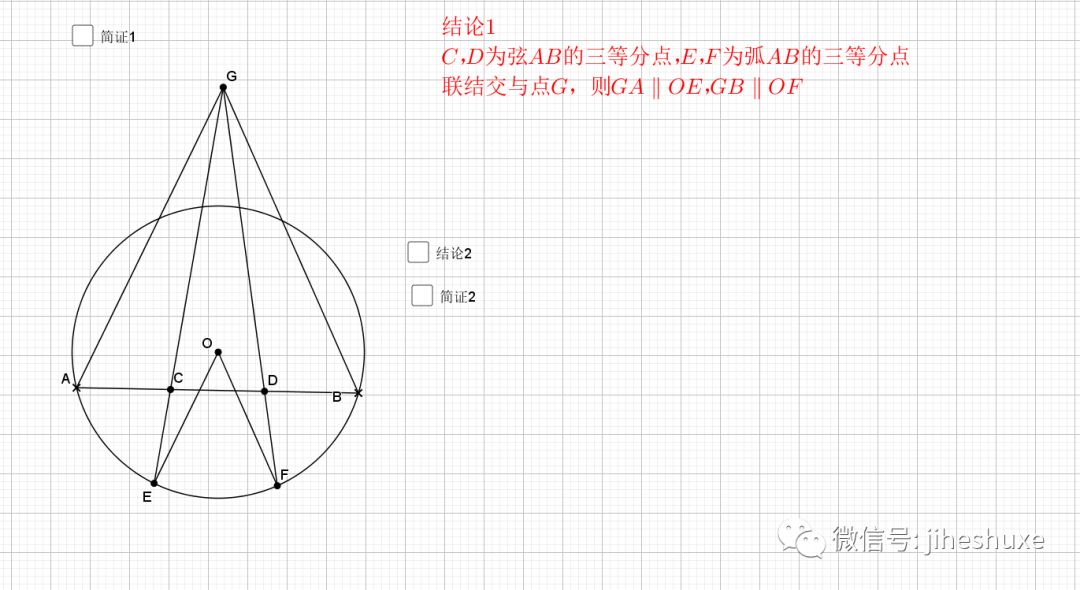
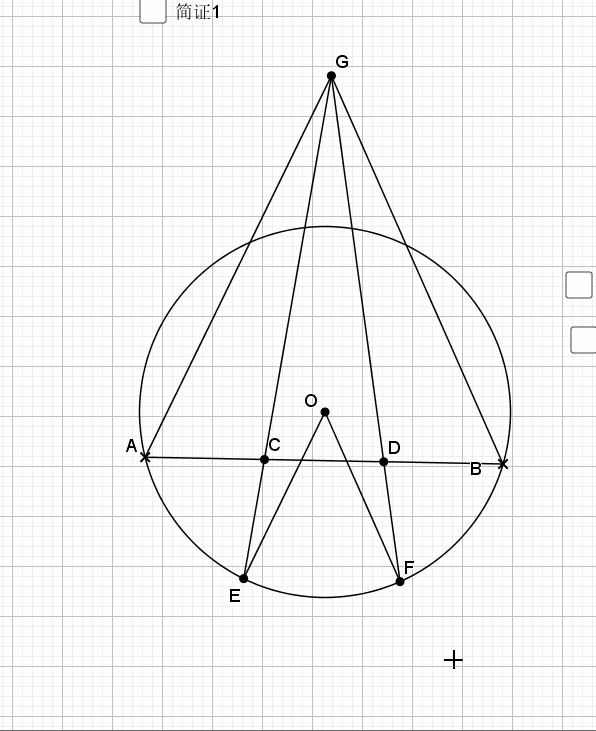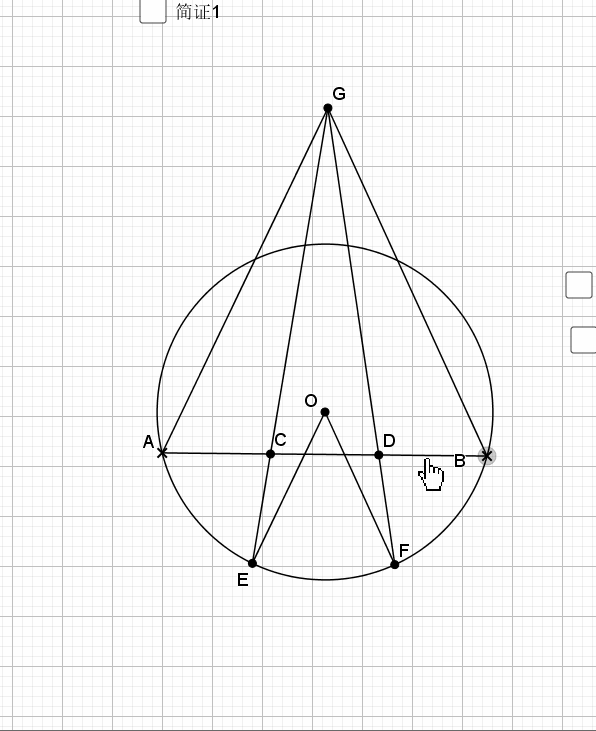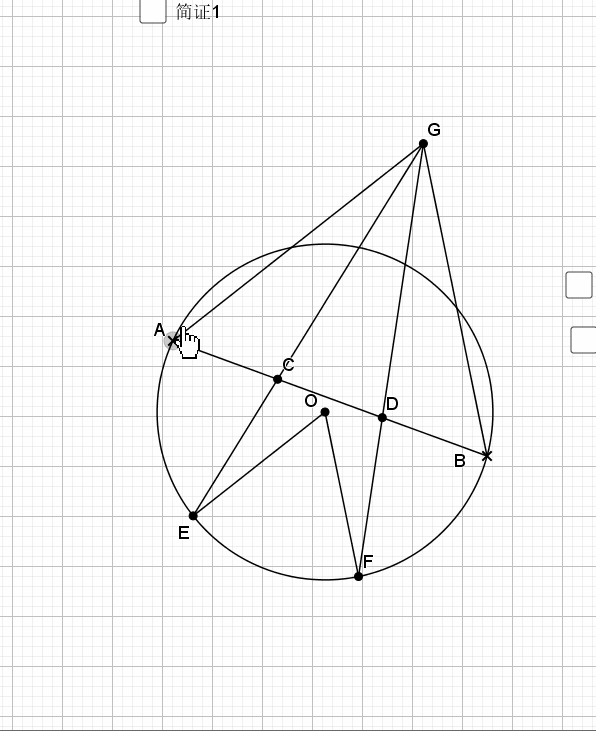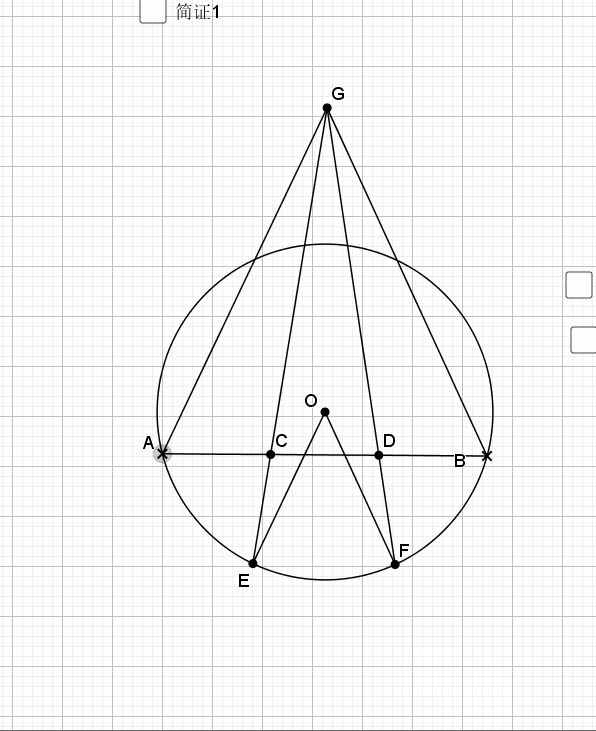
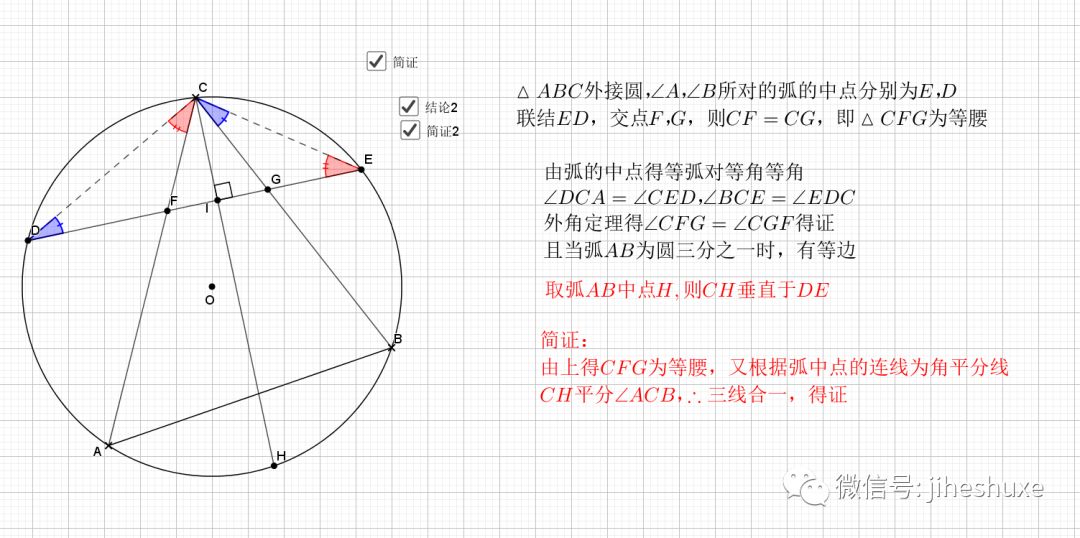
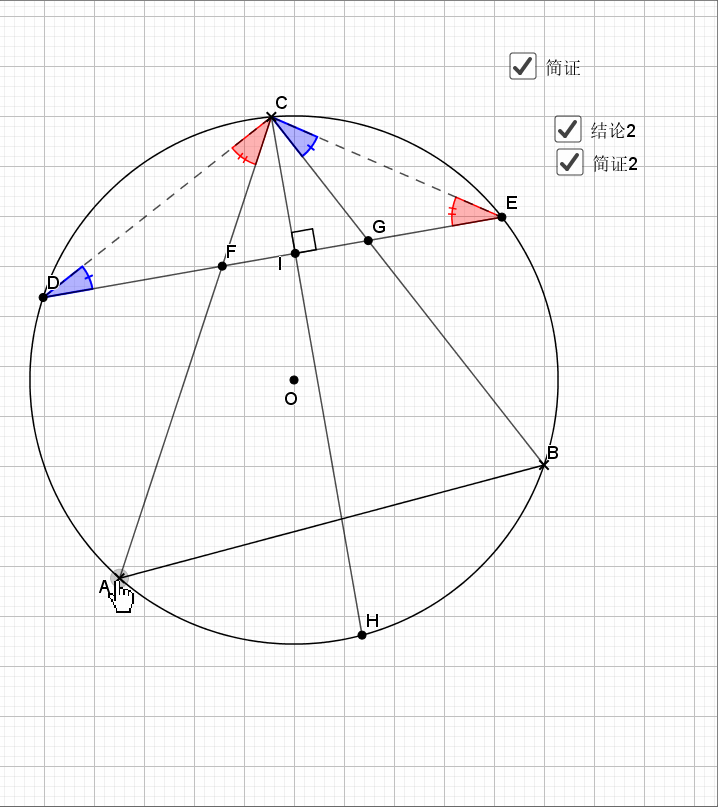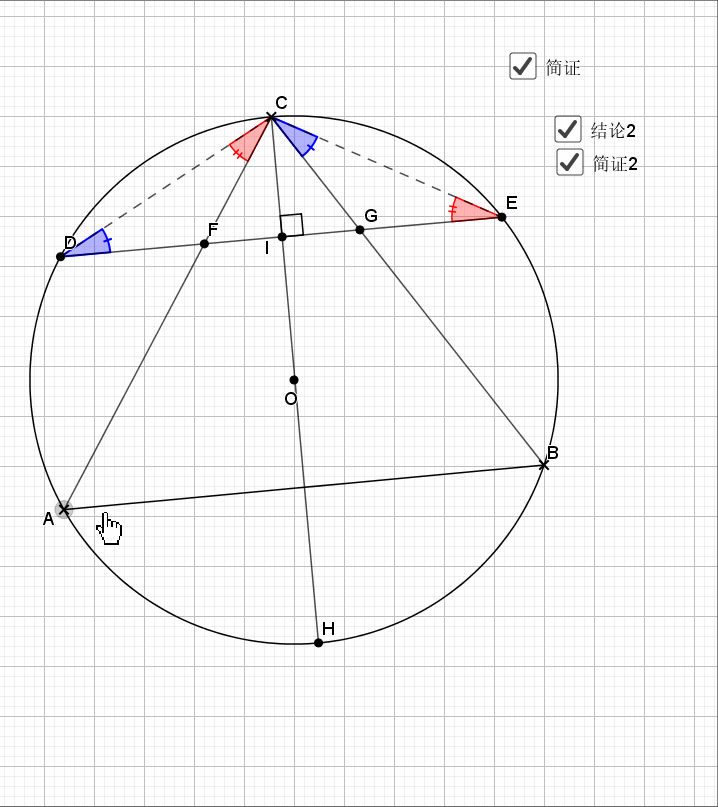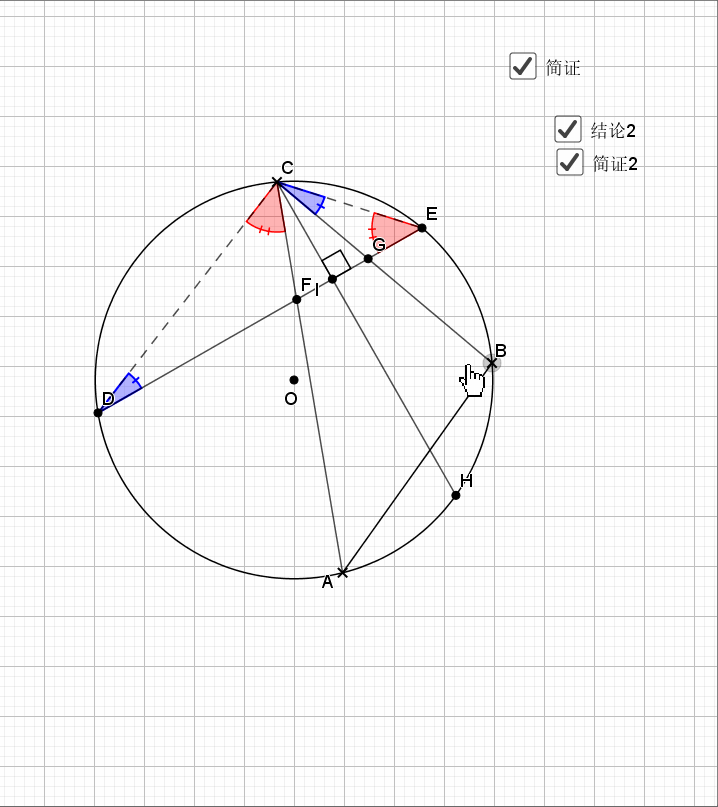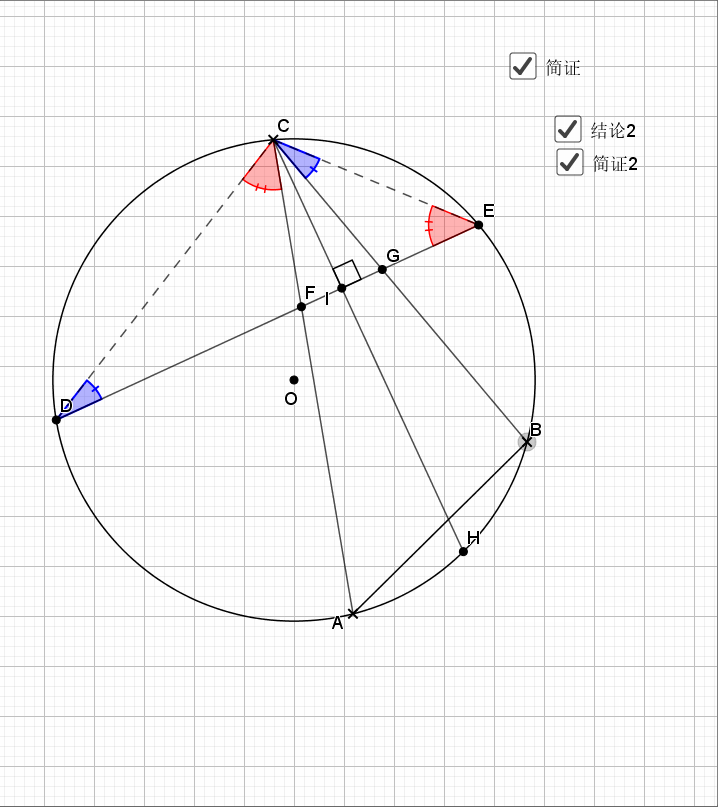
08.弦弧三等分
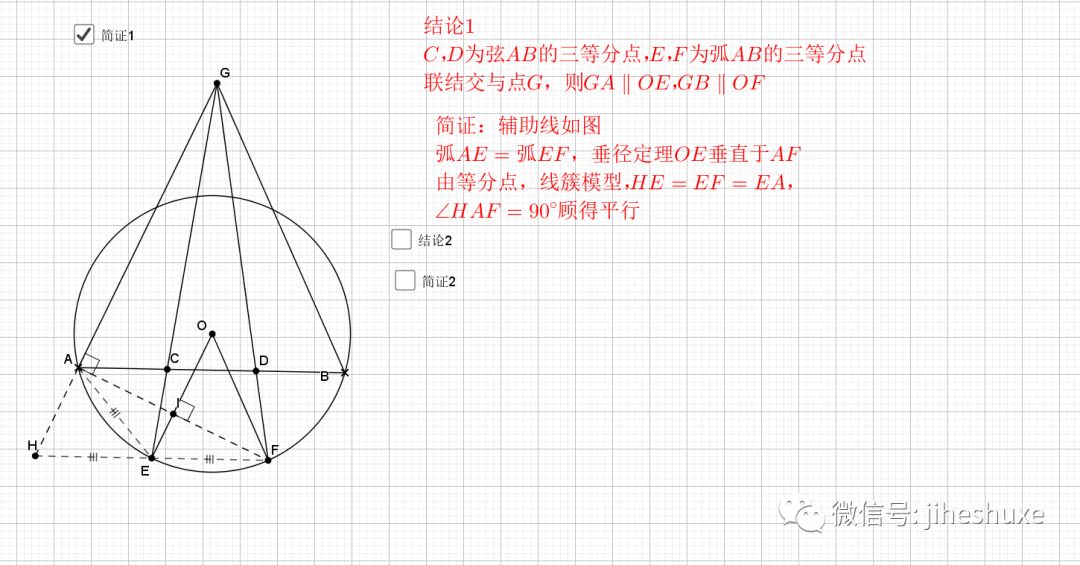
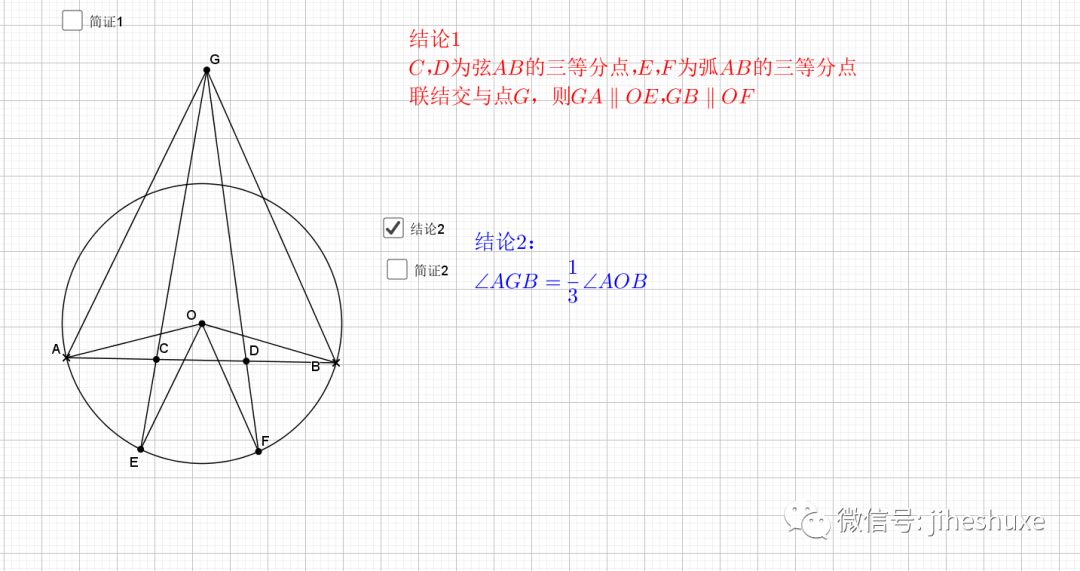
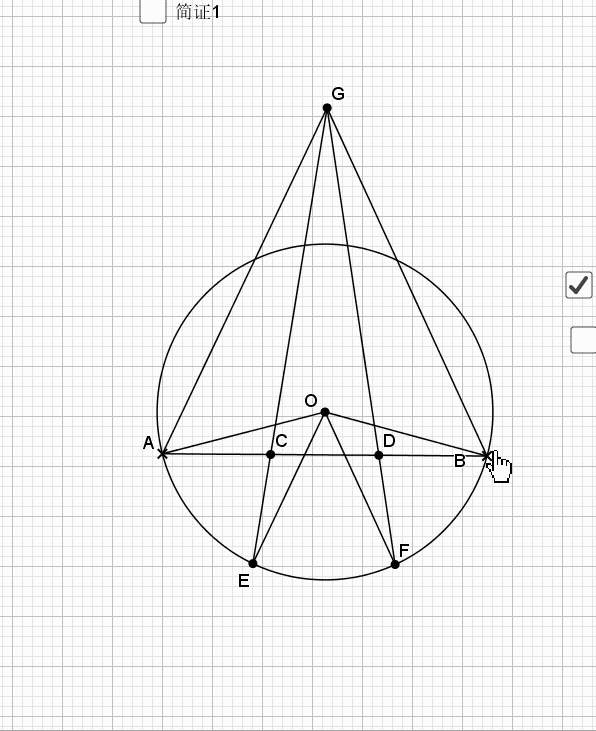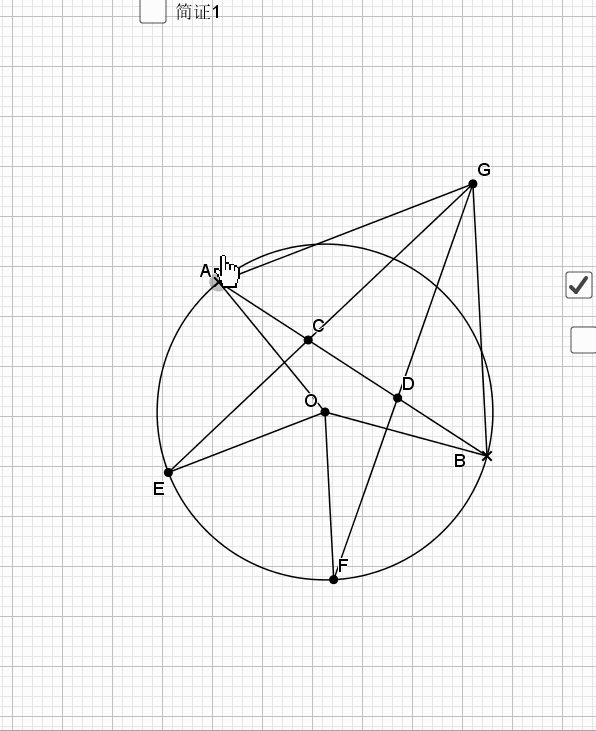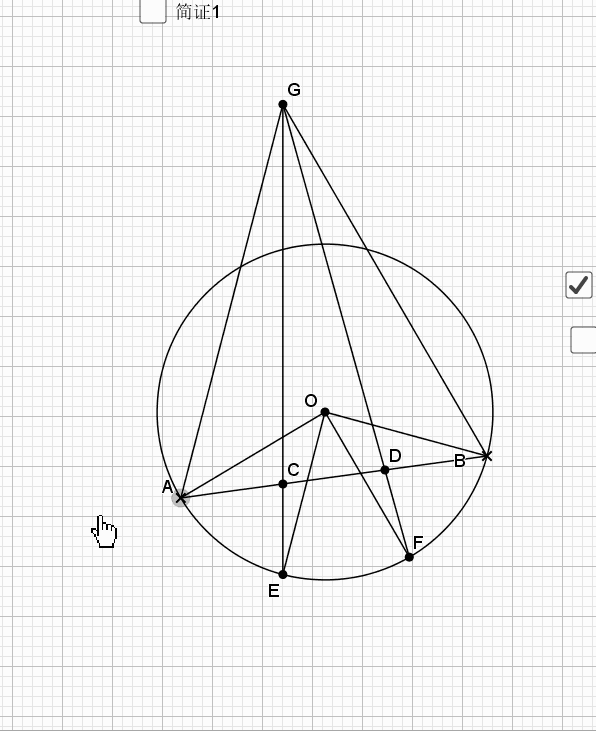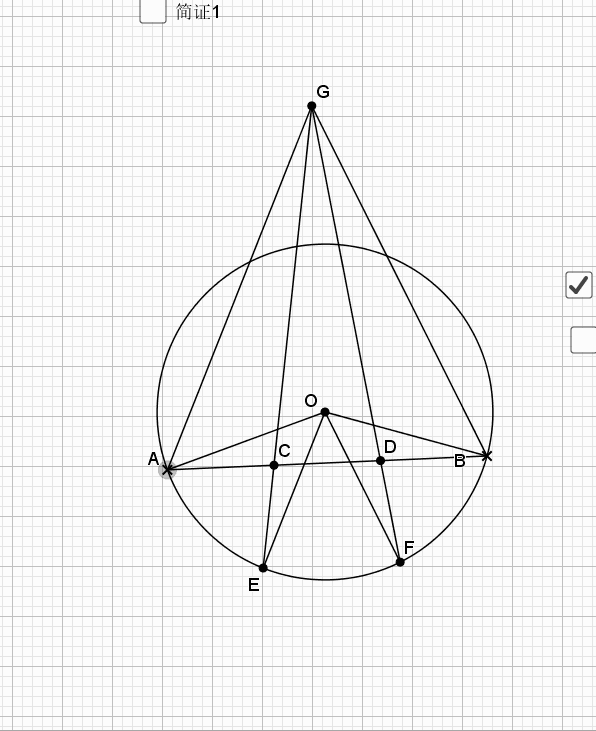
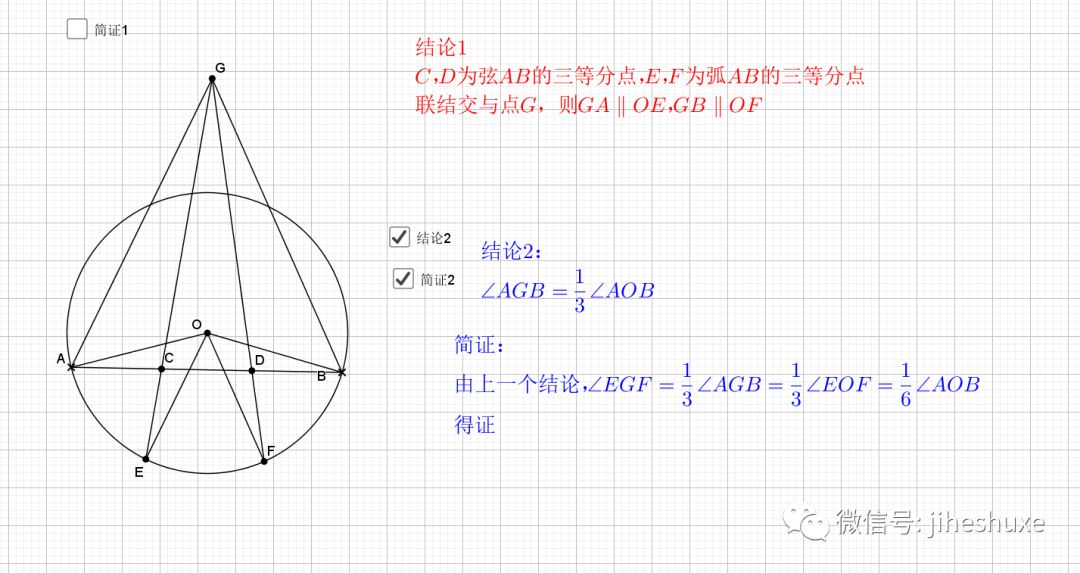
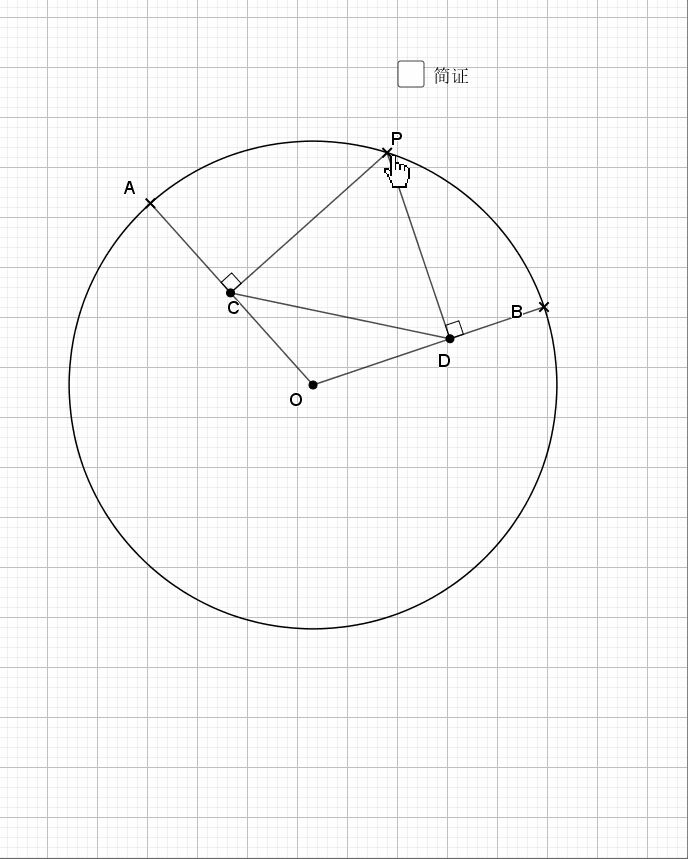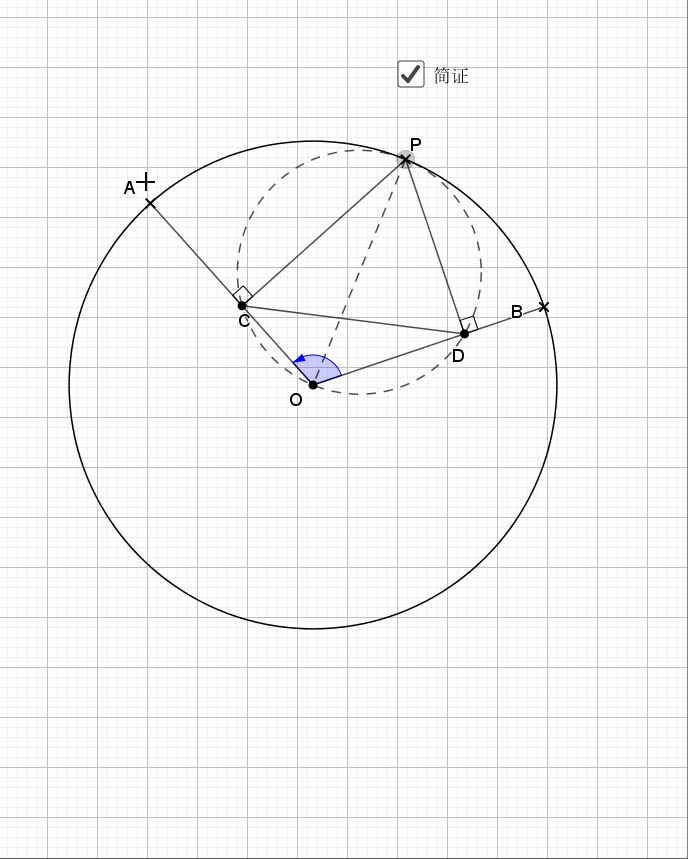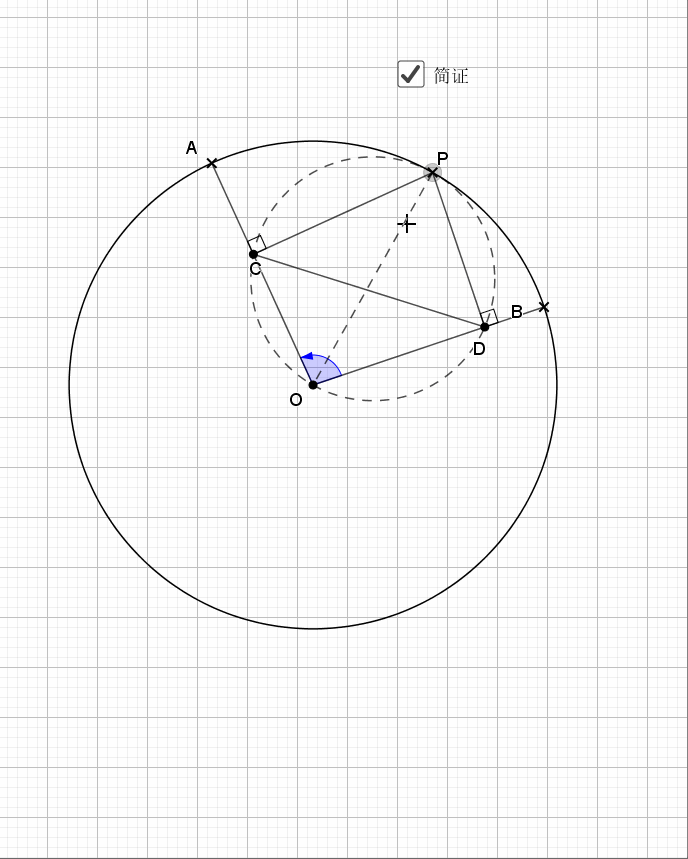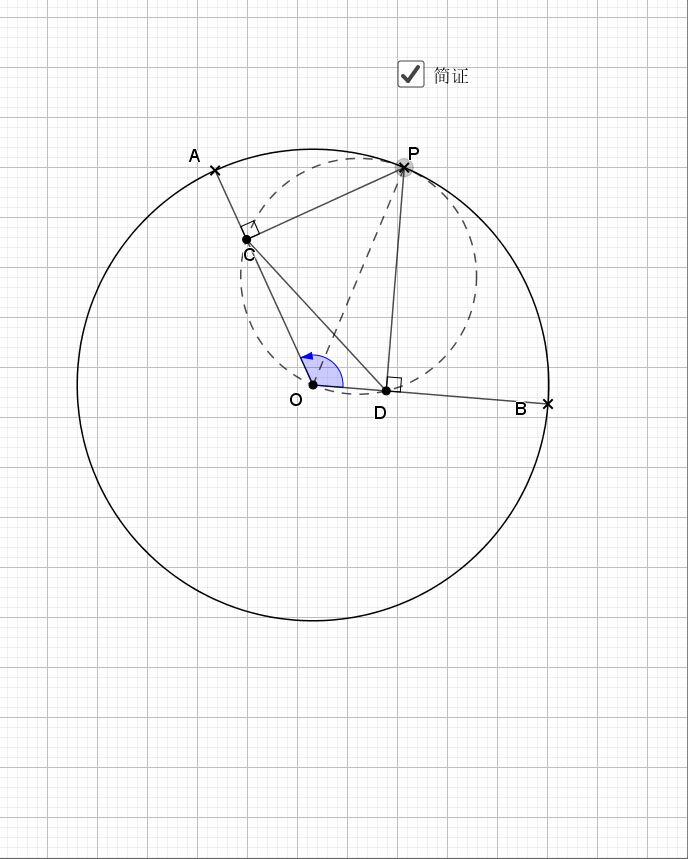
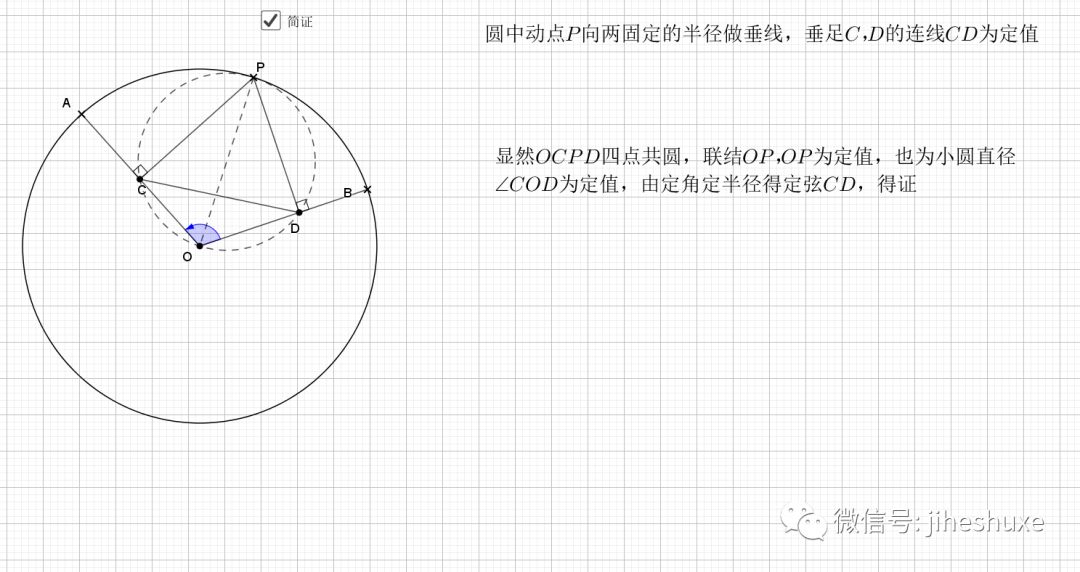
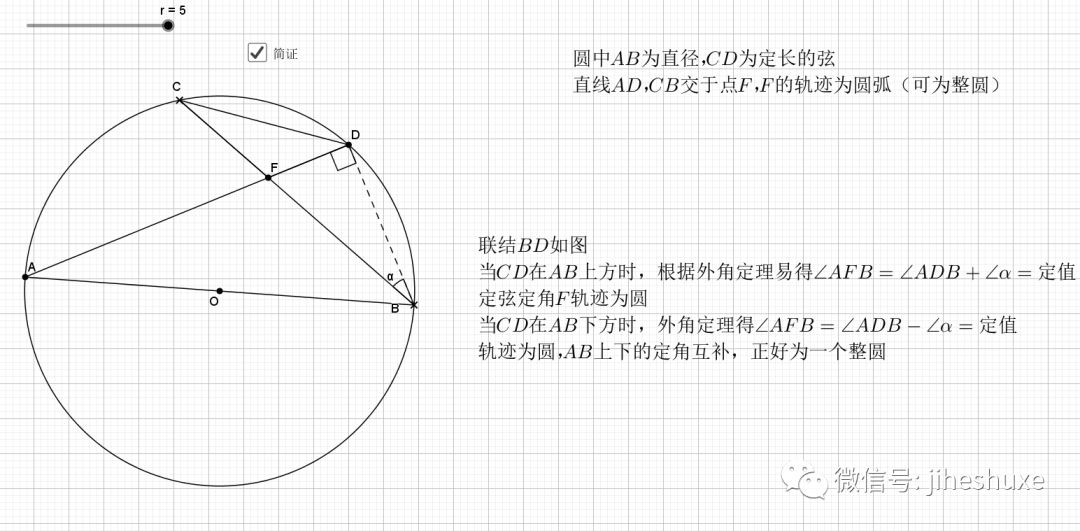
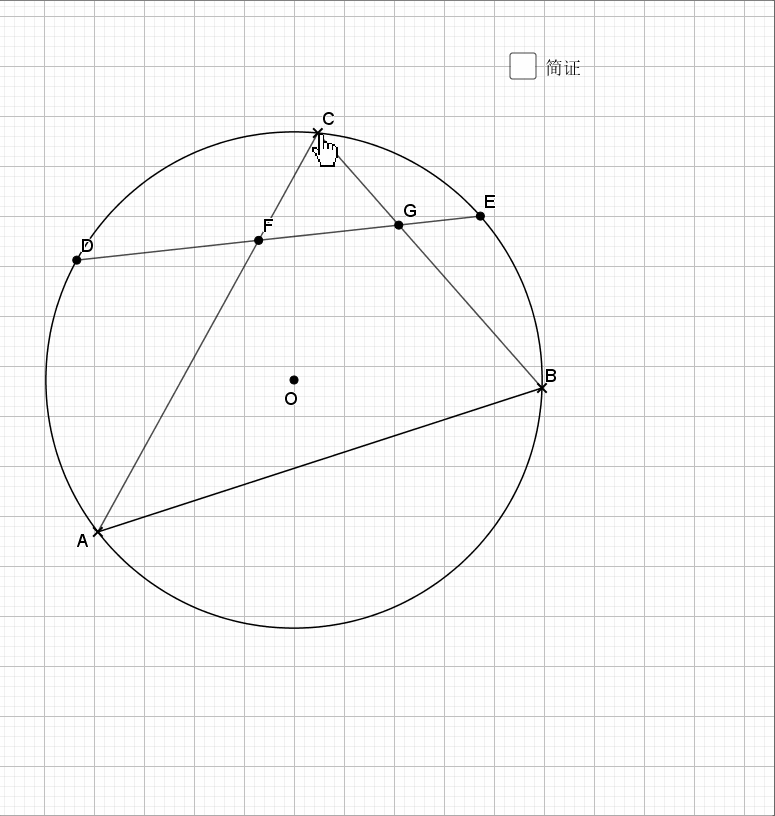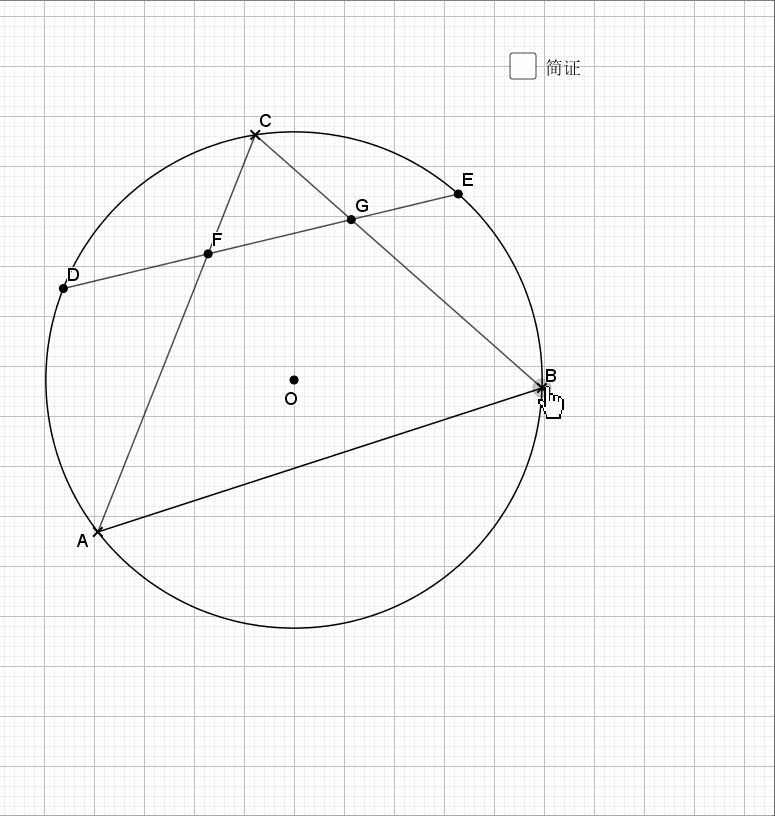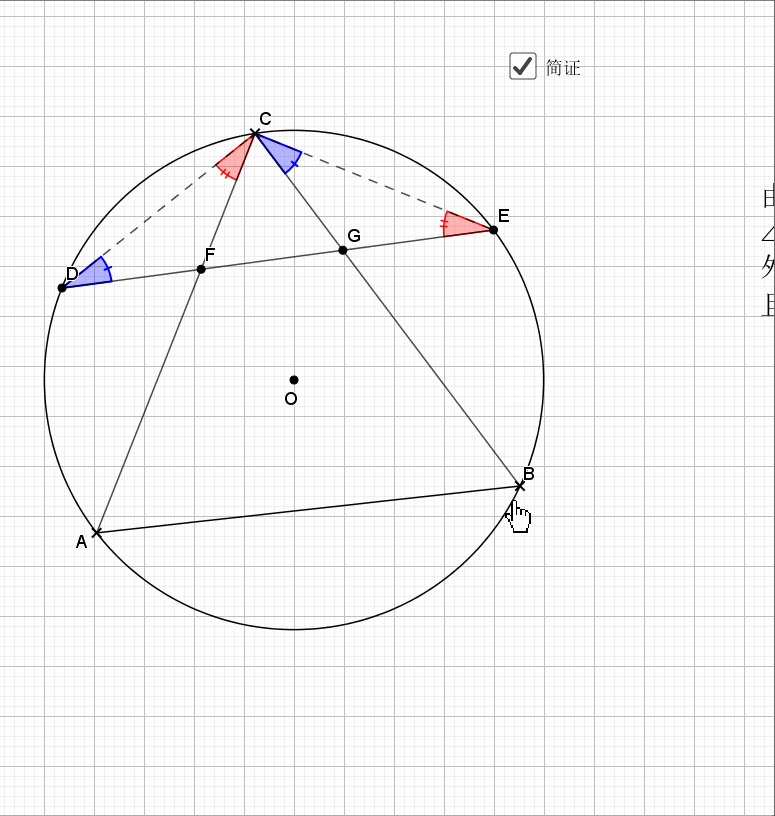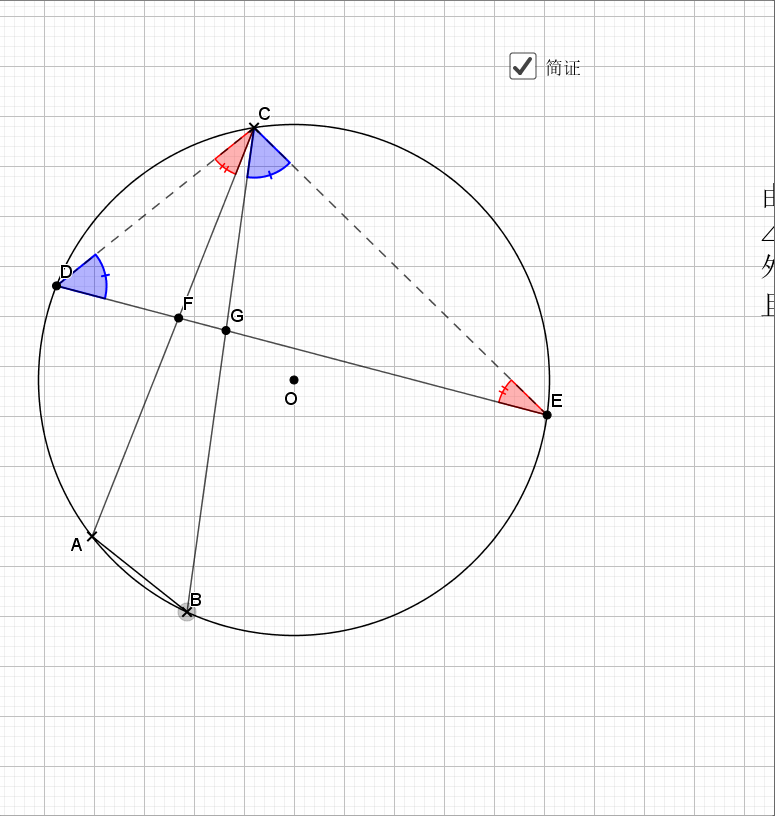
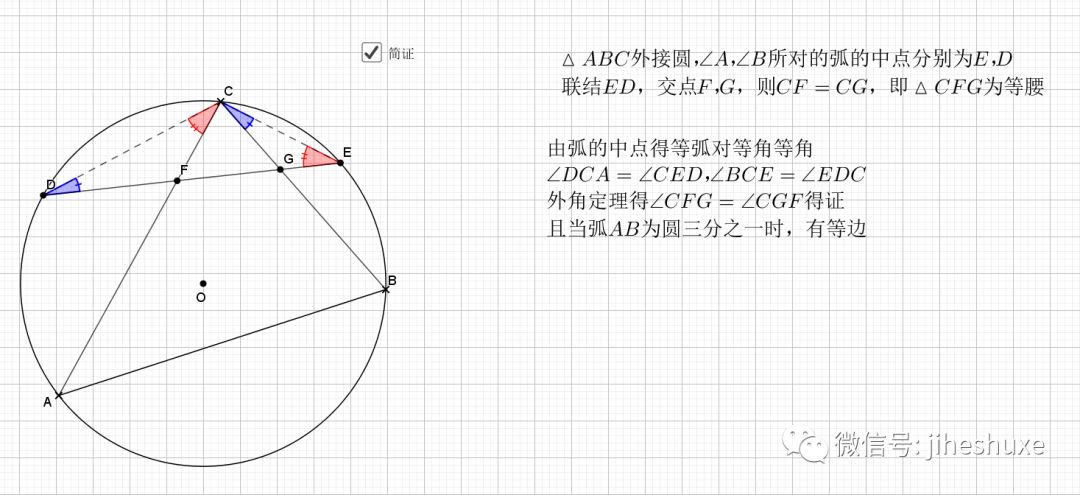
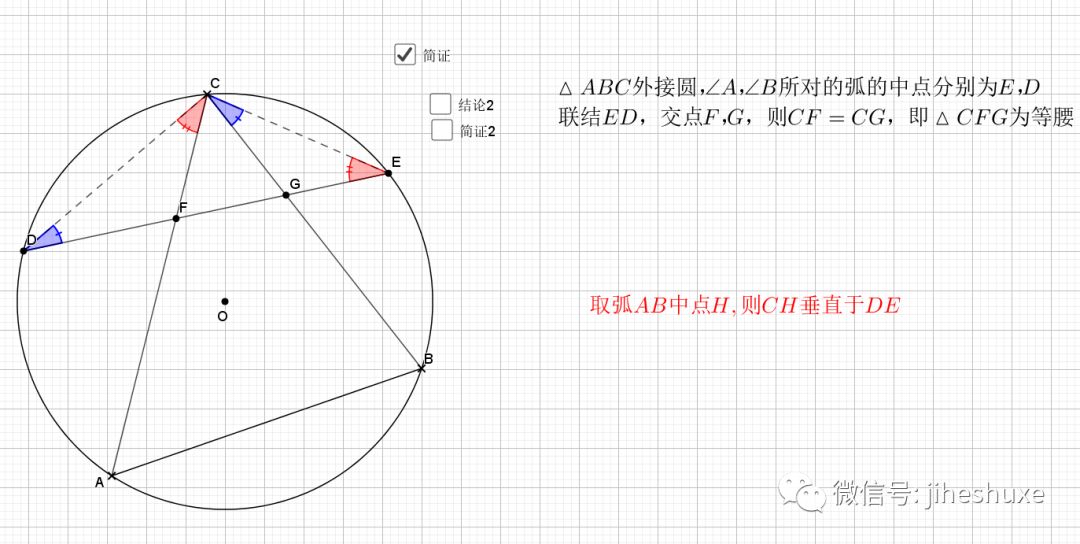
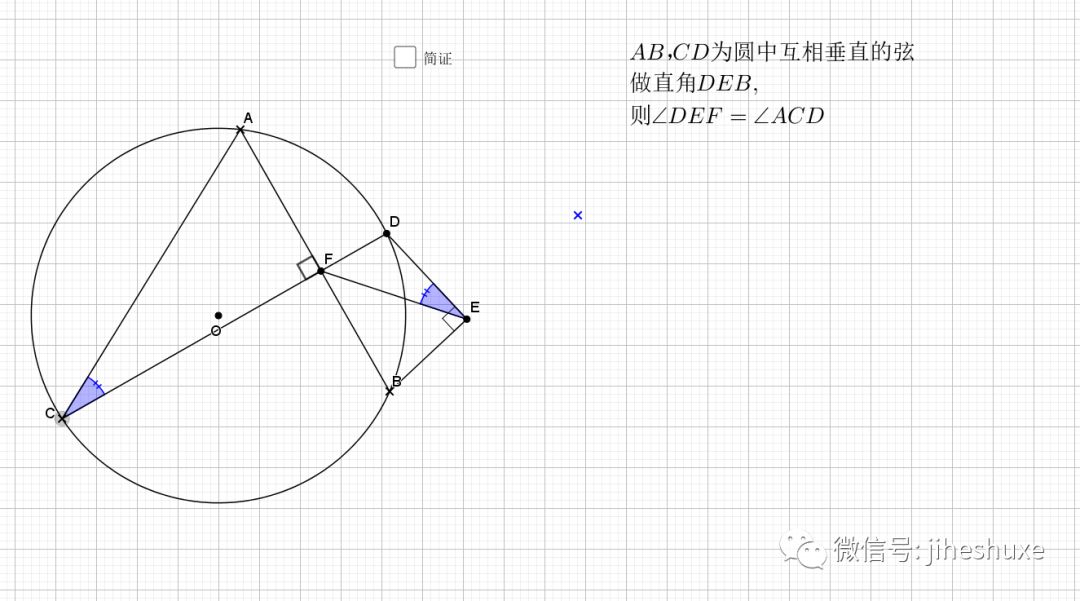
09.总是垂直
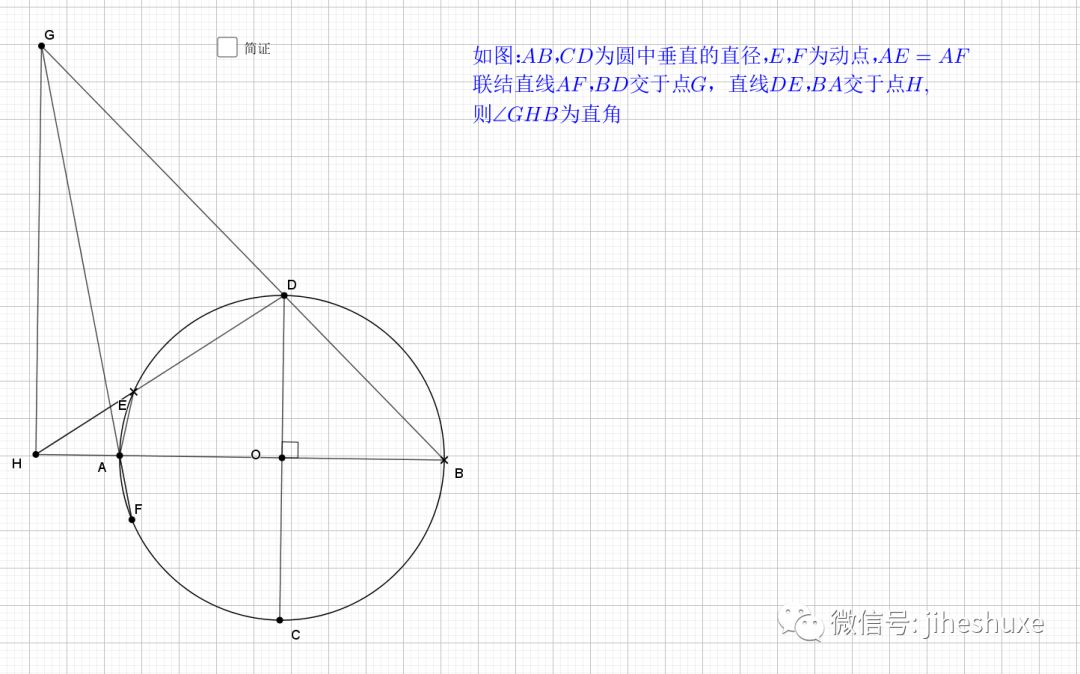
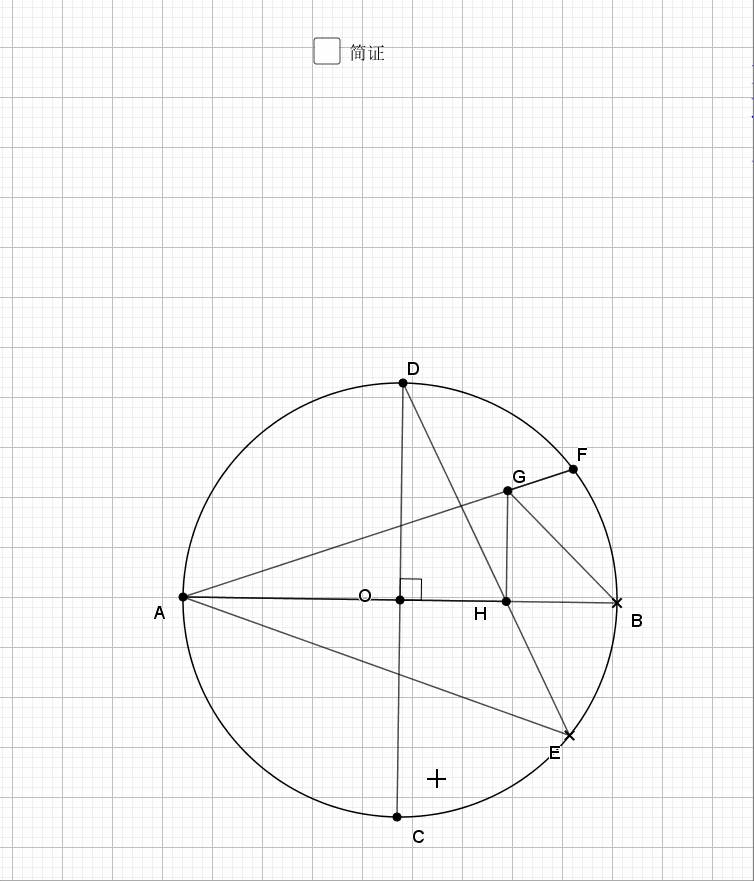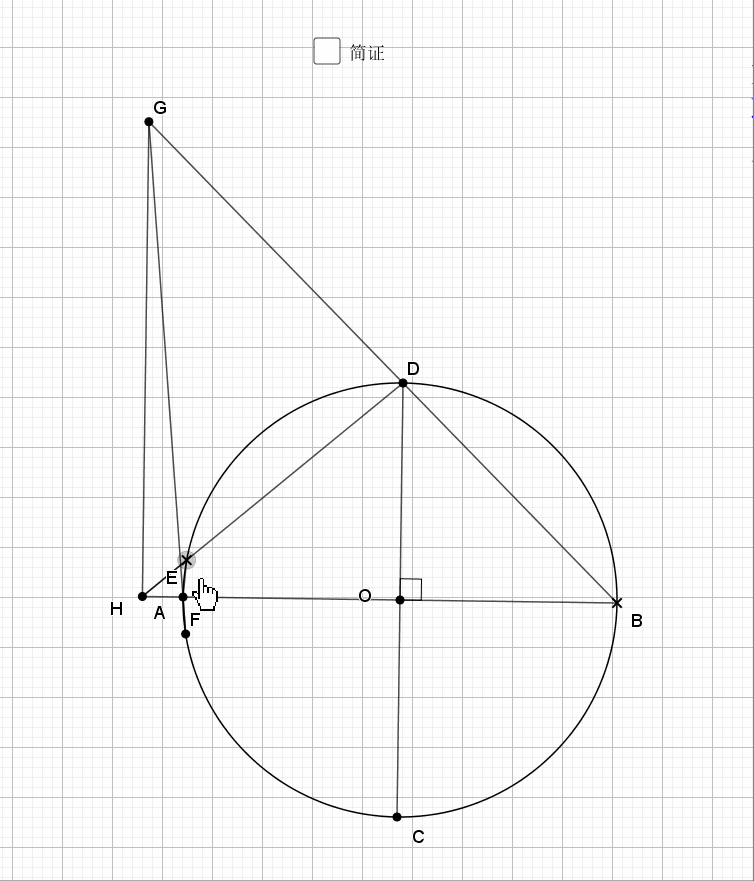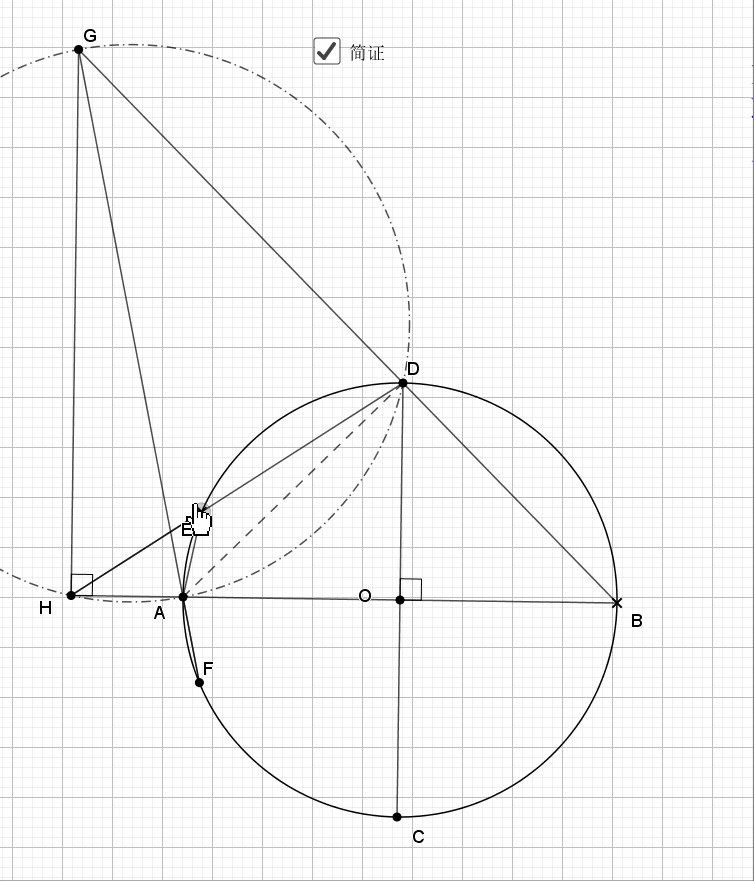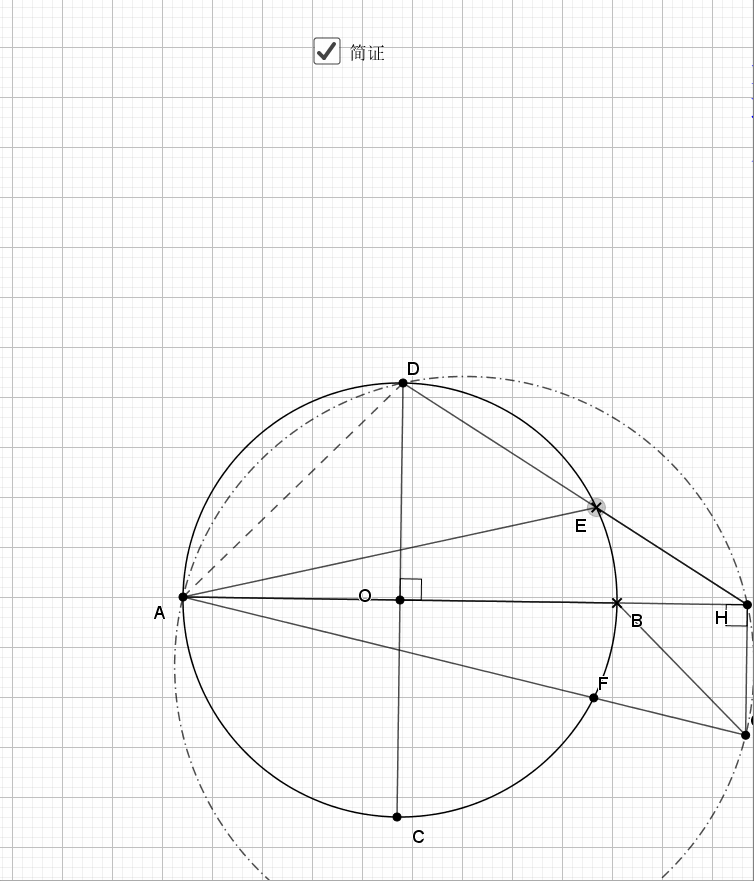
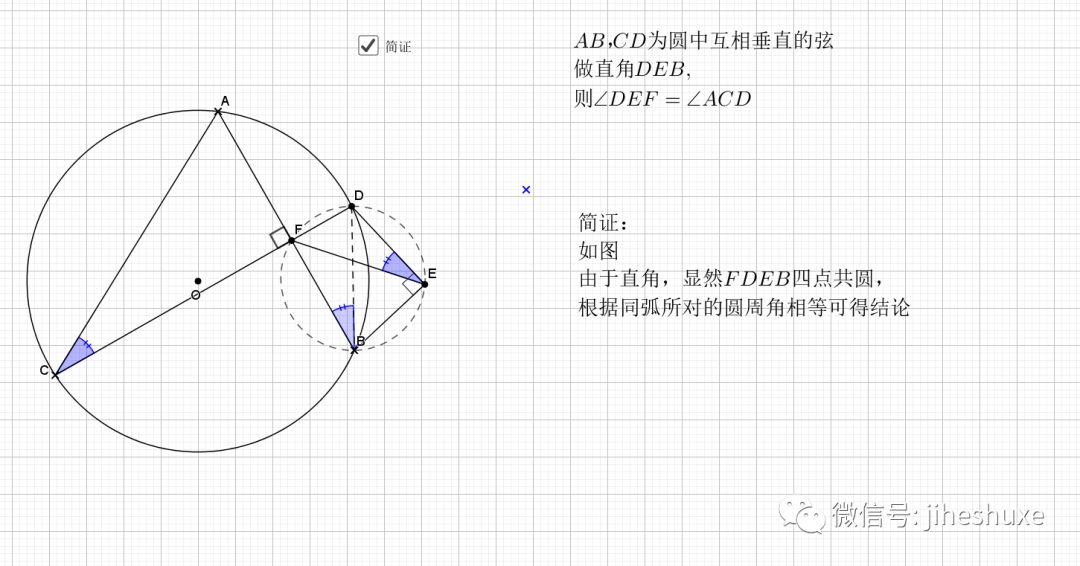
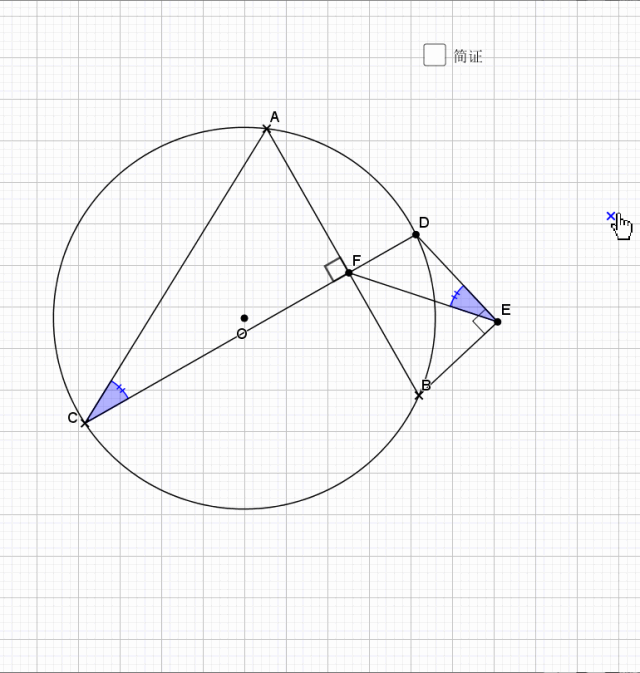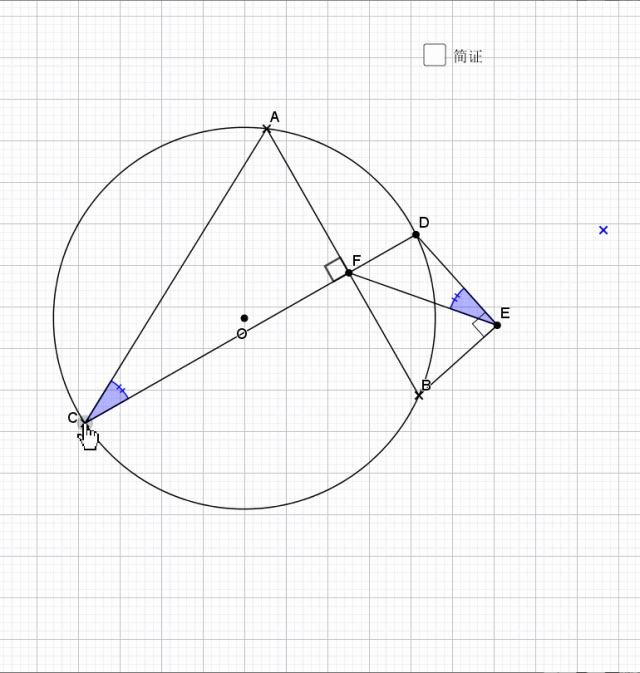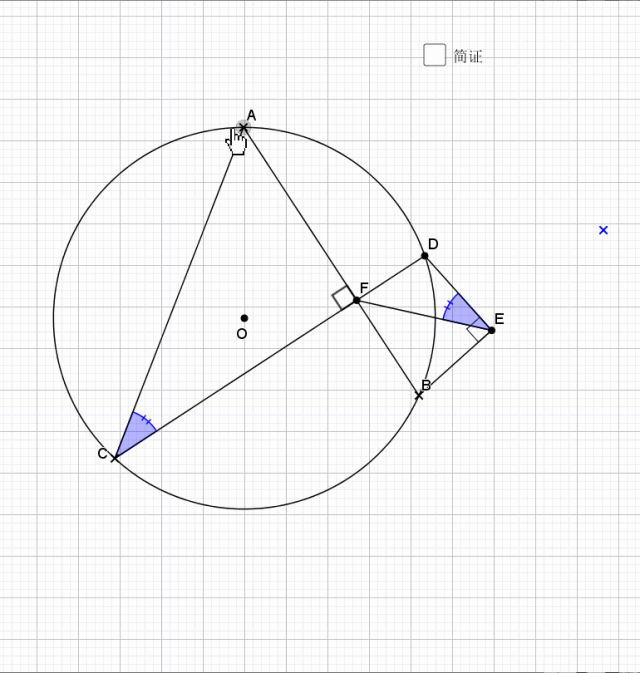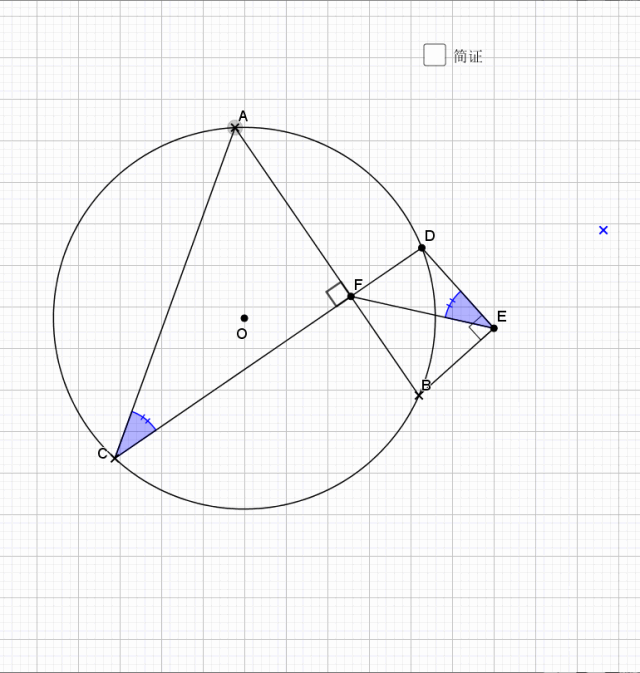
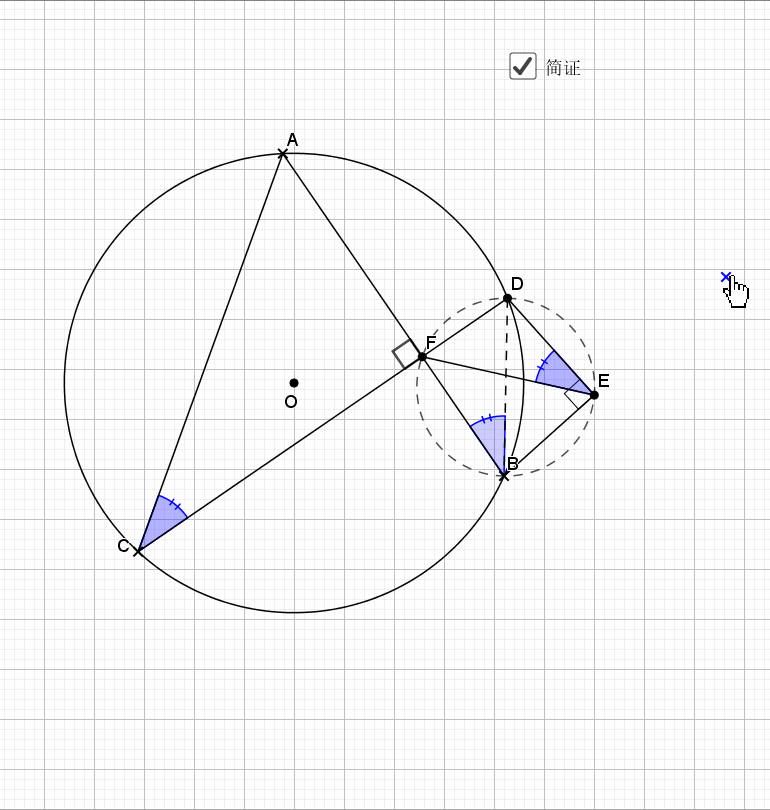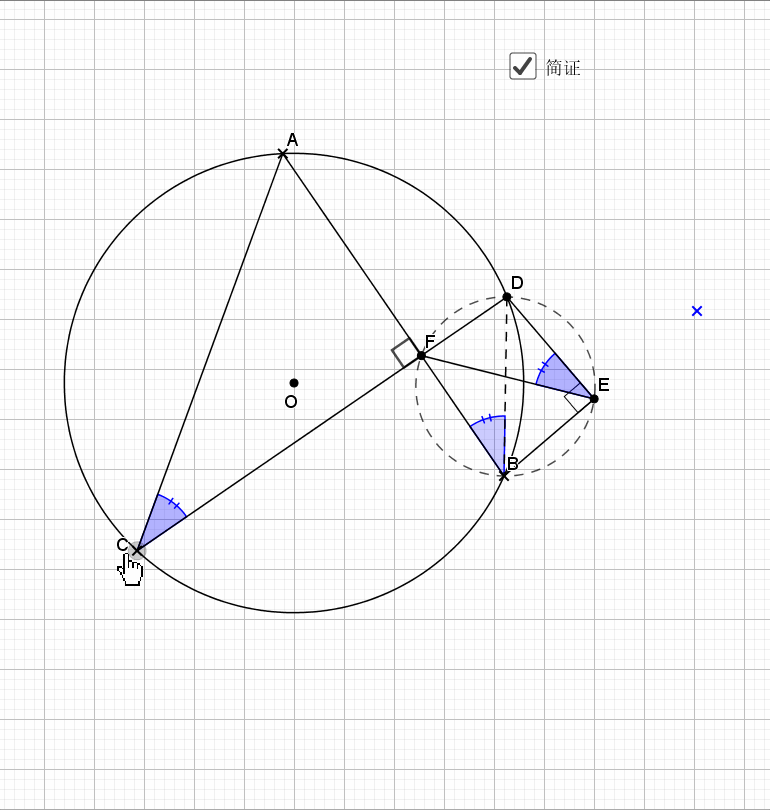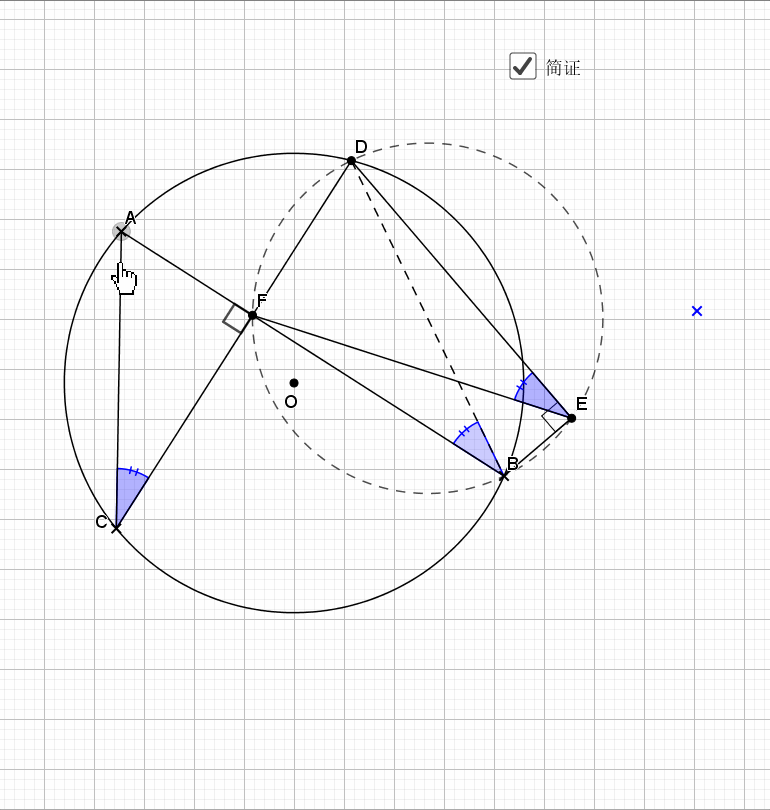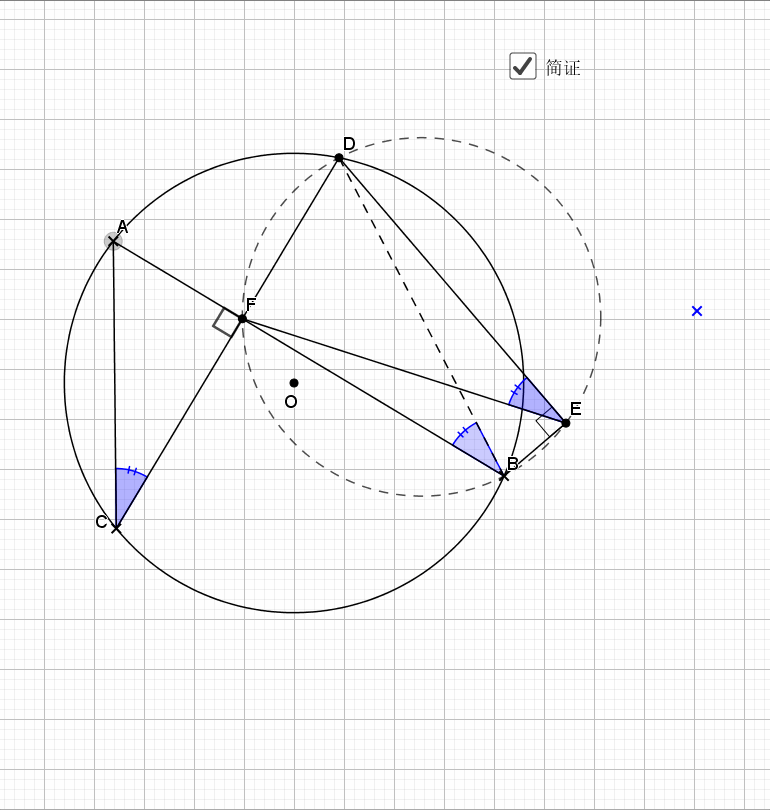
无论EF在什么位置,垂直都是成立的
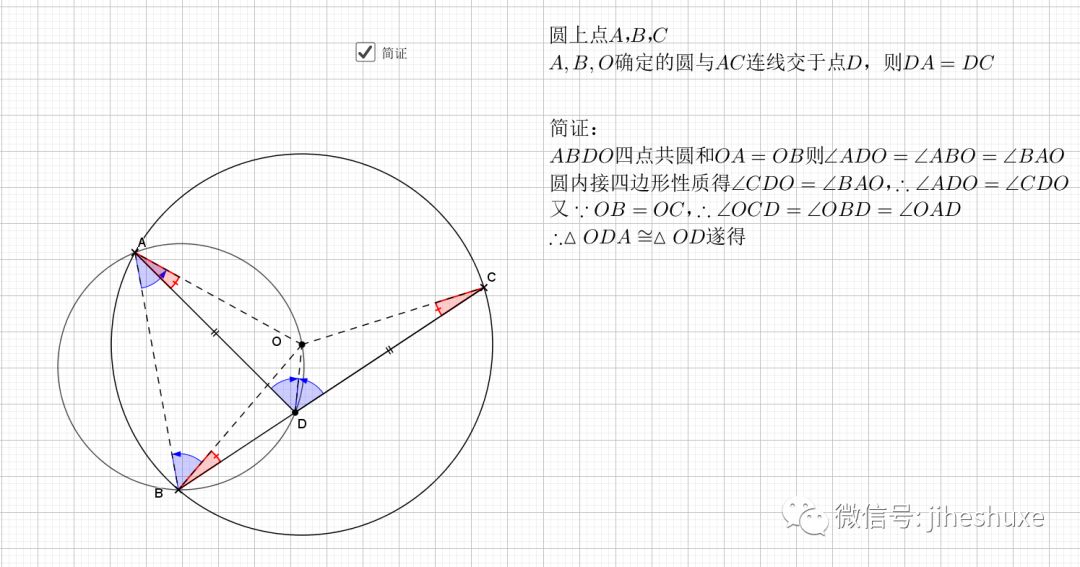
证明主要利用了圆内接四边形的性质,还有四点共圆的证明
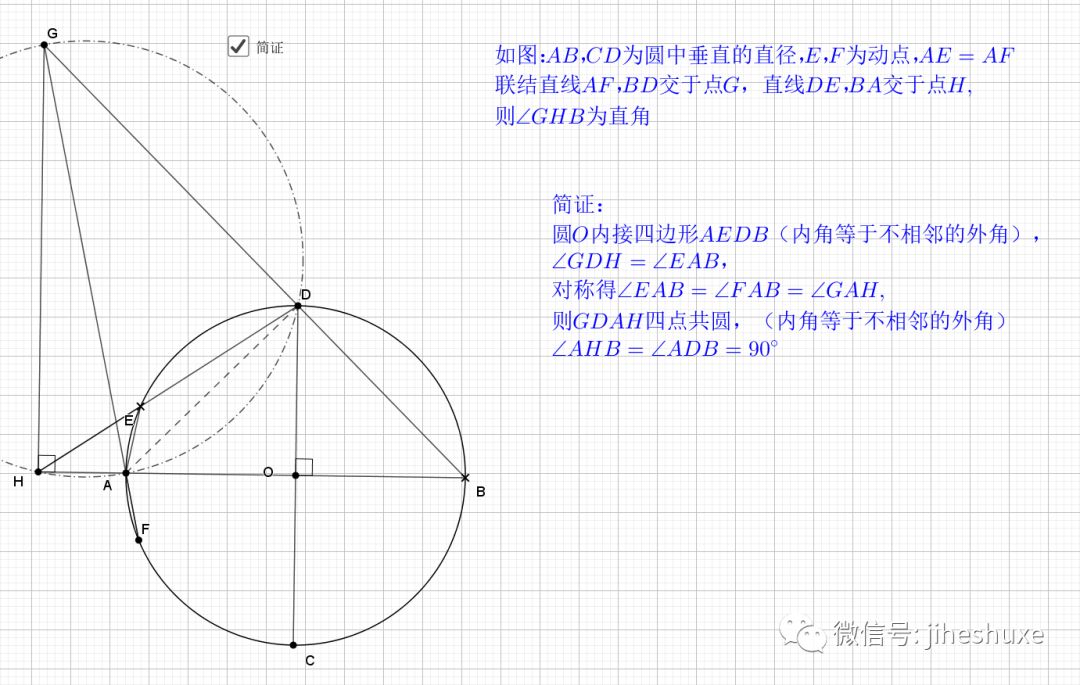
平行的弦夹等弧都知道,这是平行弦得四点共圆
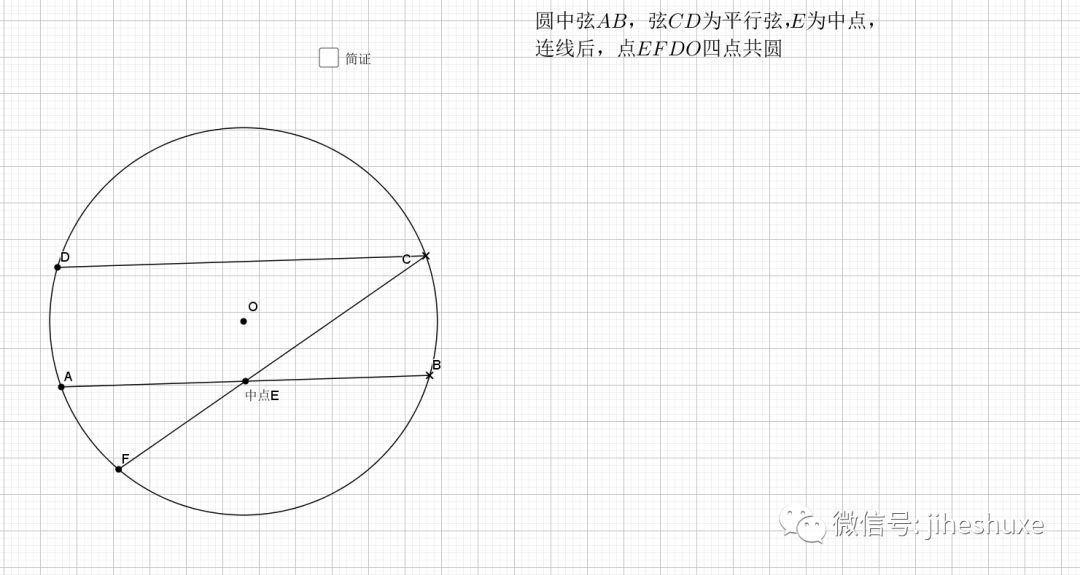
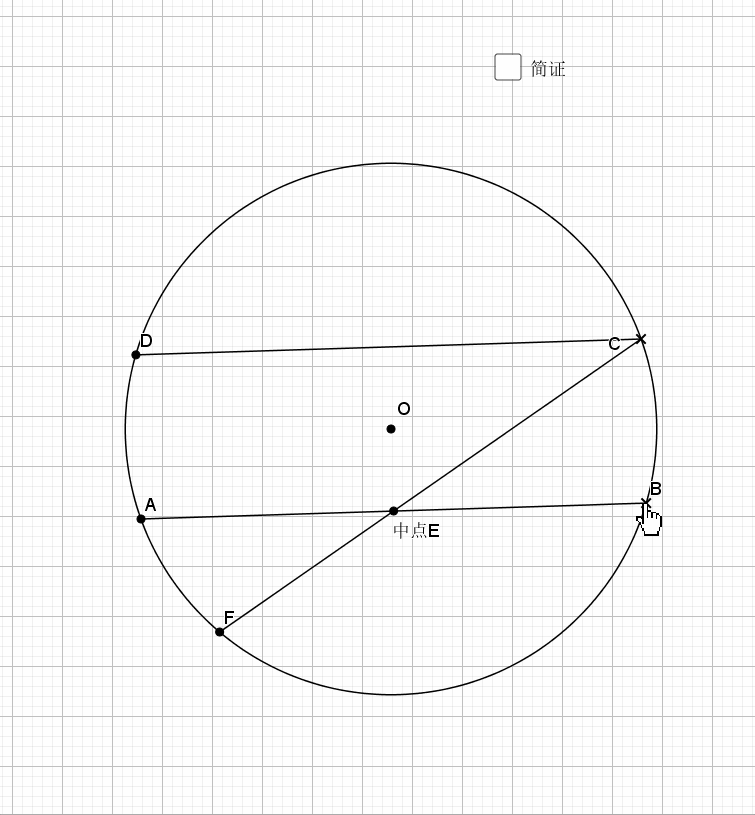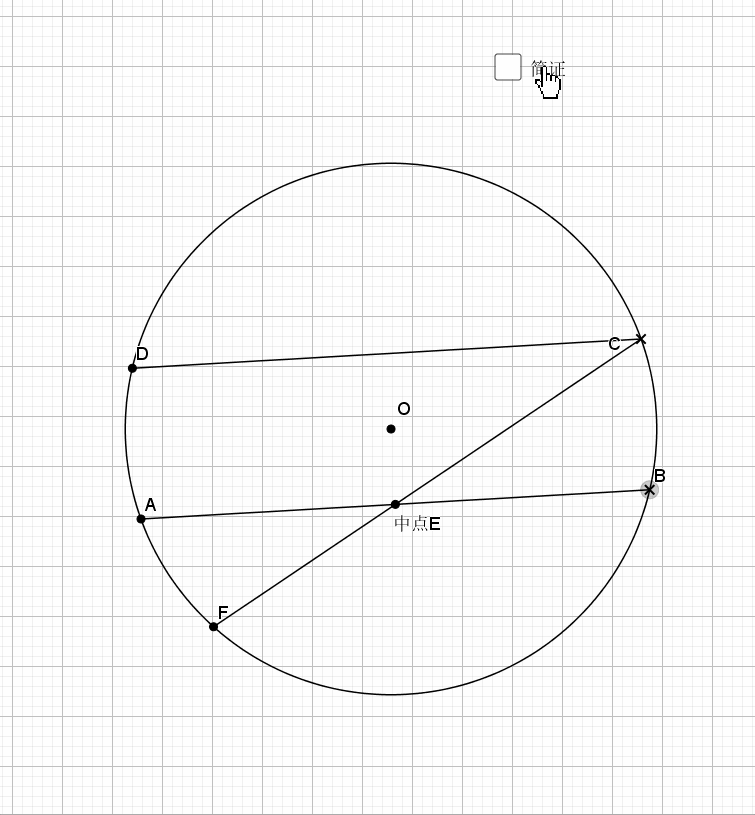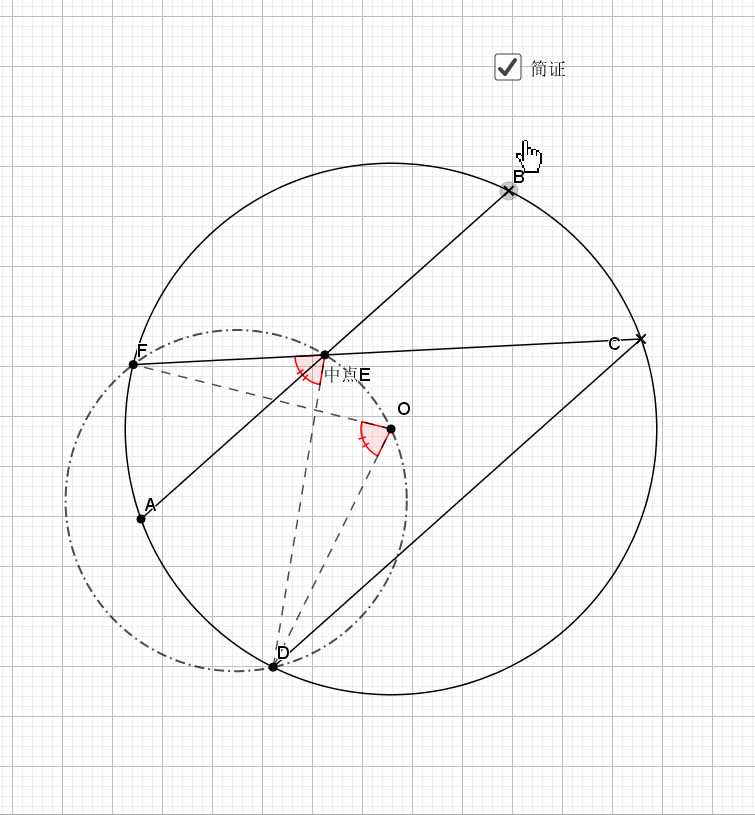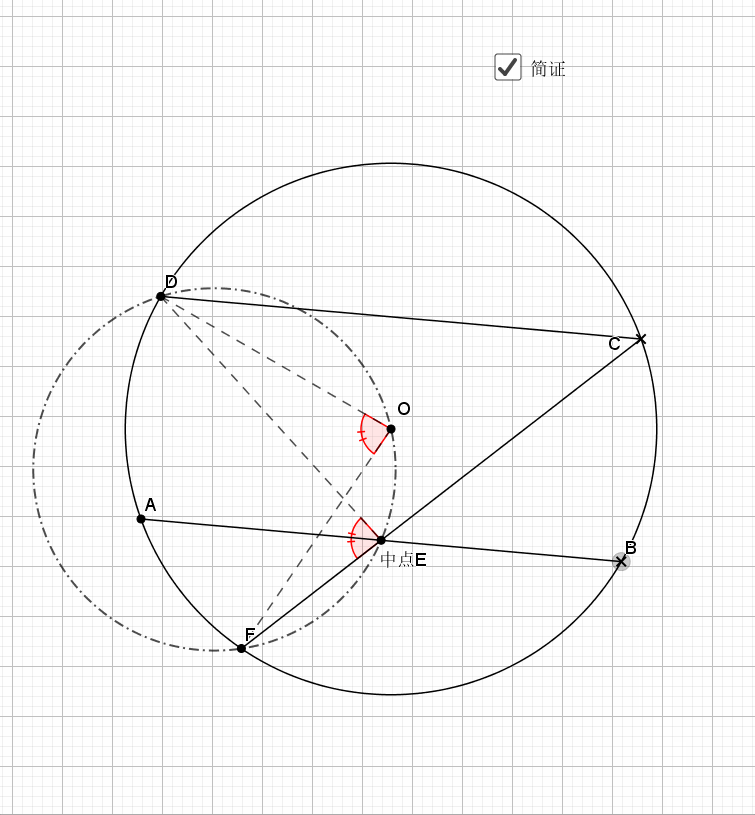
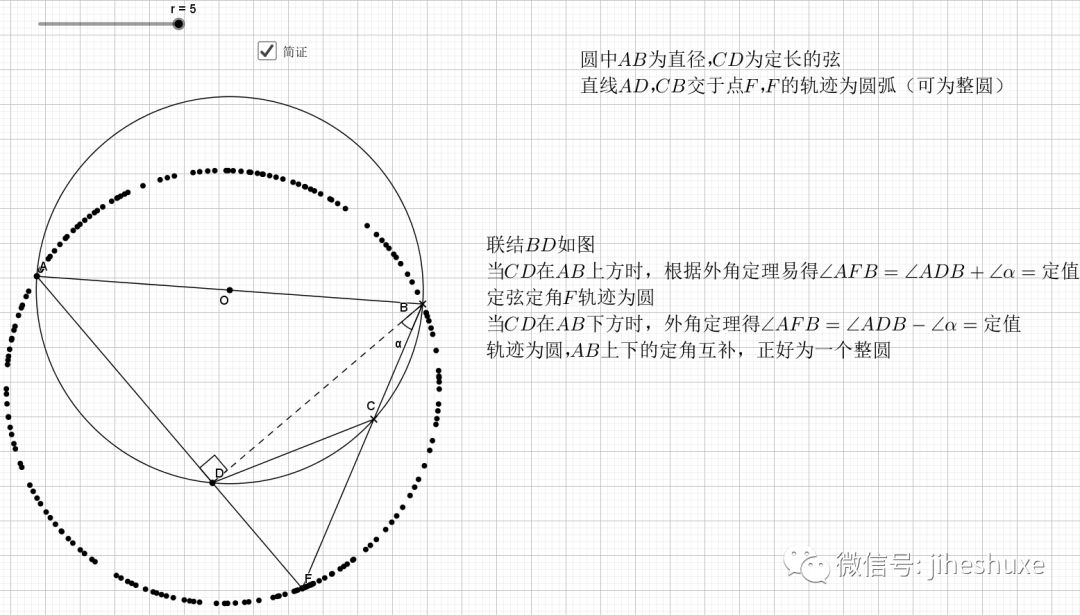
主要用到外角定理 ,圆心角圆周角关系等角度的知识,证明共圆用的是等弦对等角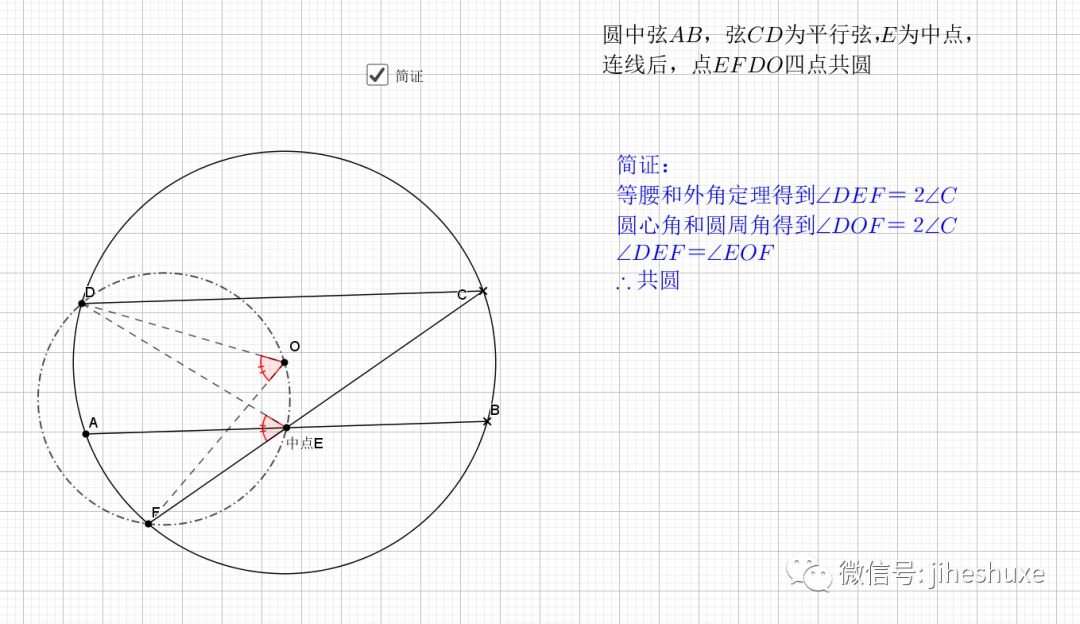
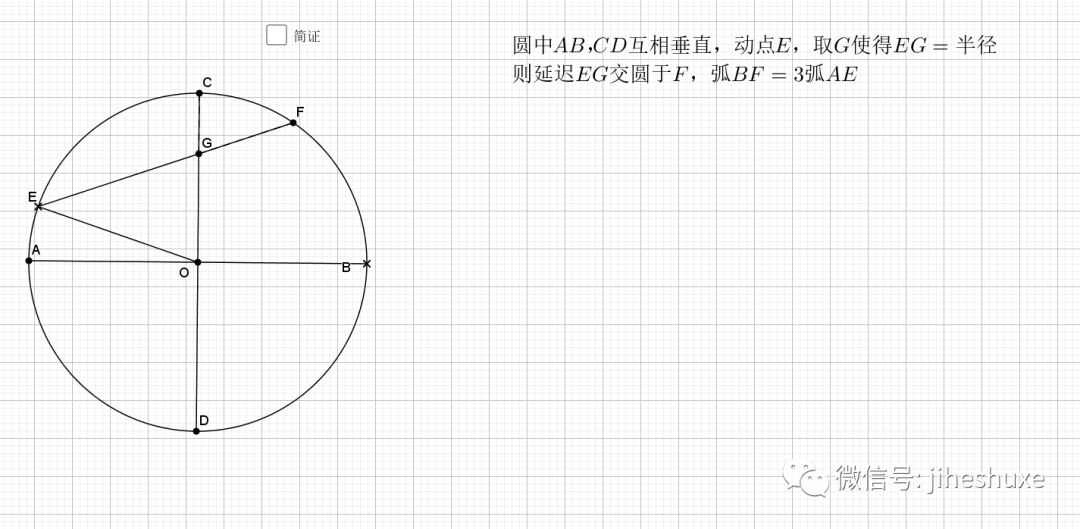
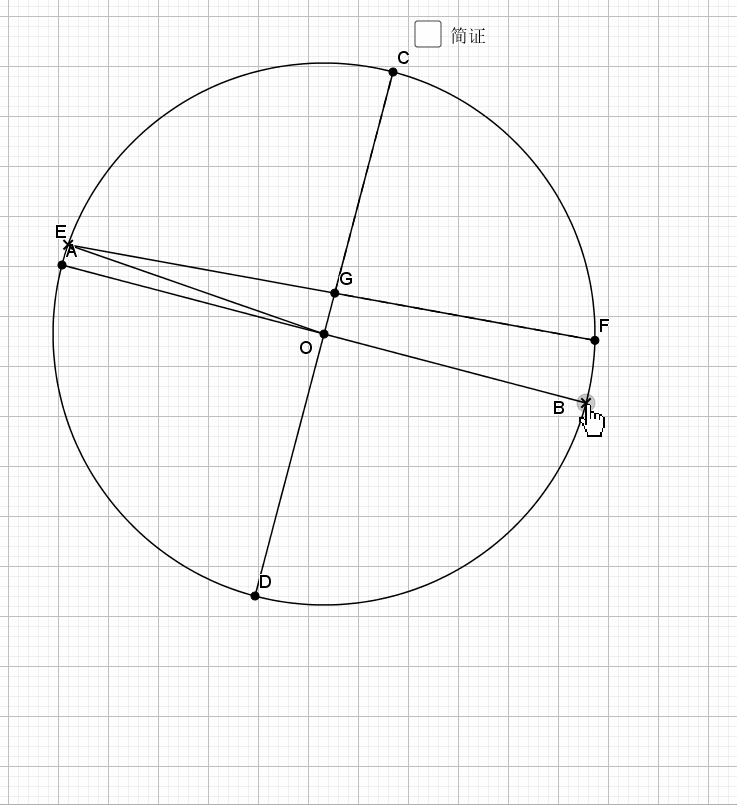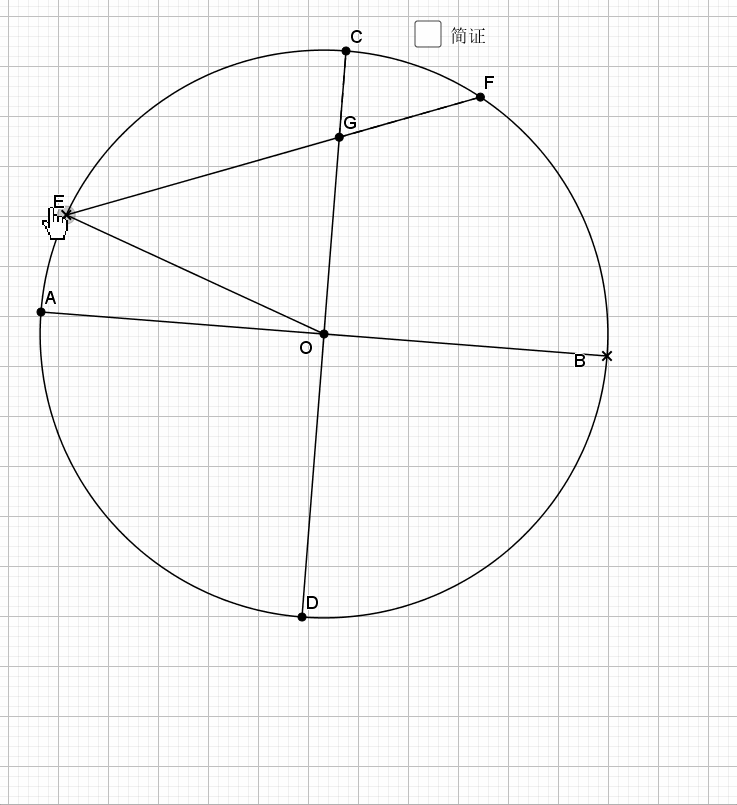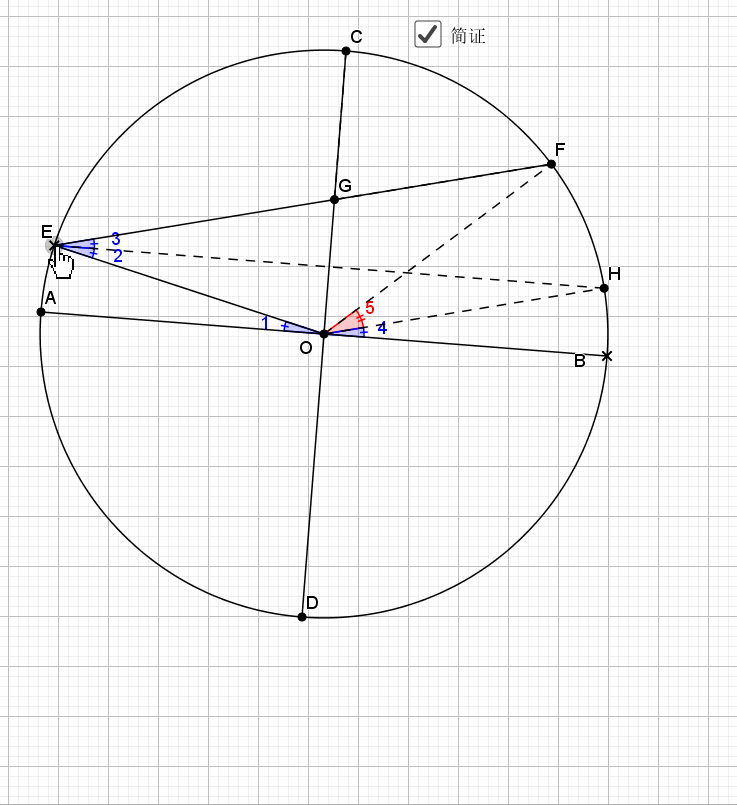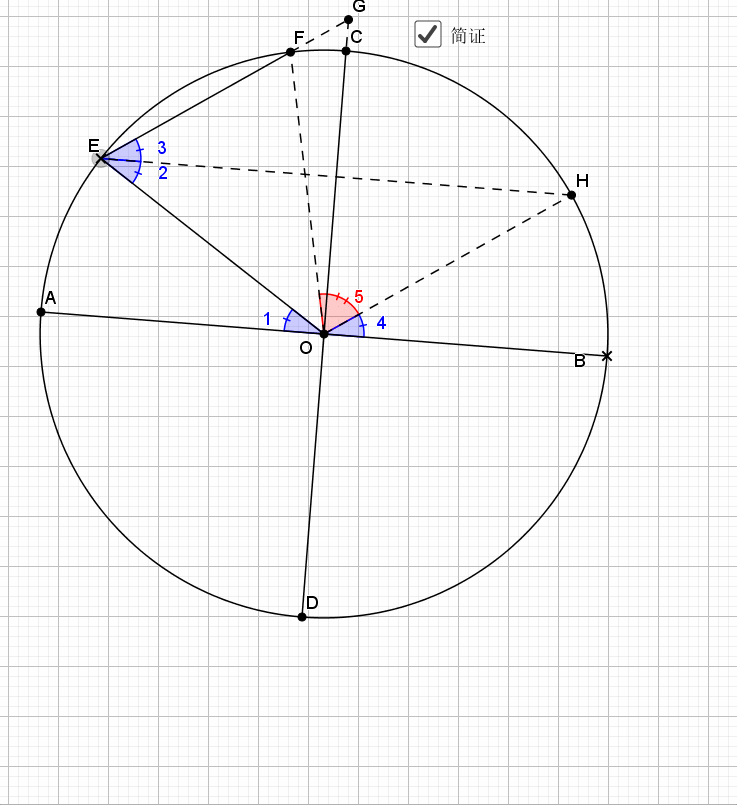
关键就是倒角,圆中的技术乐趣,尽在倒角上,借机回忆下和角有关的条件,有平行,等腰(还有圆中半径围成等腰),外角定理,内角和定理,圆中的圆周角,圆心角,圆内接四边形的内对角,外角等等。
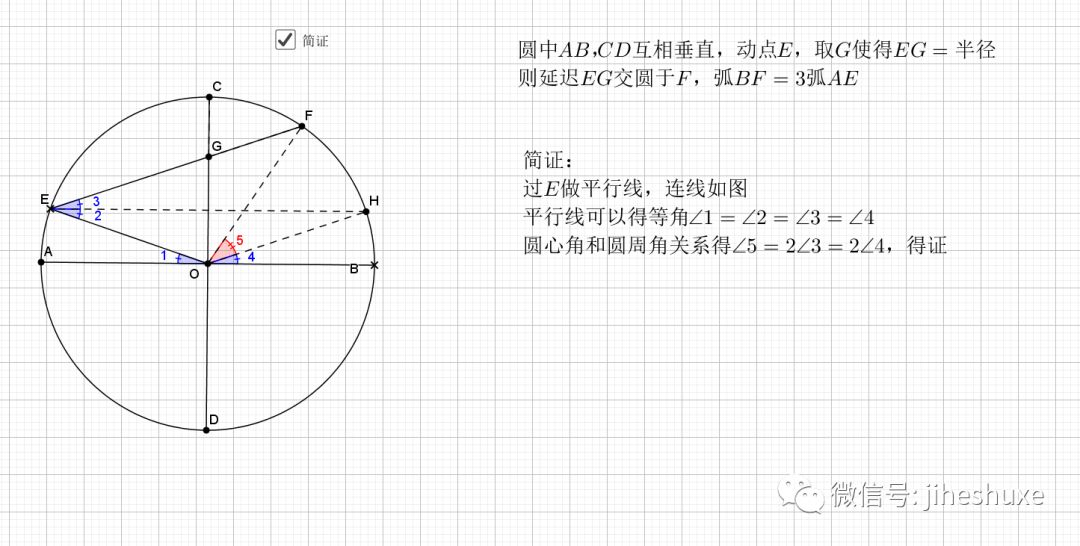
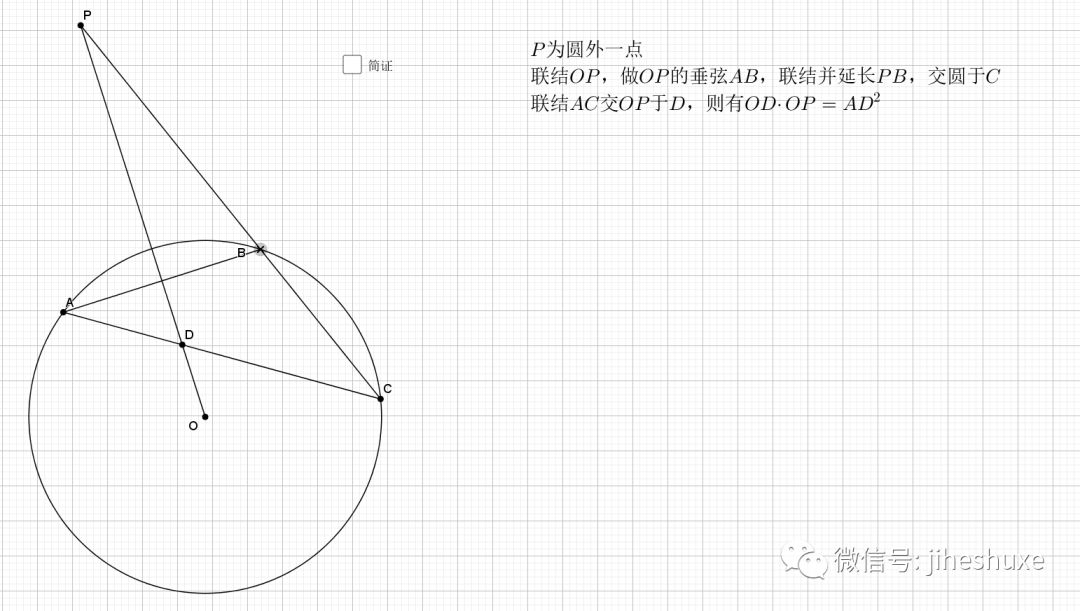
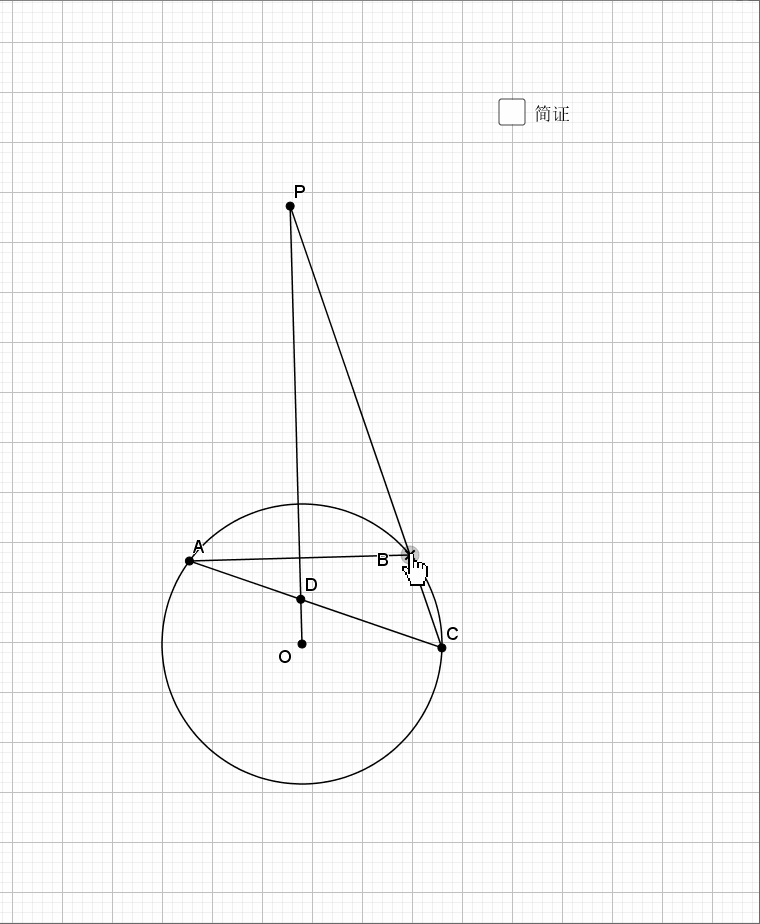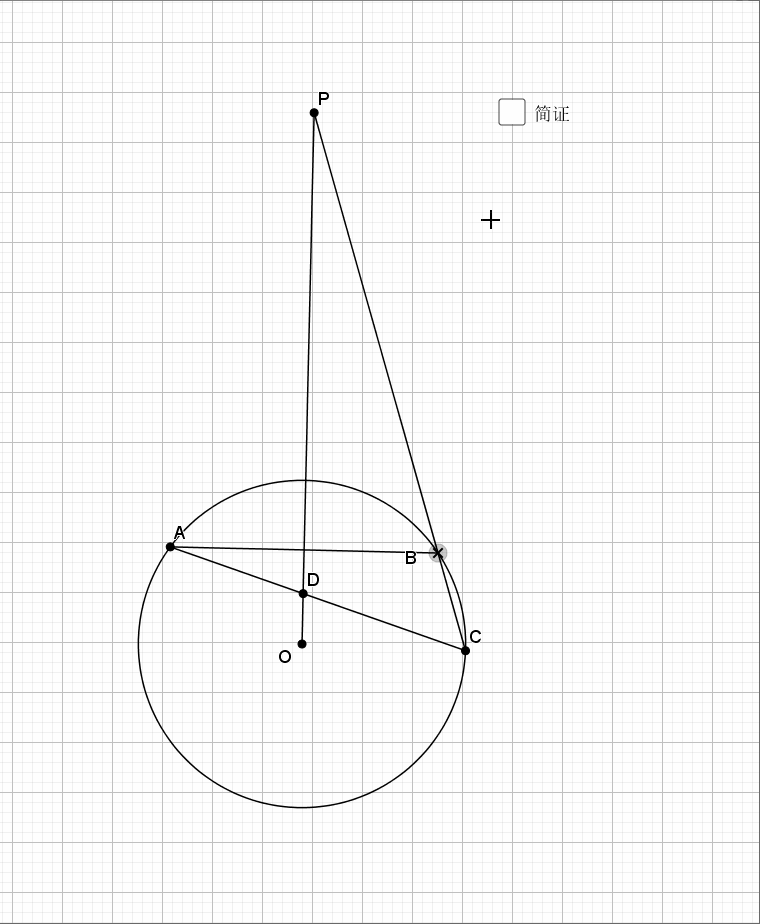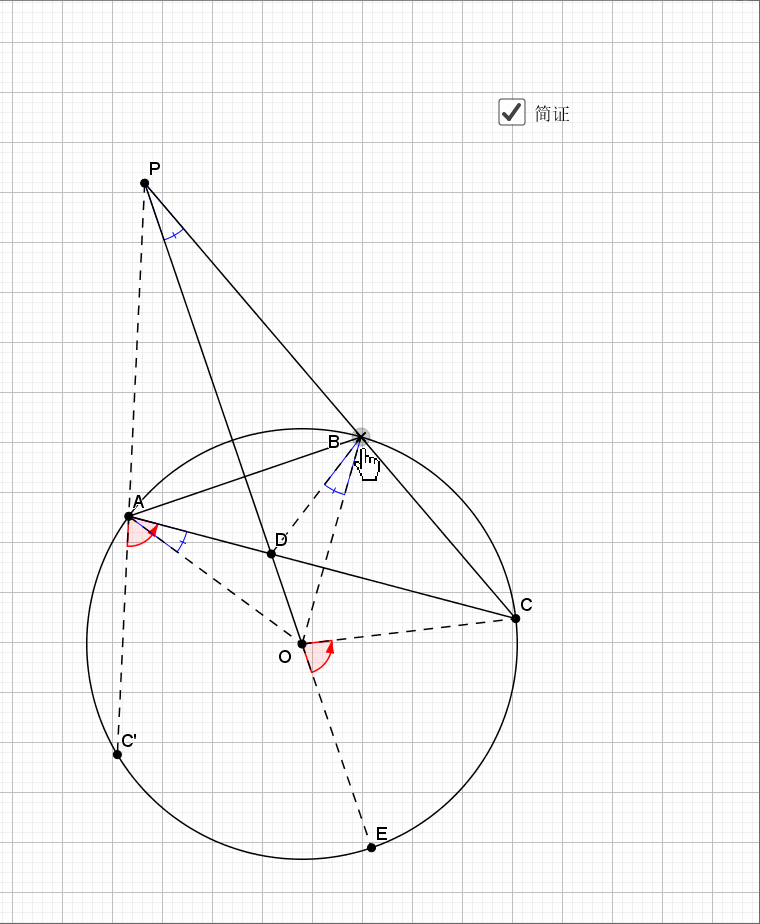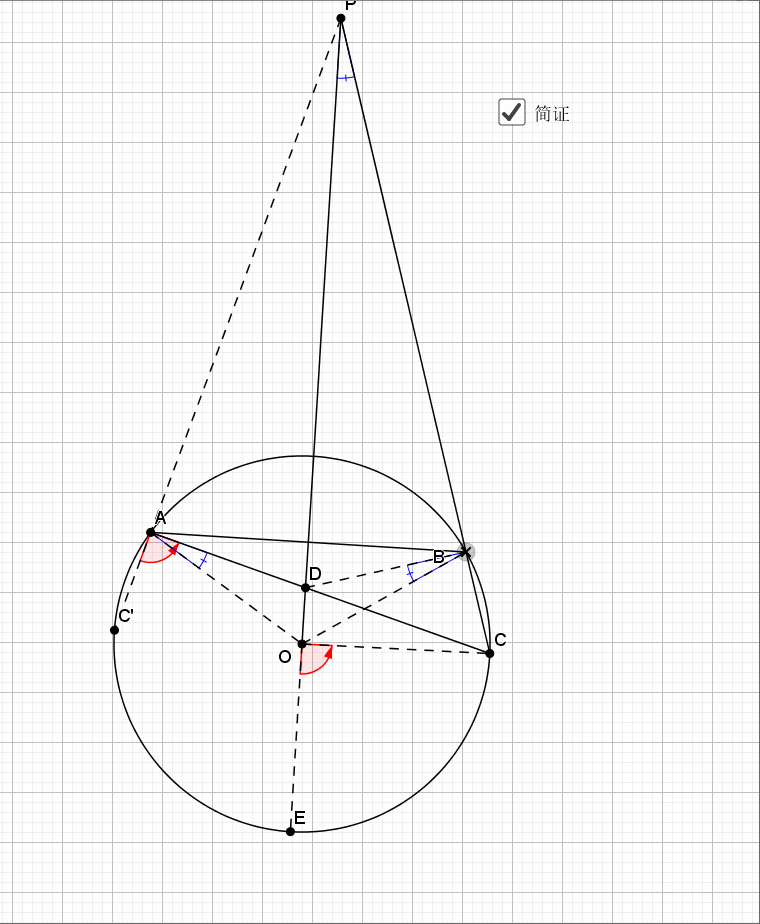
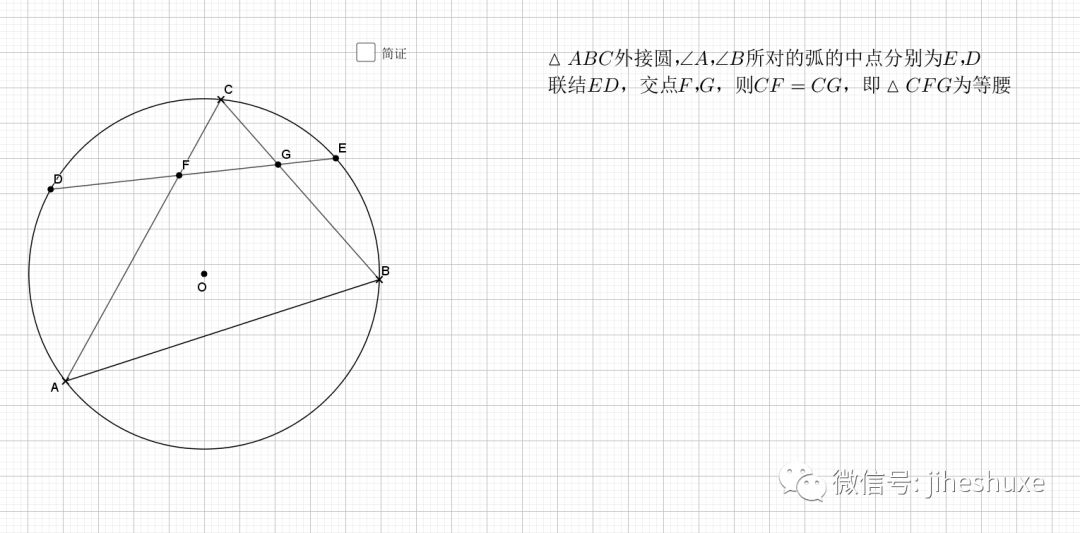
利用对称性,圆周角和圆心角,等弧对等角(弧的倍数等于圆周(心)角的倍数),最后结论是经典的字母型的线段关系。推出字母相似即可。
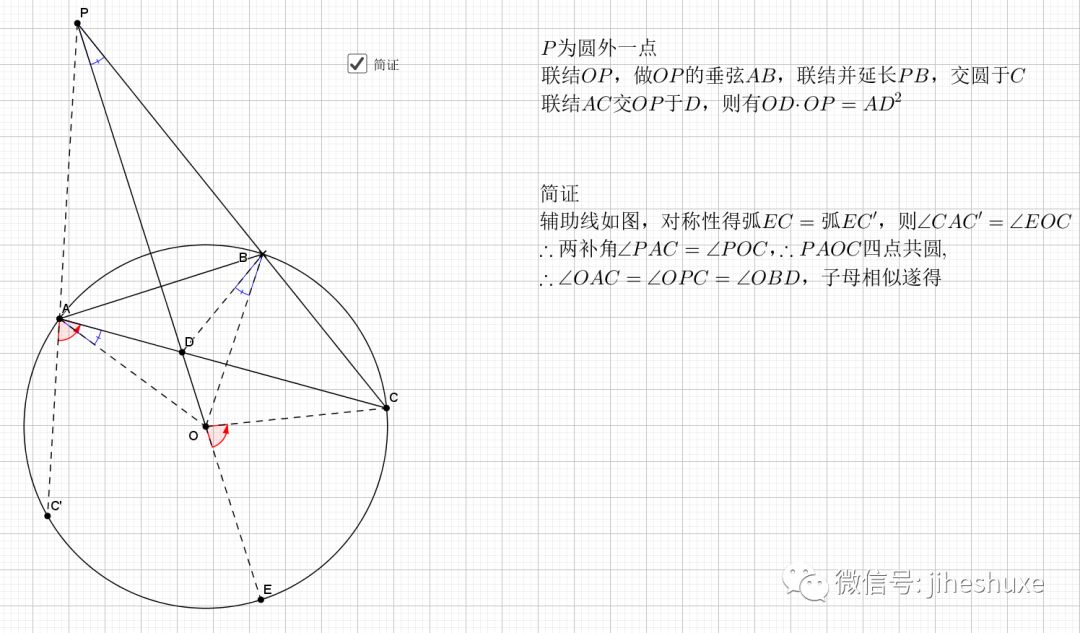
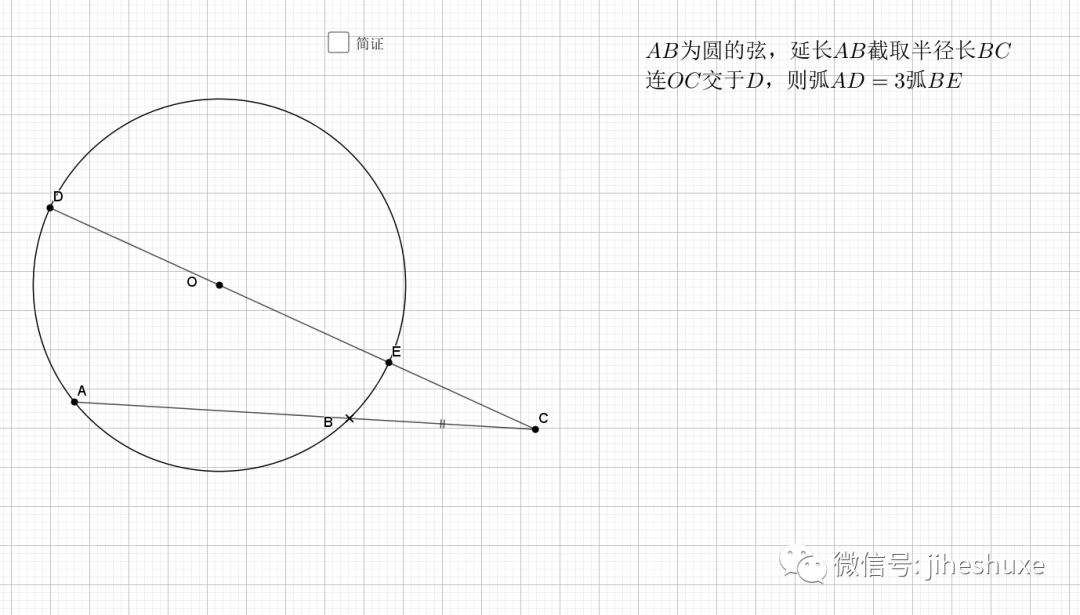
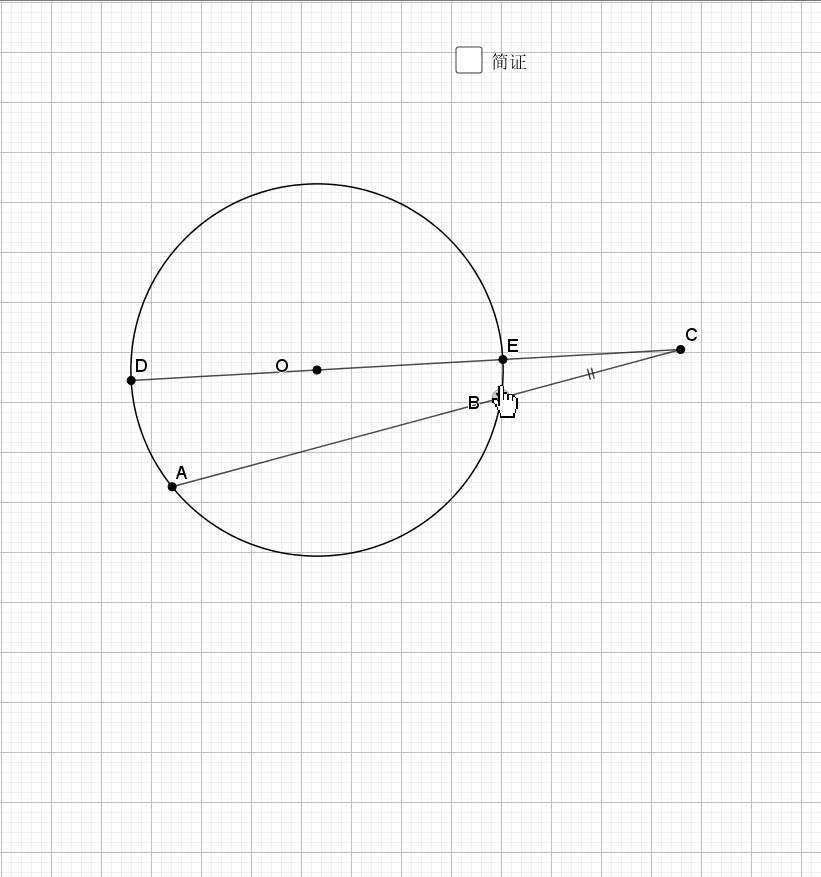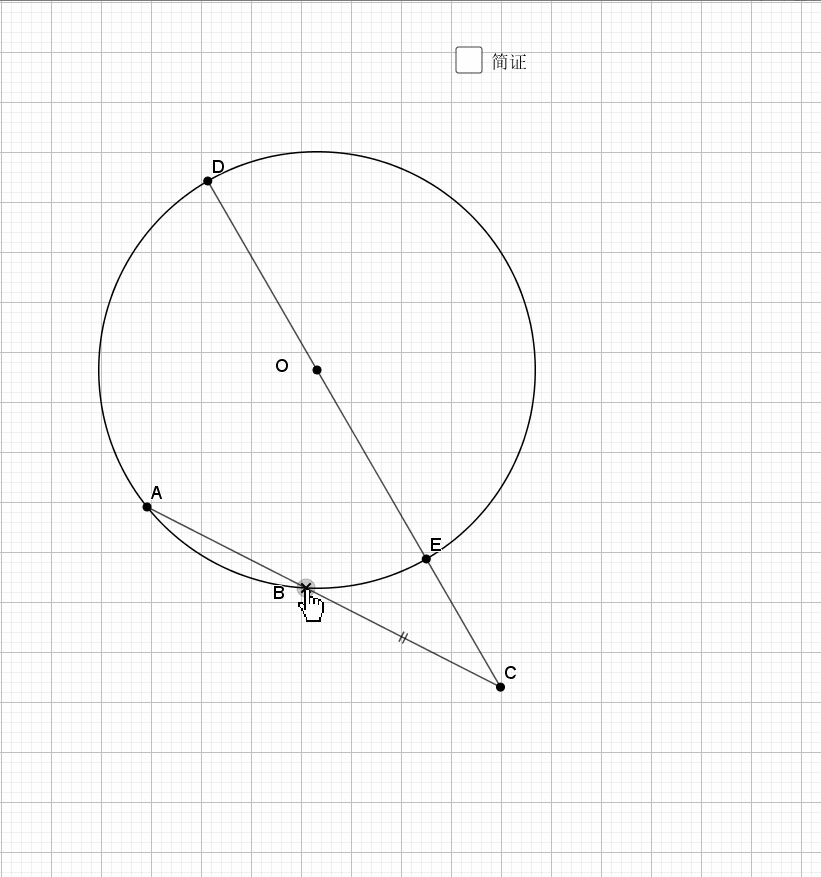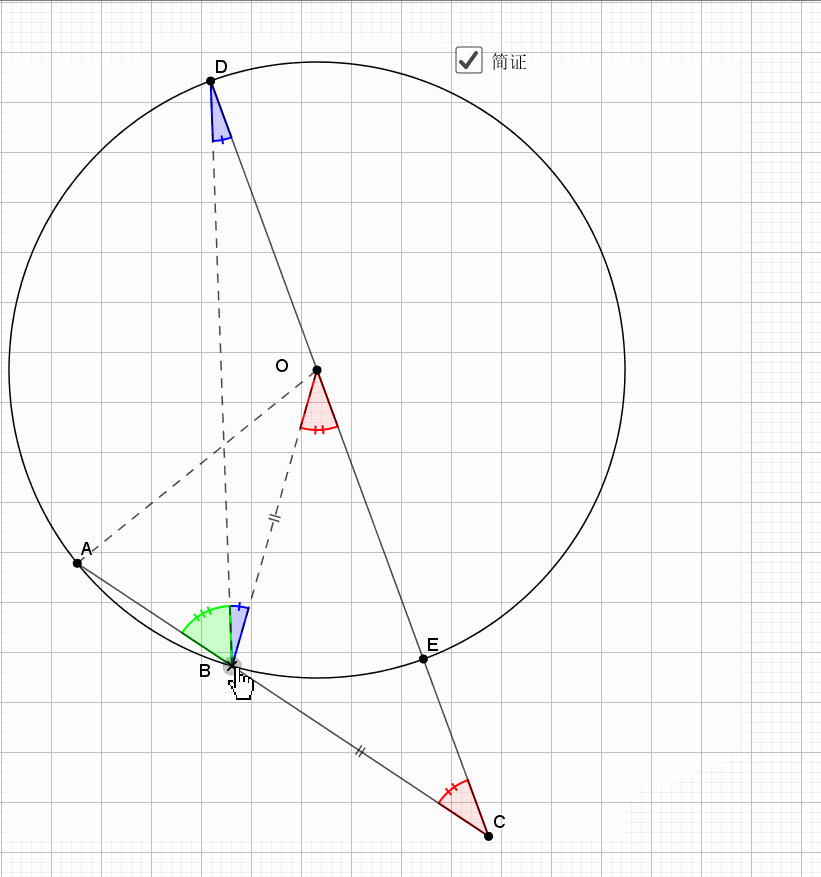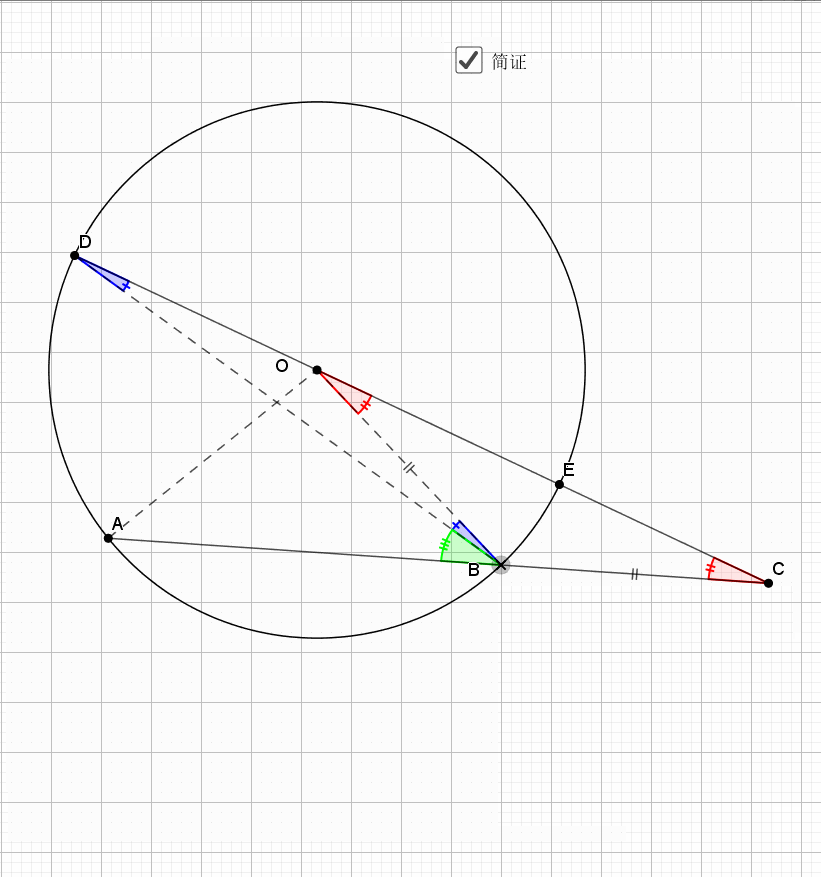
无疑还是倒角
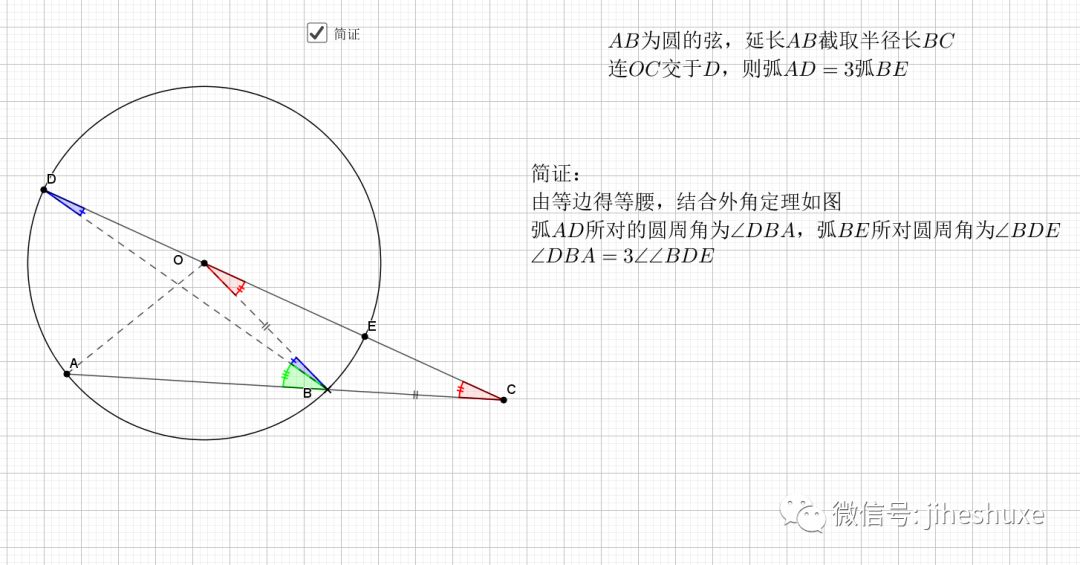
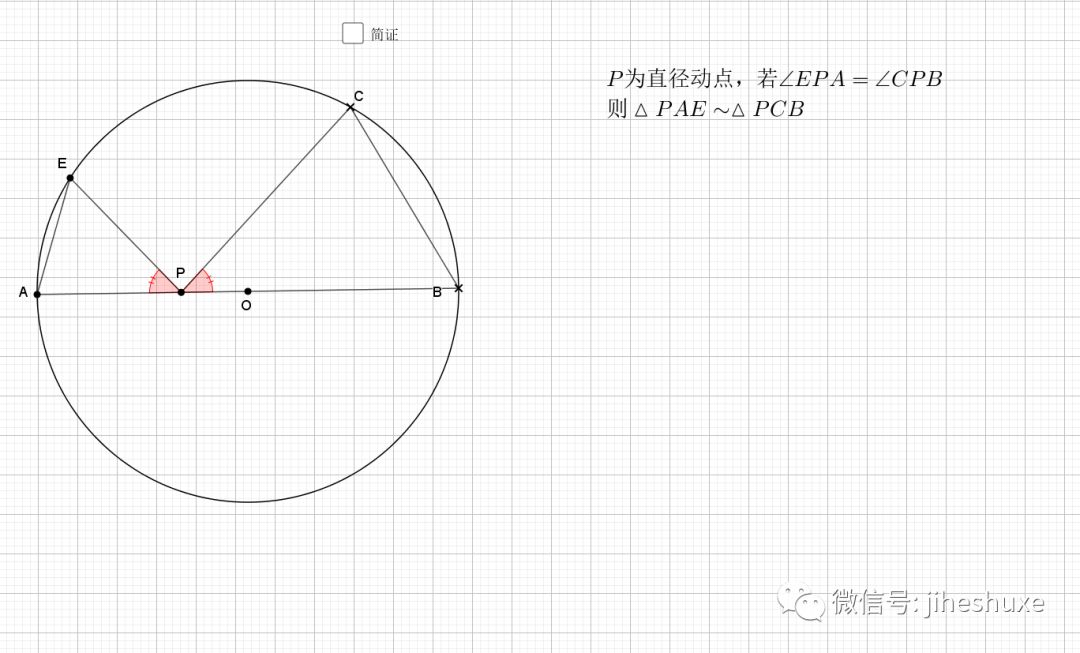
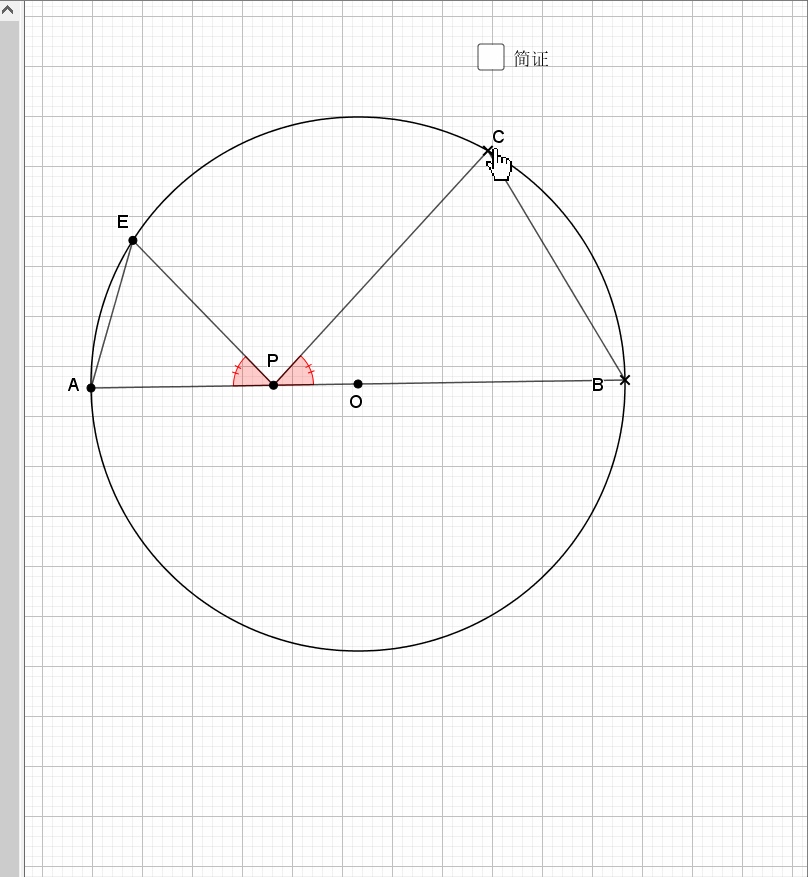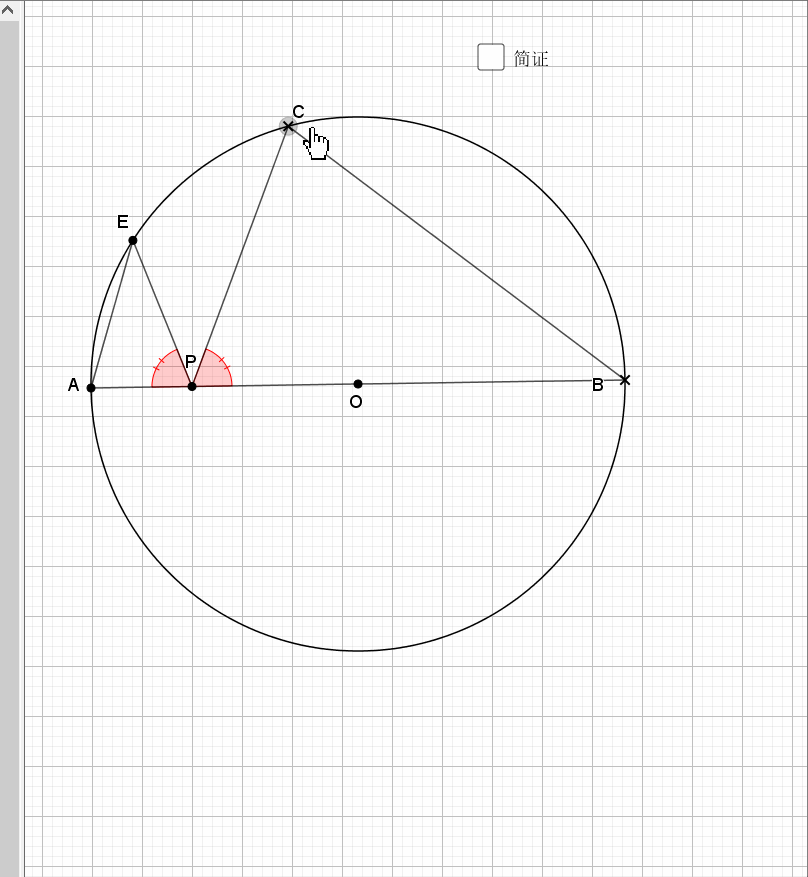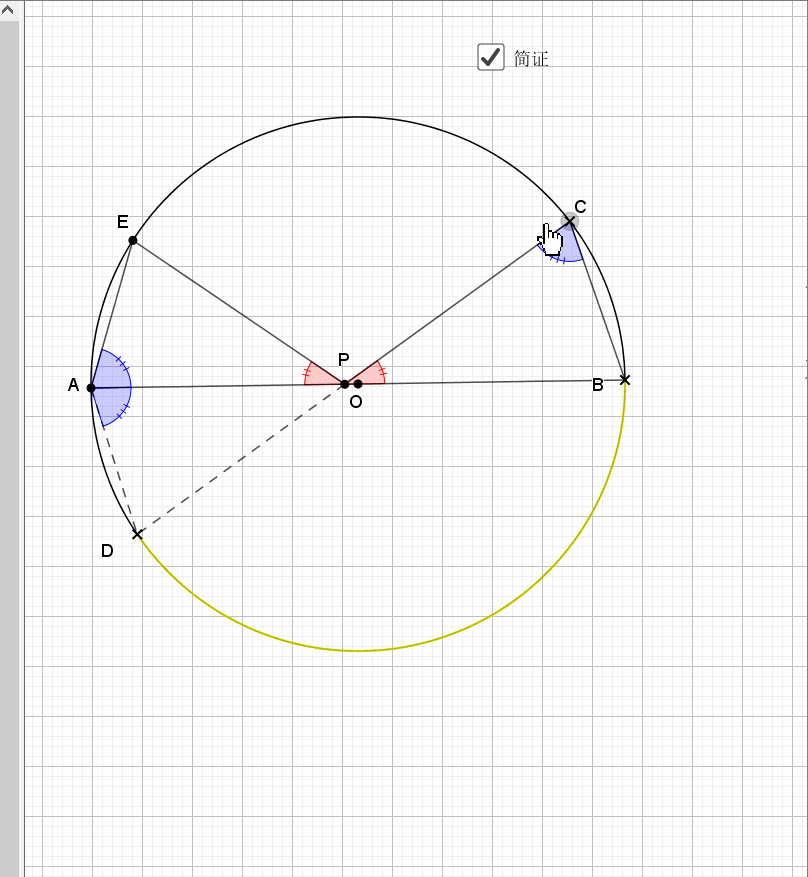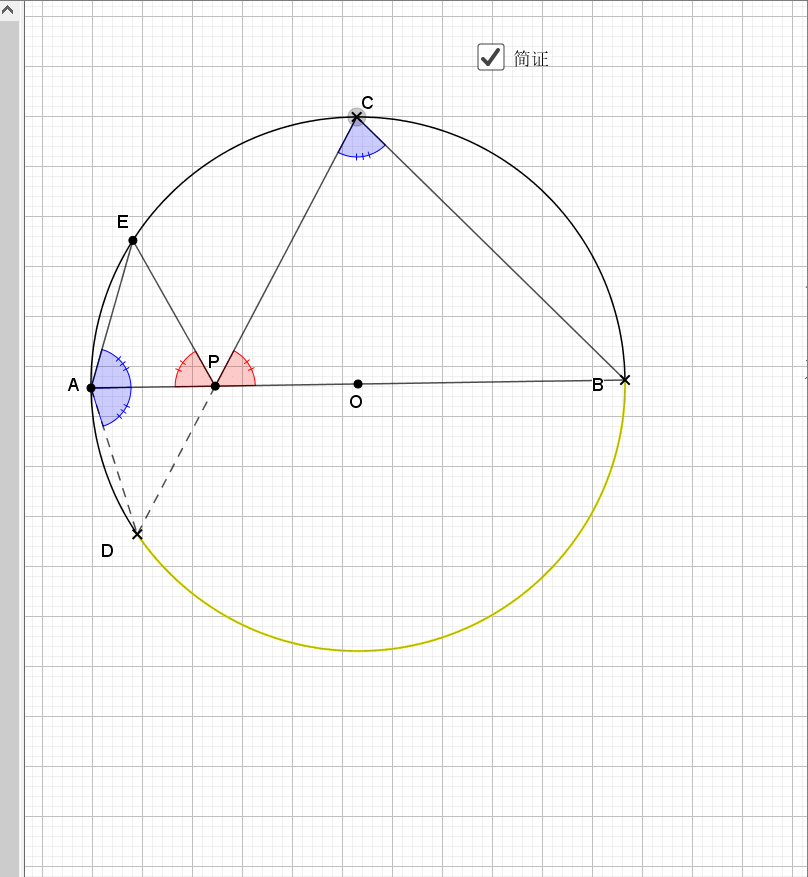
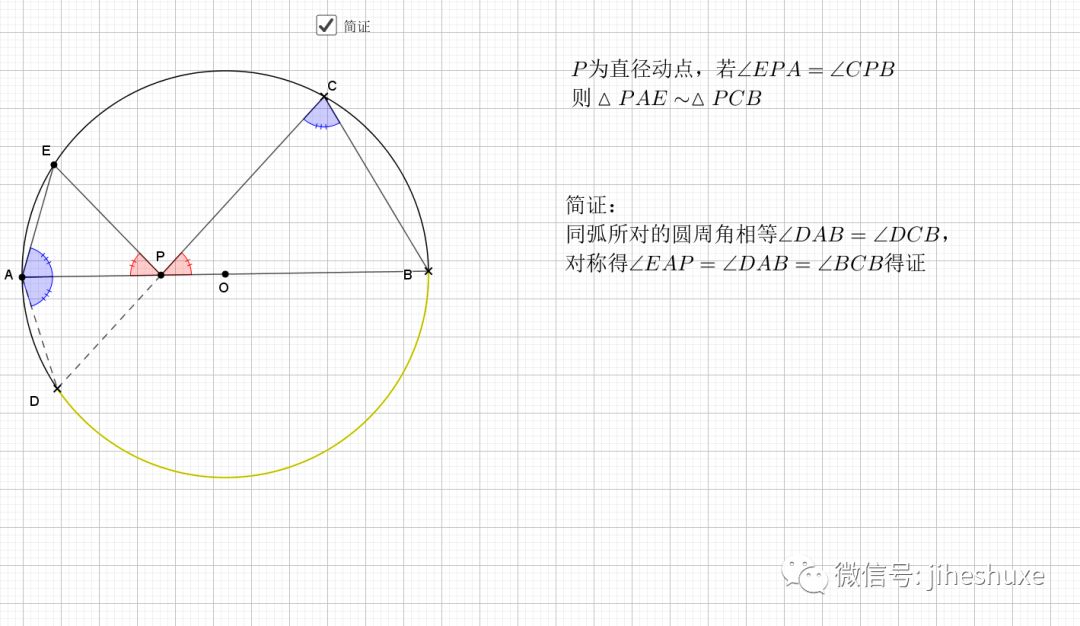
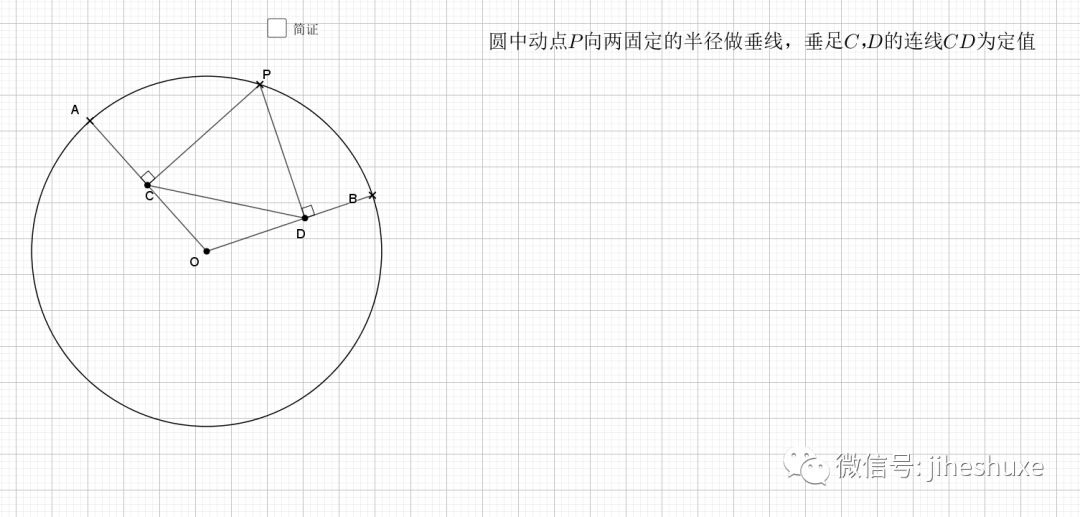
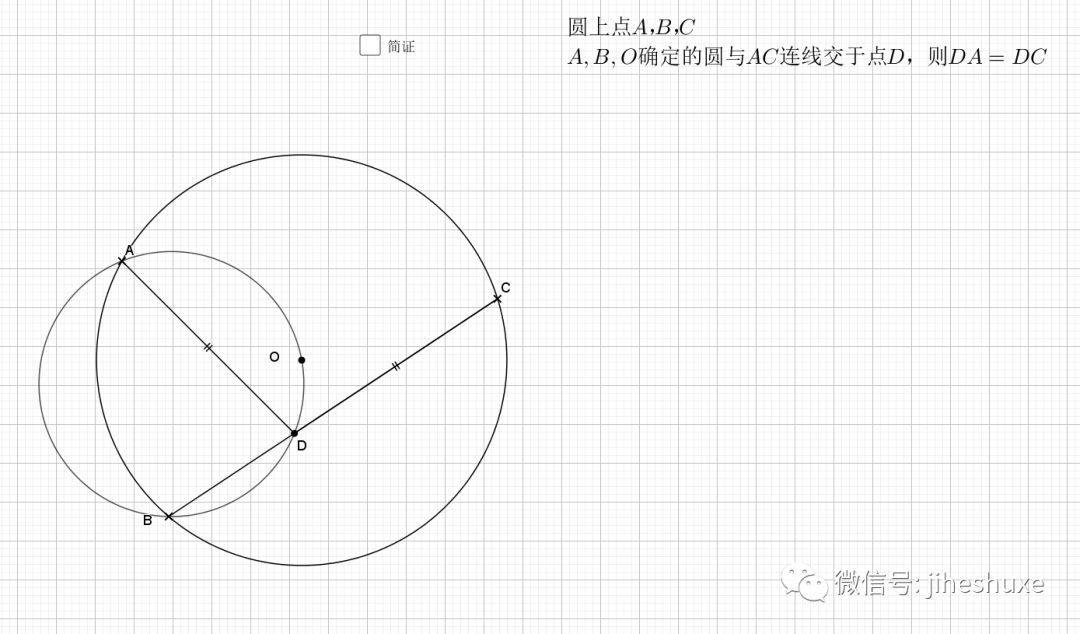
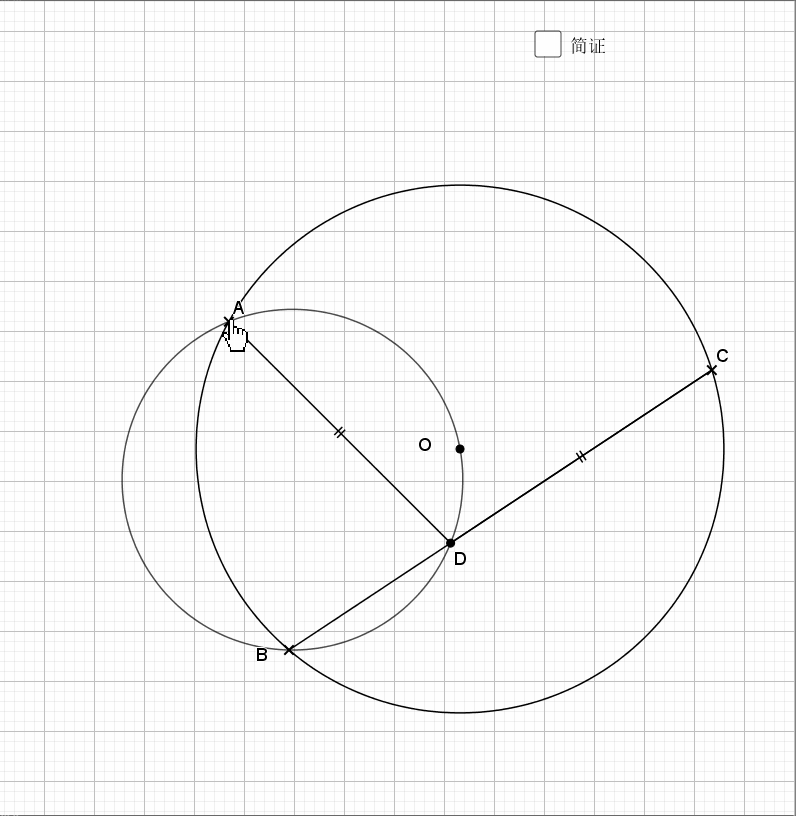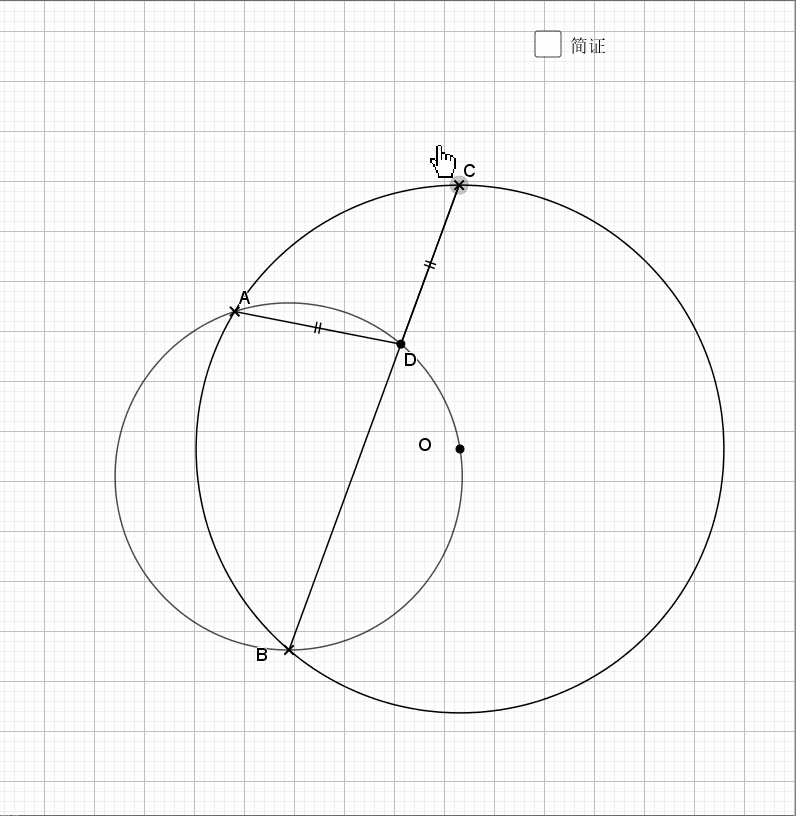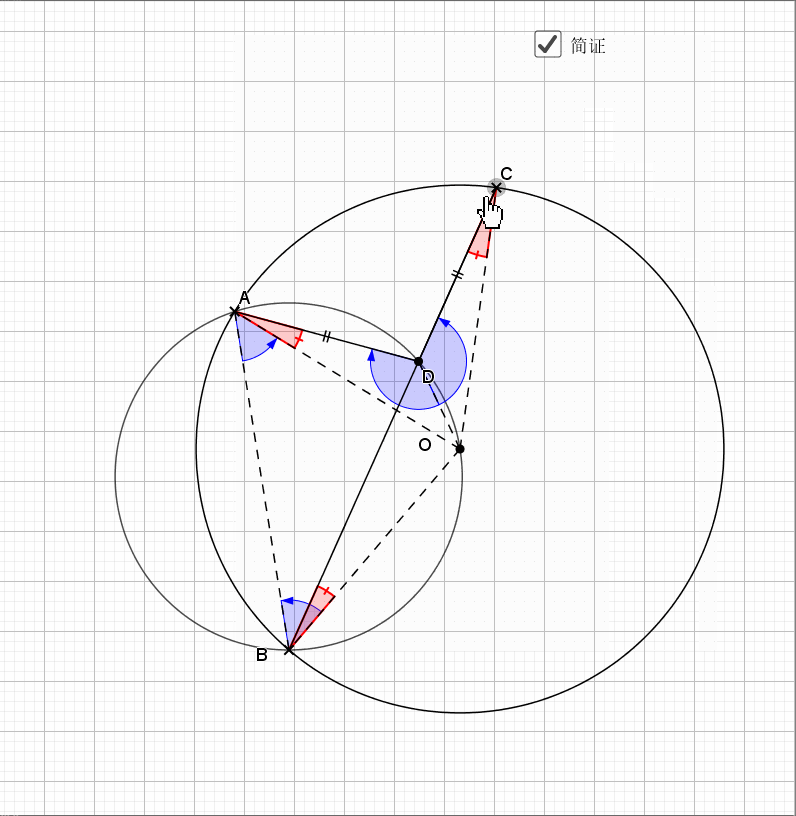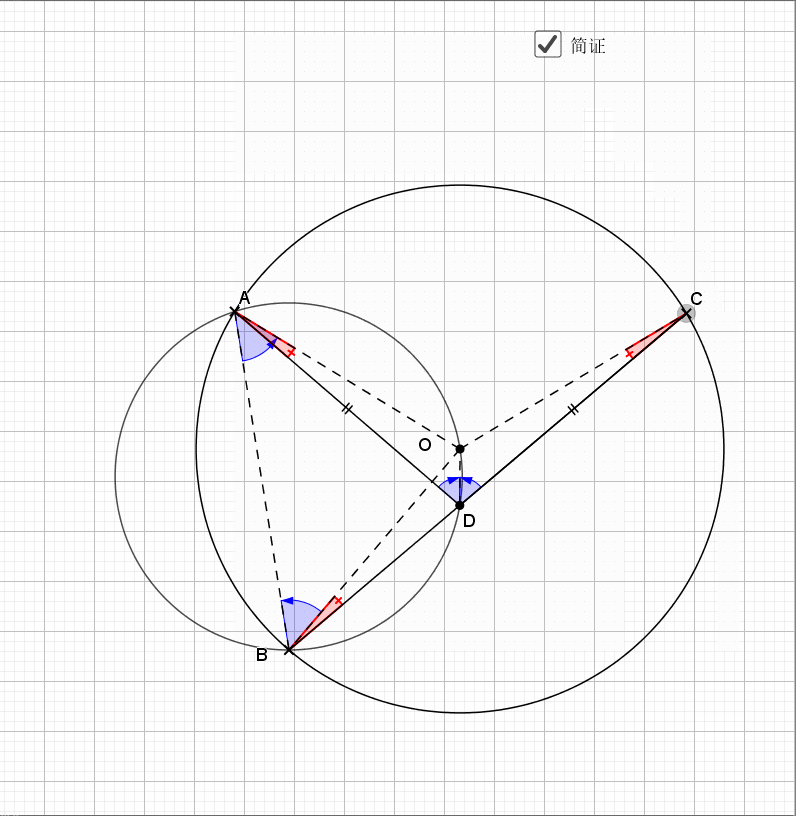
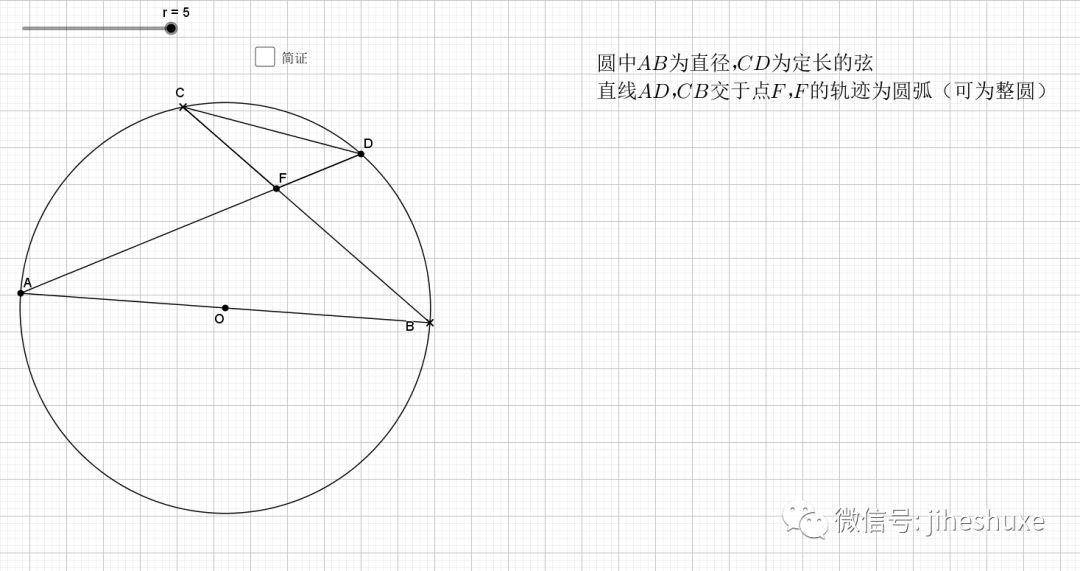
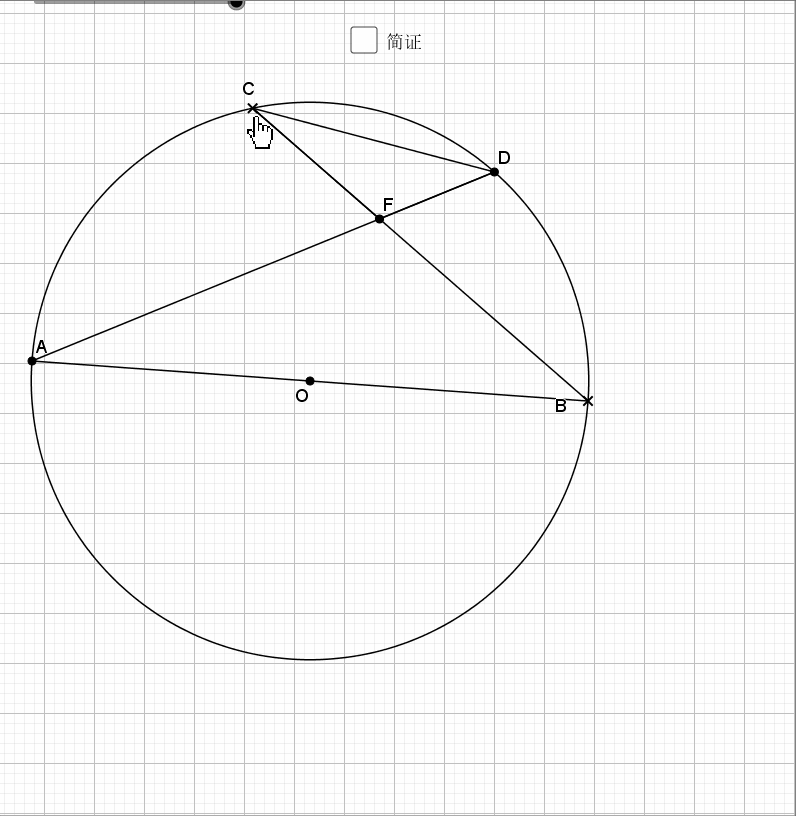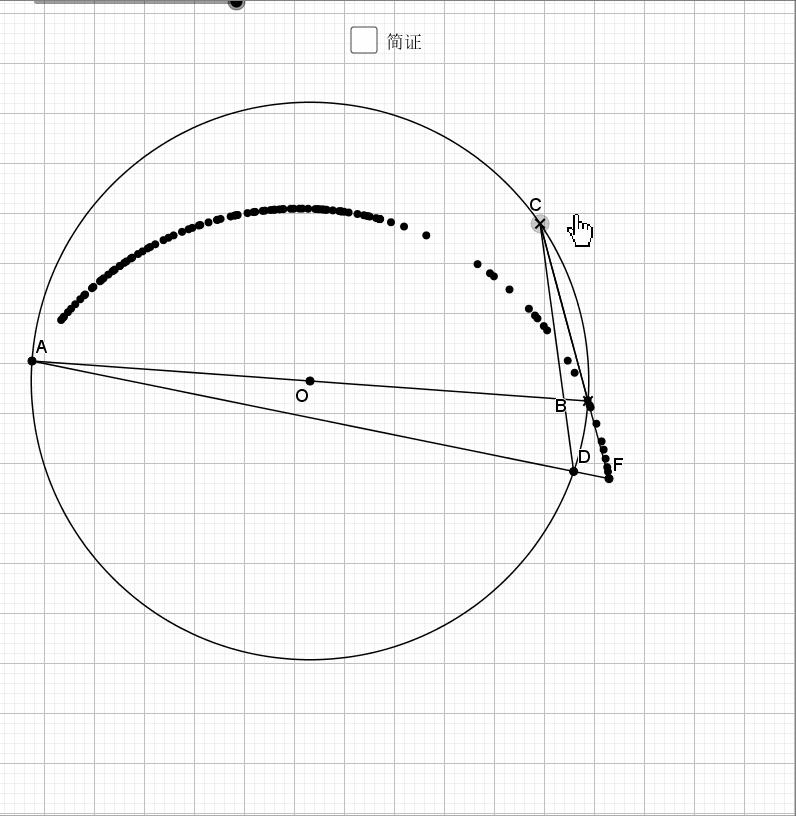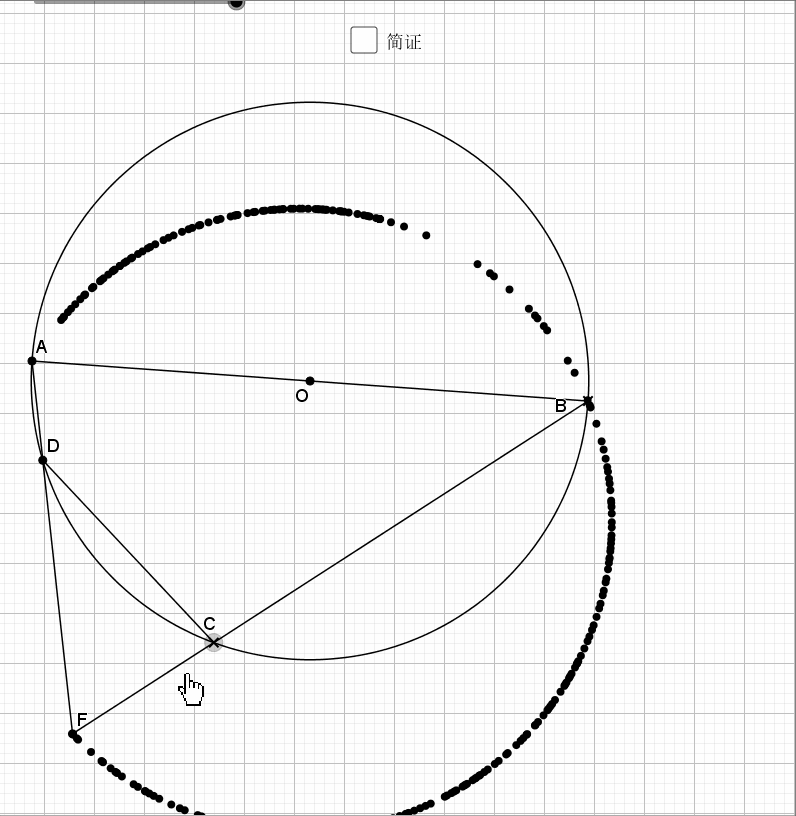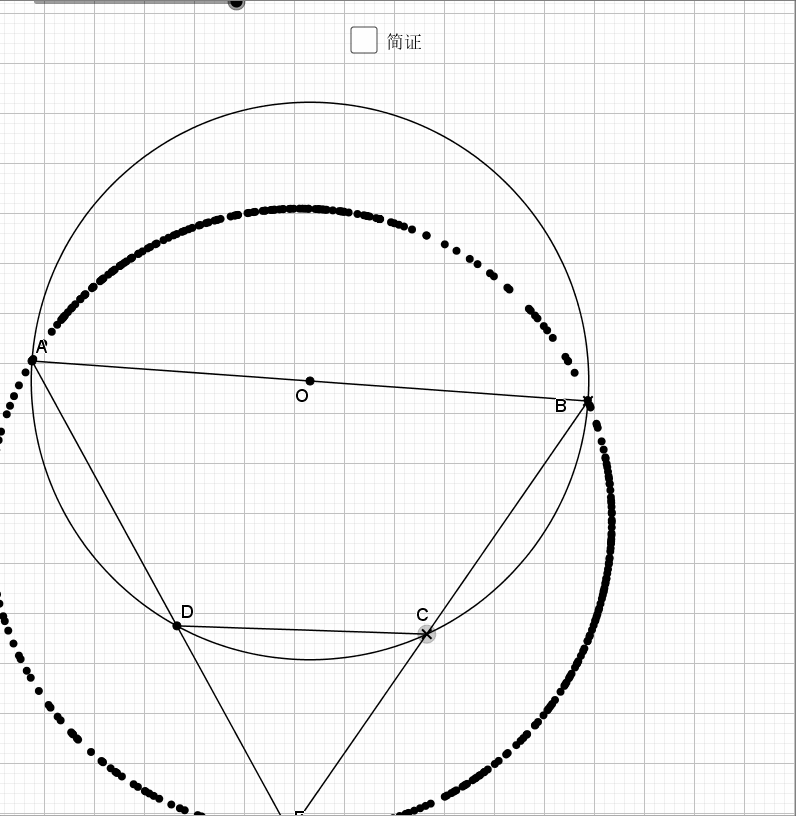
 相似还是由角来得到,圆中多的是和角相关的性质。
相似还是由角来得到,圆中多的是和角相关的性质。
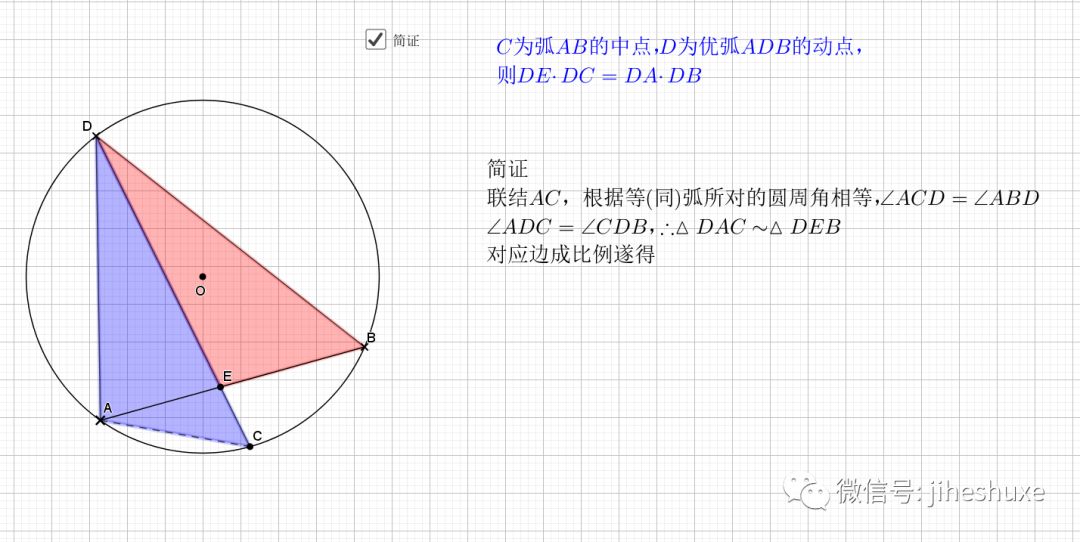
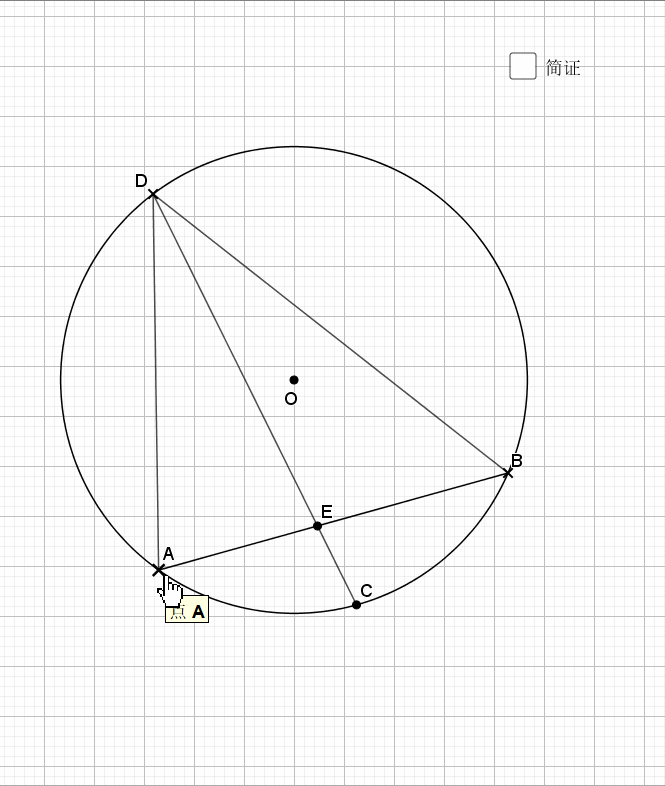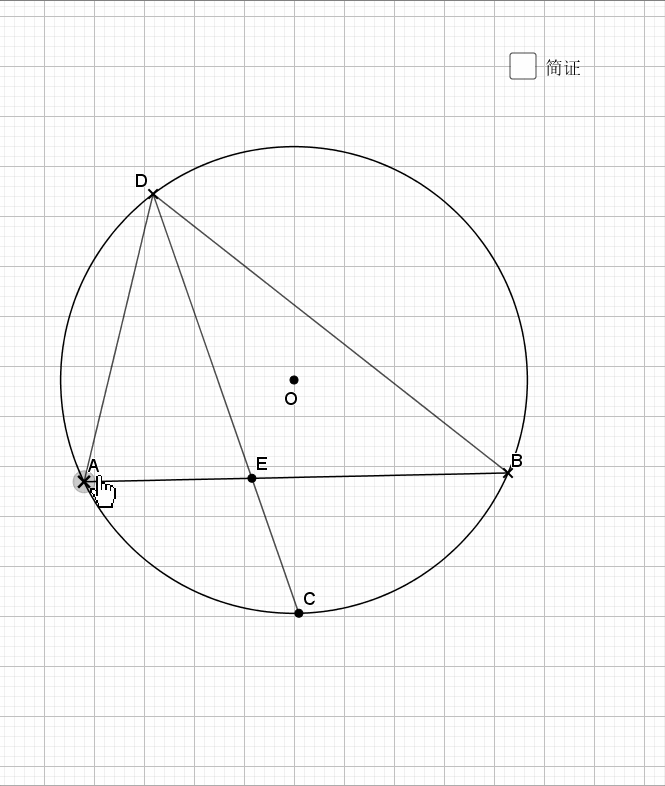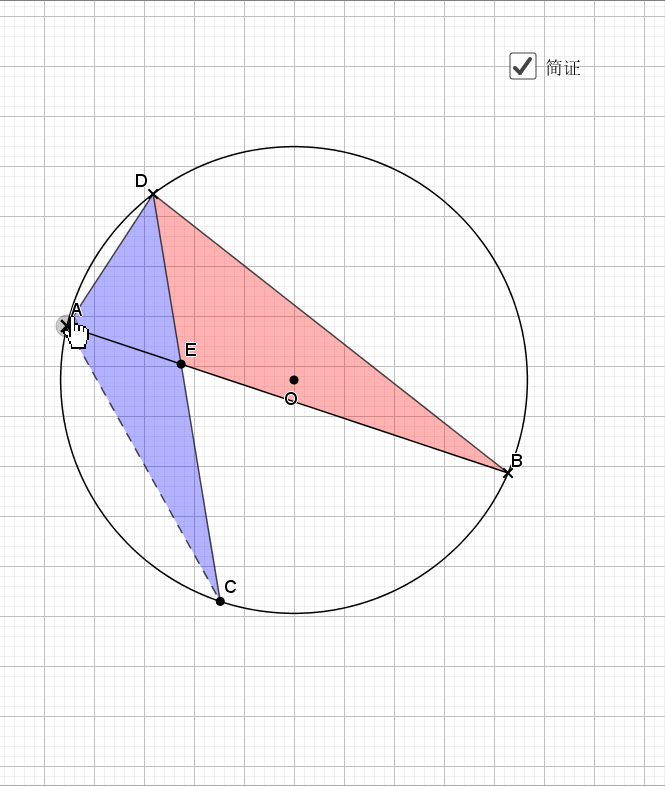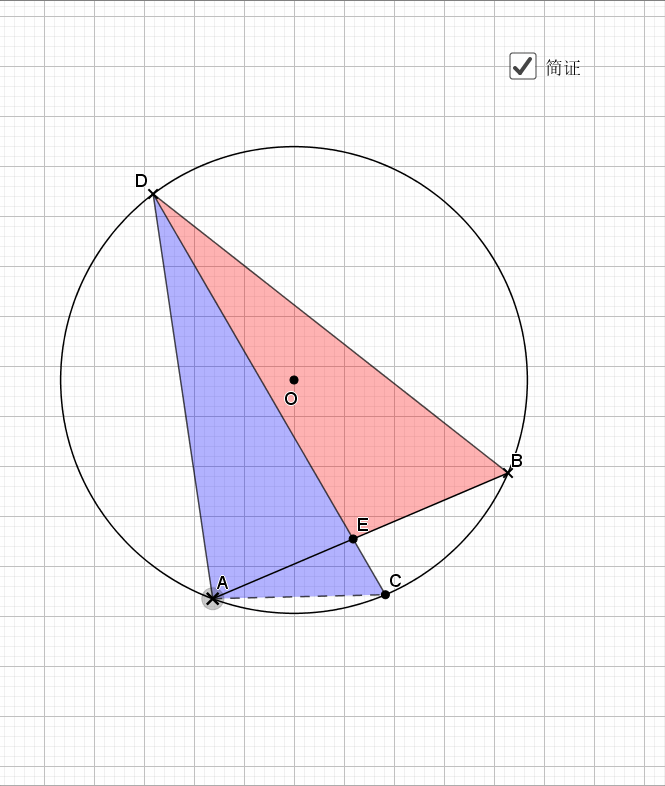
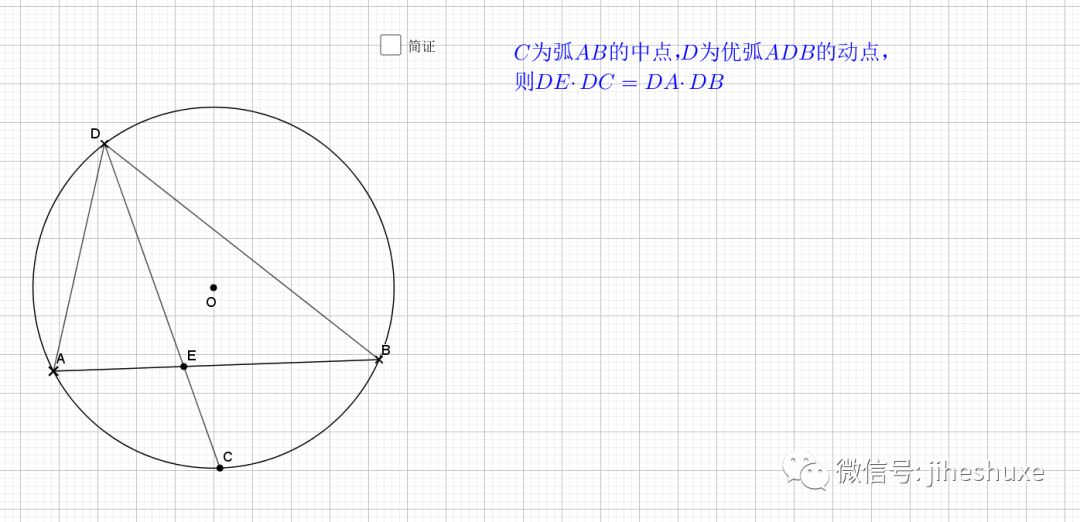
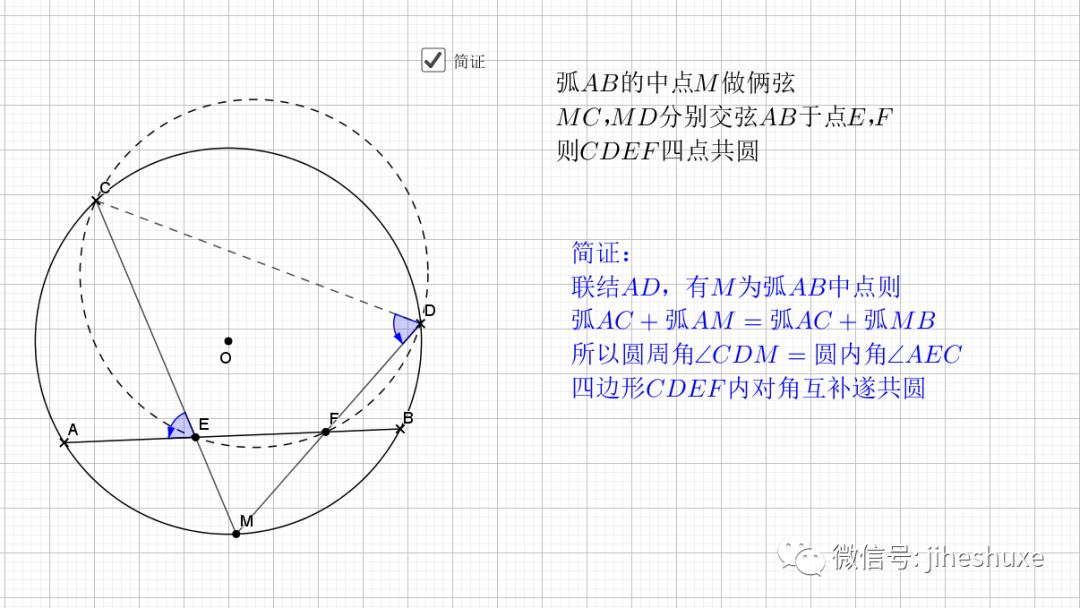
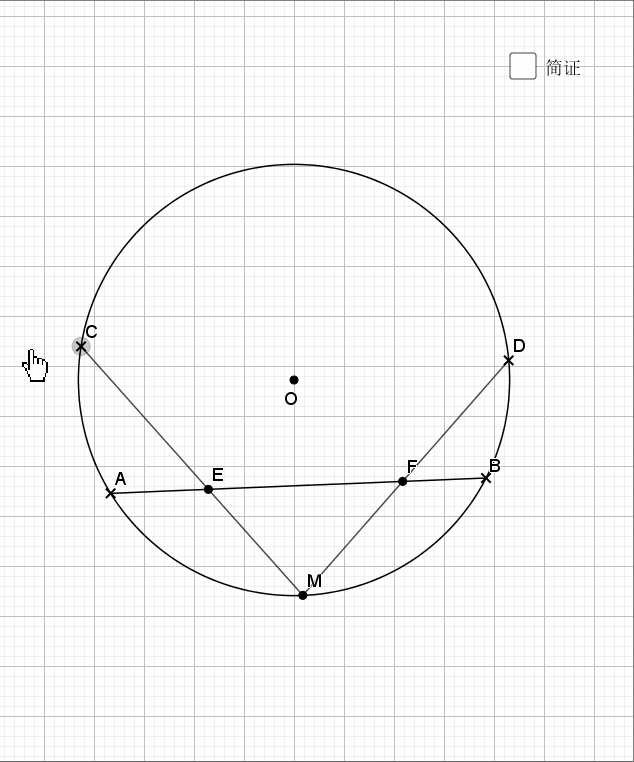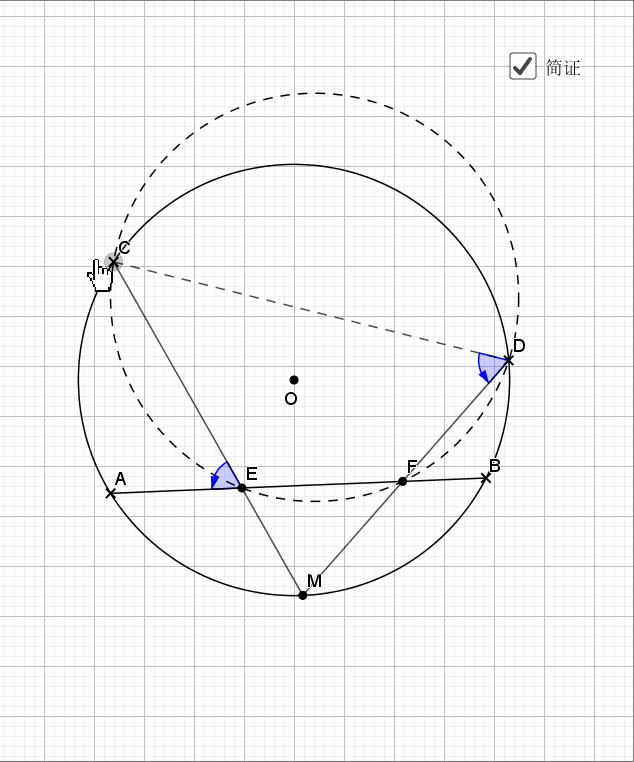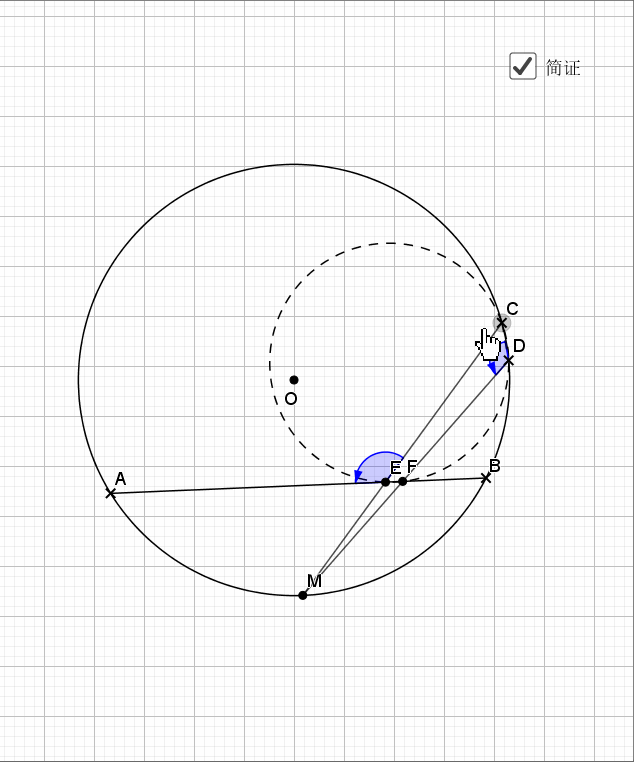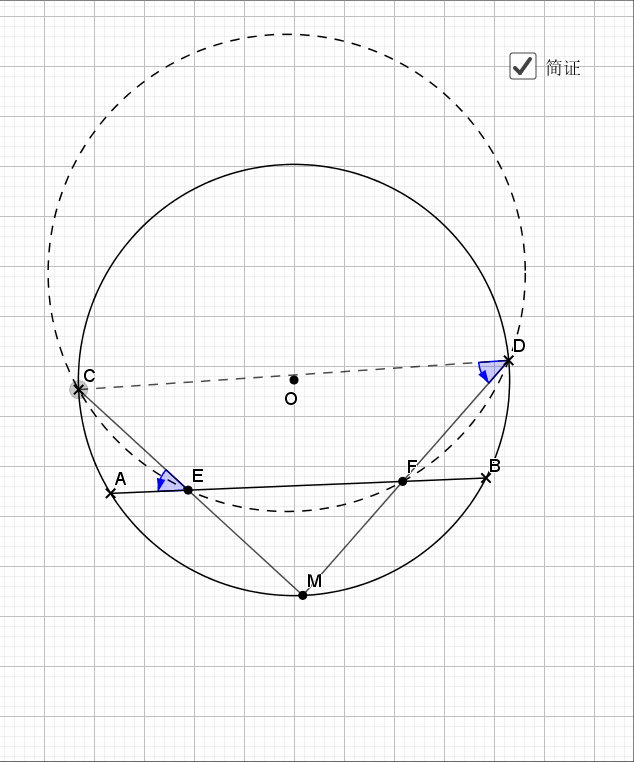
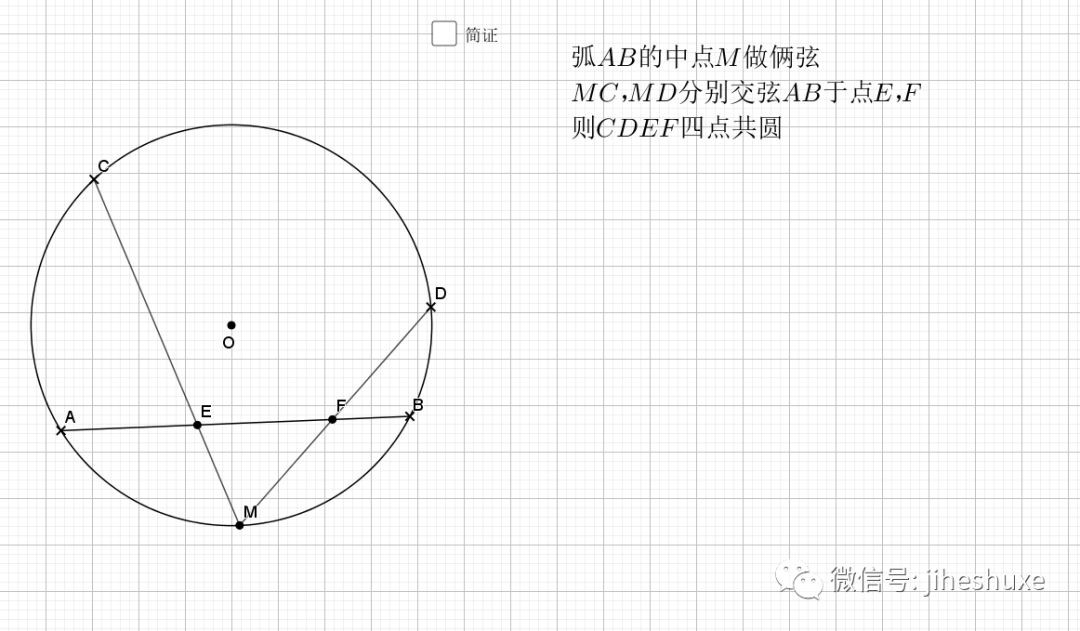 还是弧中点,其实象征的等角,由等角再到共圆。
还是弧中点,其实象征的等角,由等角再到共圆。
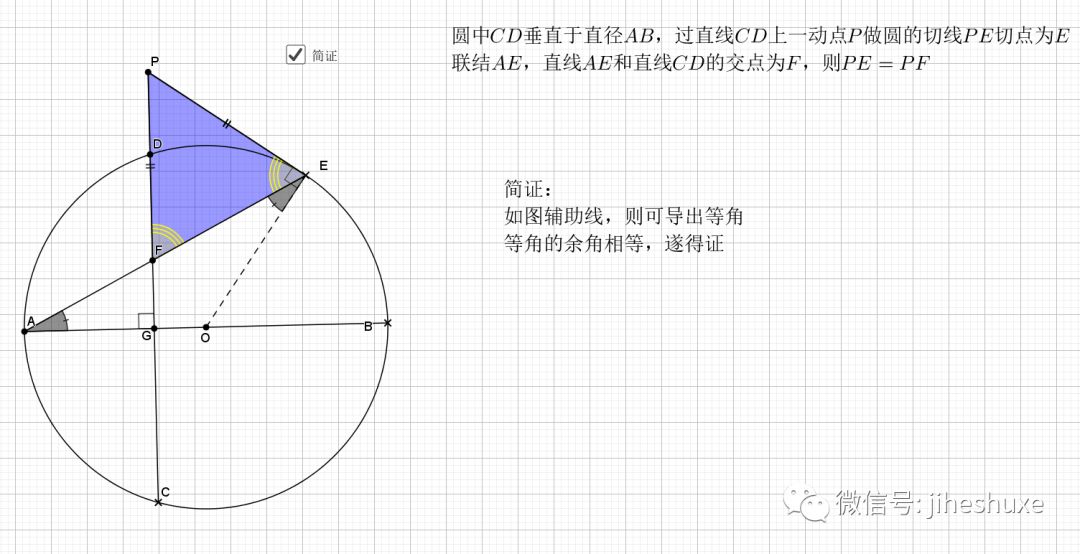
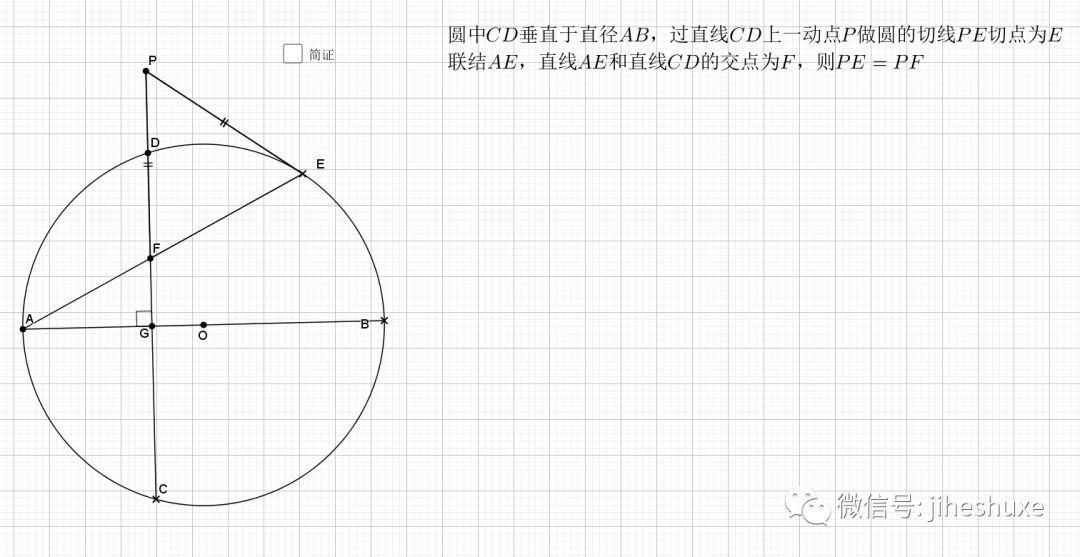 切线其实也是一个垂直的角度条件啊
切线其实也是一个垂直的角度条件啊
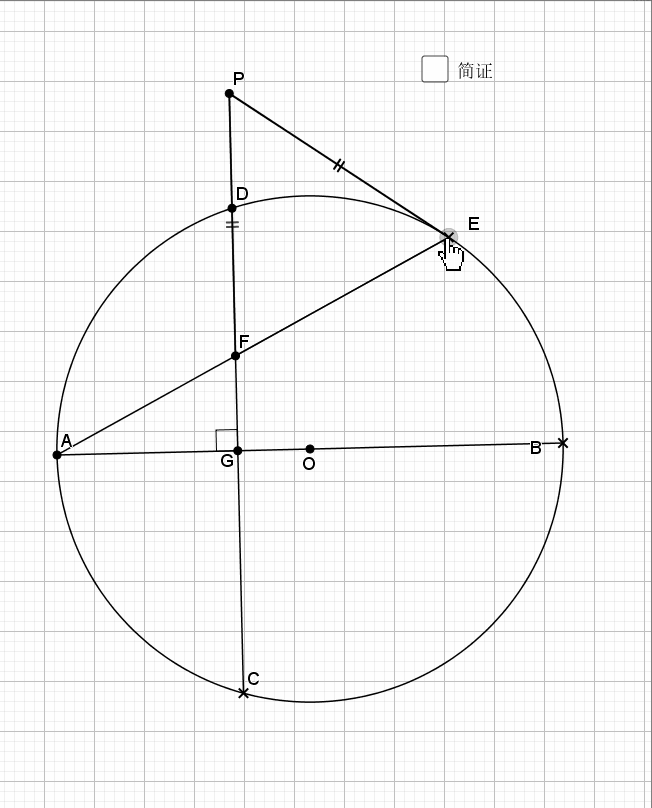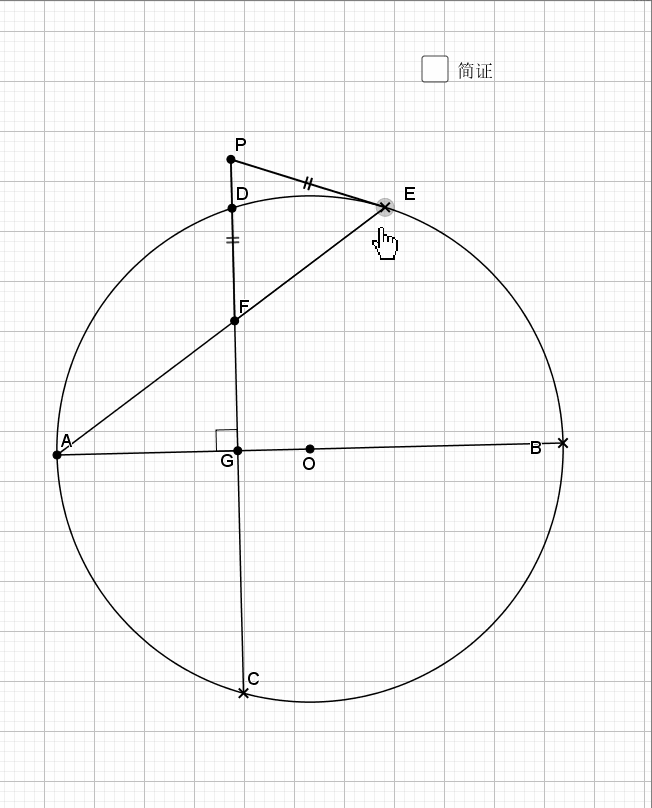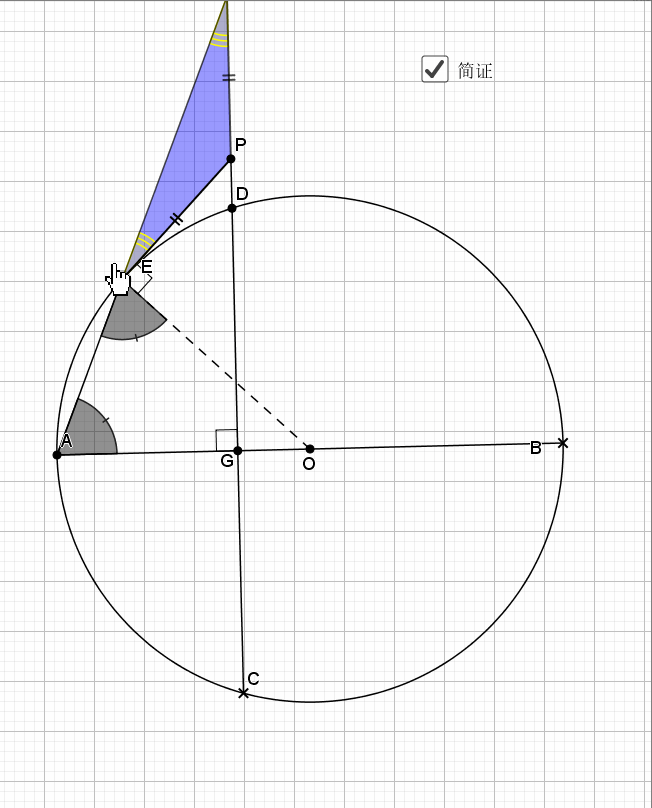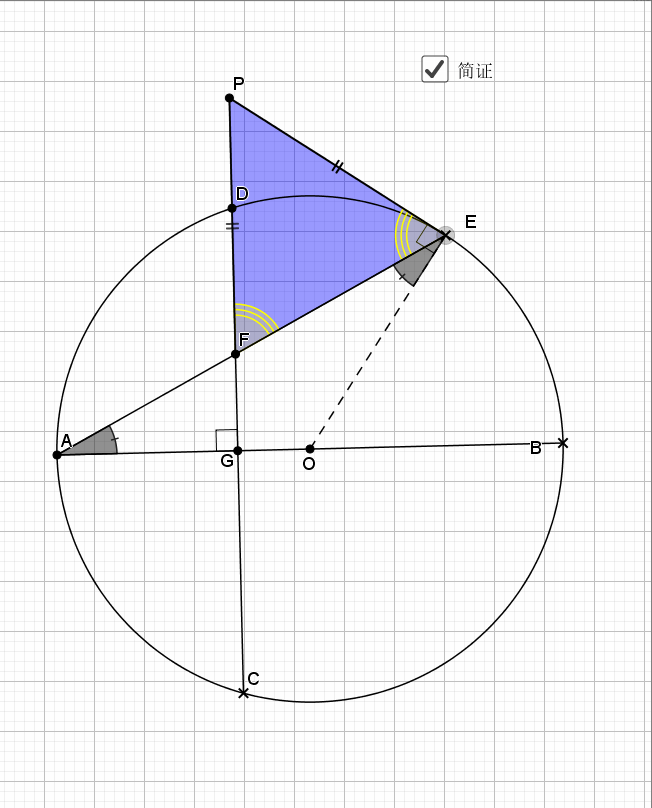
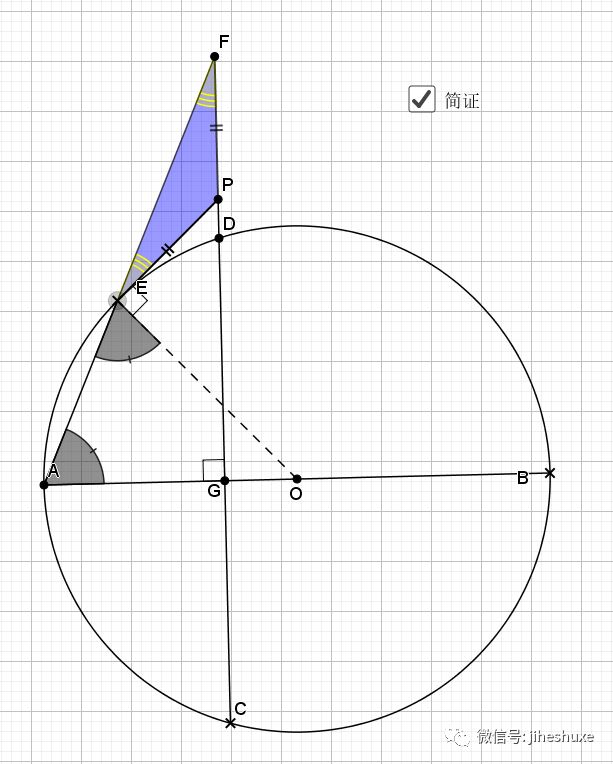
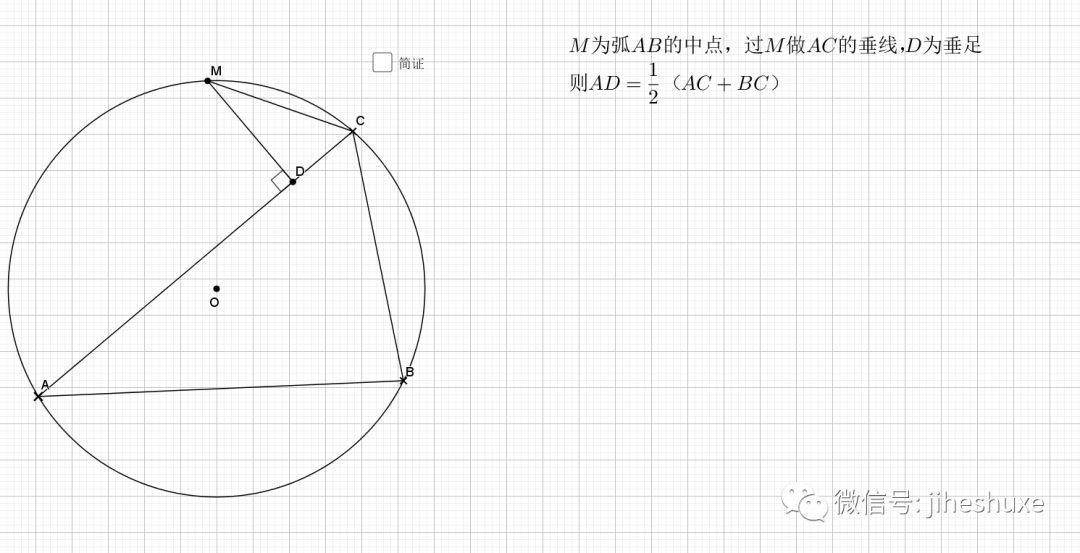 利用了圆中的旋转思路(
延伸阅读:旋转策略,从简单到不简单
)
利用了圆中的旋转思路(
延伸阅读:旋转策略,从简单到不简单
)
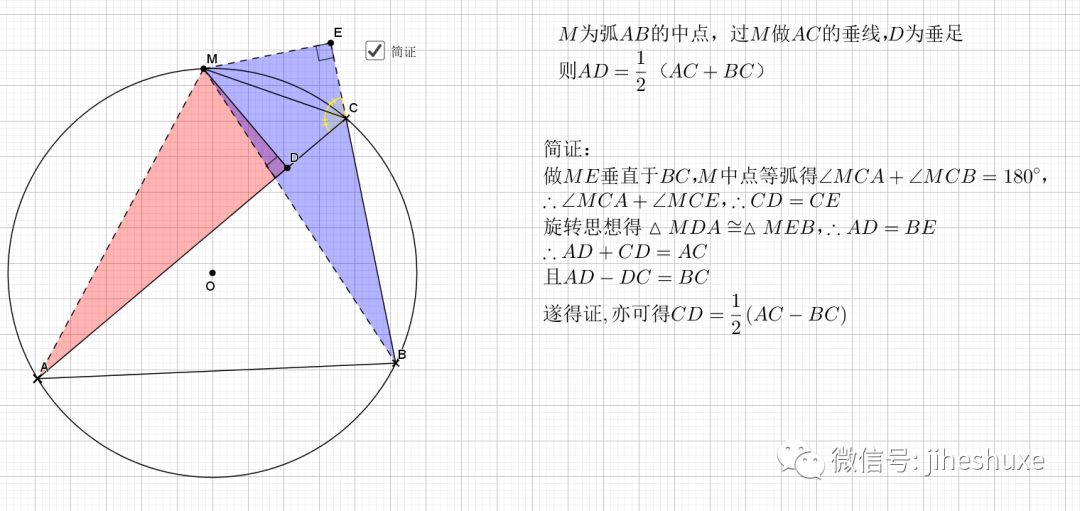
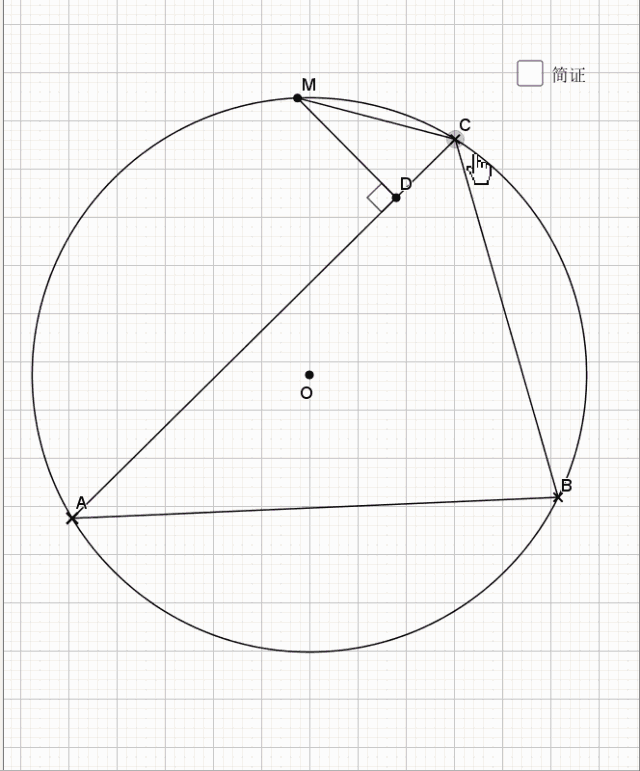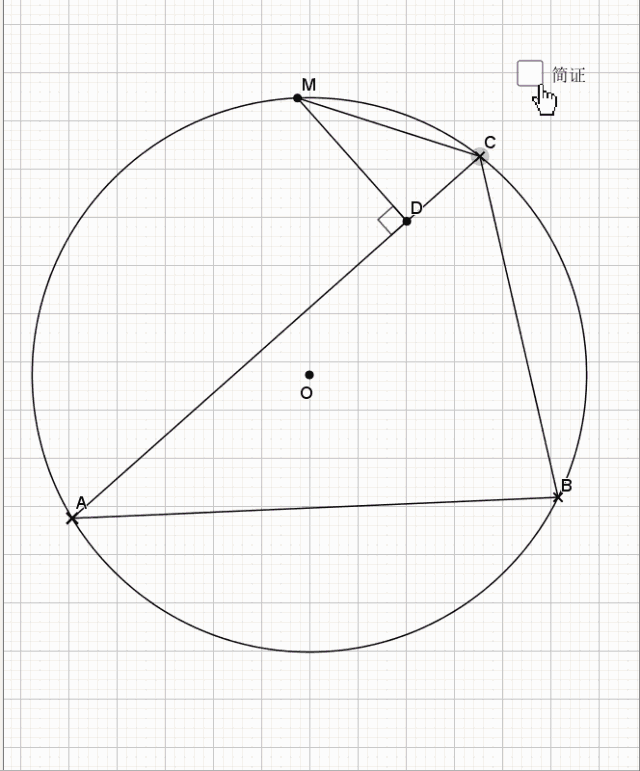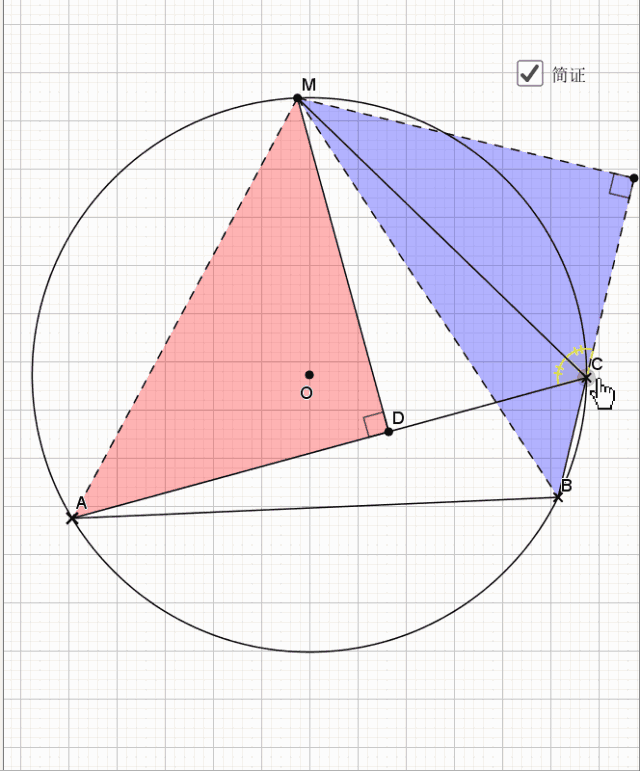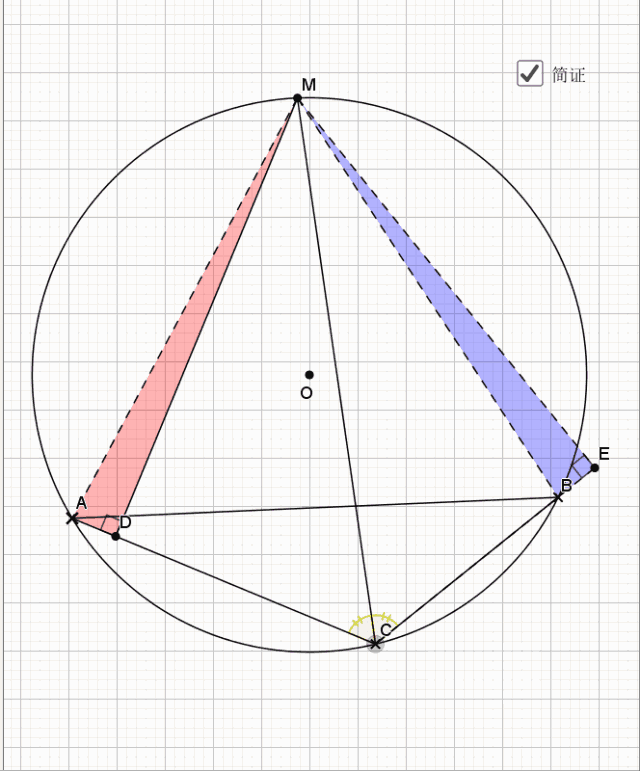
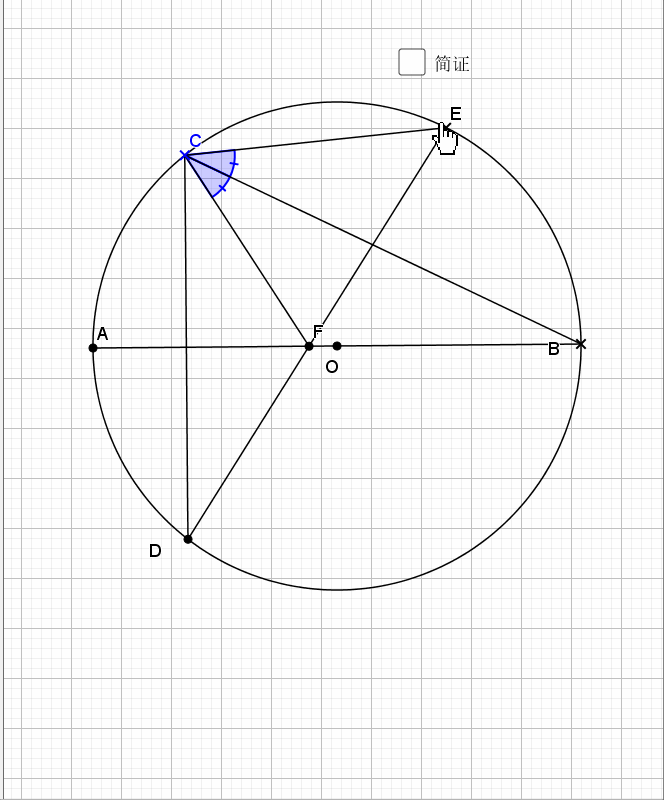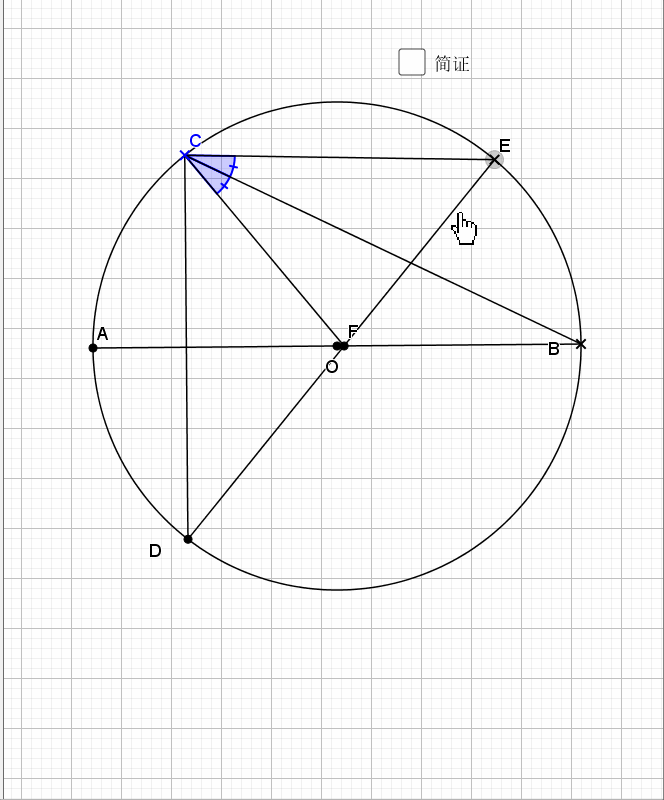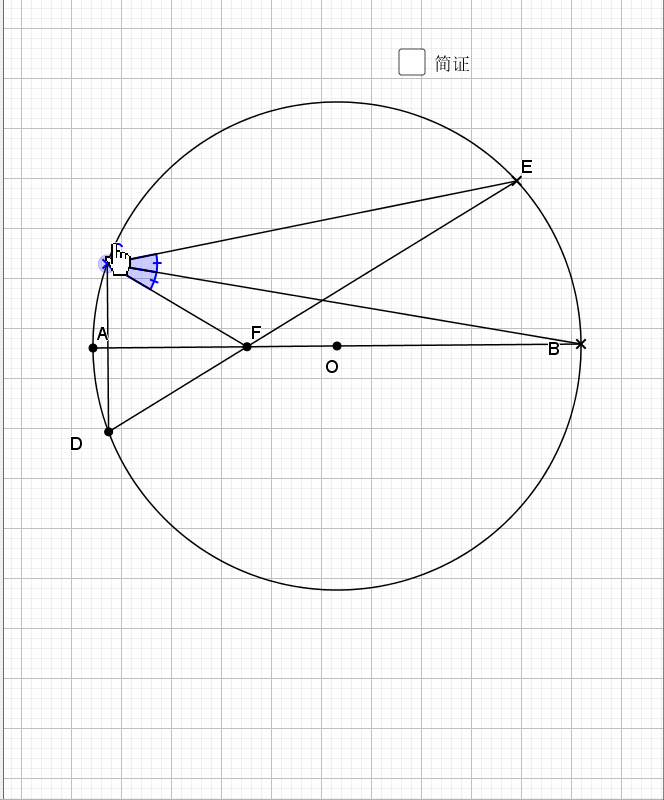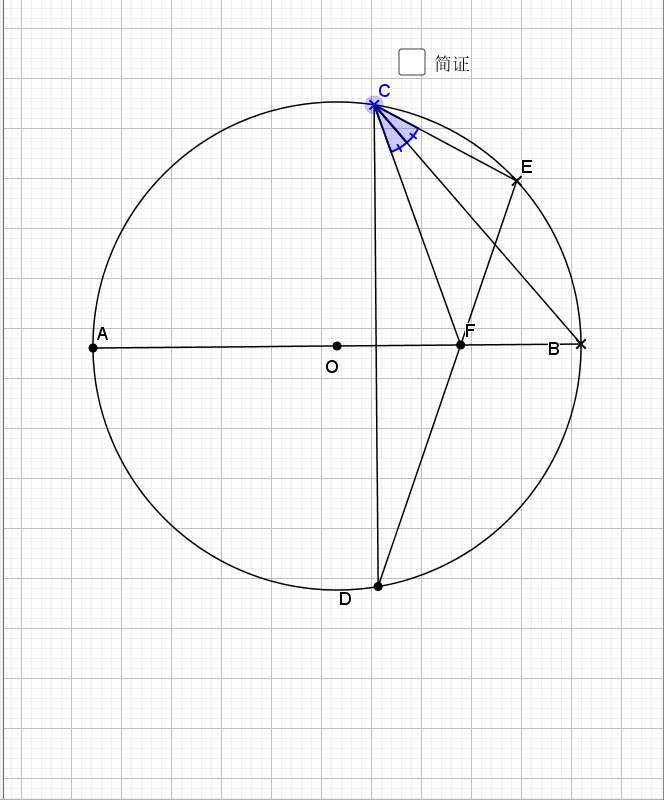
25.垂弦得角平分
简单的一个倒角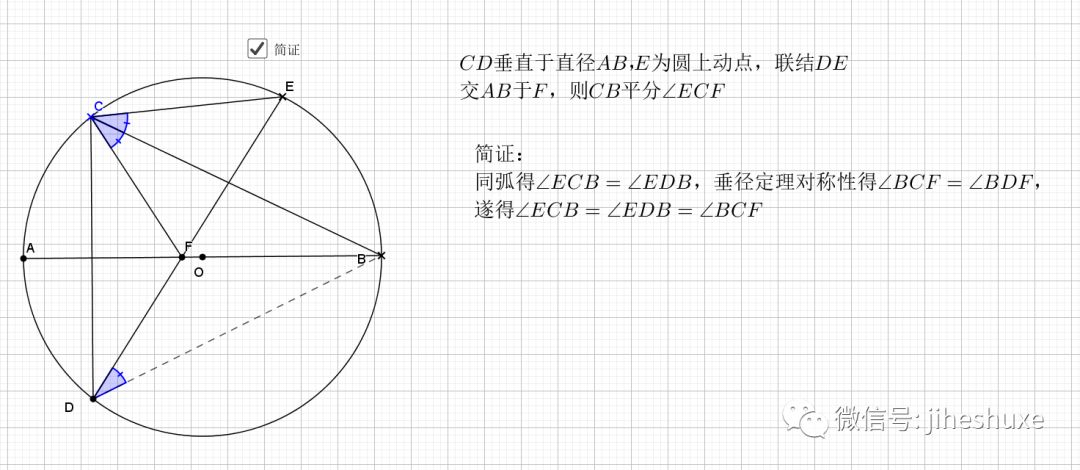
来源:几何数学(ID:jiheshuxue),作者:司凯;如存在文章/图片/音视频使用不当的情况,或来源标注有异议等,请联系编辑微信:ABC-shuxue第一时间处理。

最后,邀您进下方公号学习

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








