bv值是什么意思_11.4 线性值函数几何学

这一节我们介绍几个关于值函数近似误差的概念．进一步的理解离策略，值函数近似的含义．理论上还是比较重要的．最近的一篇文章Deep Residual Reinforcement Learning和这一节的内容关联很大，感兴趣的可以看看．

好了，开始吧

先看看什么叫近似？先假设我们不用近似，那么值函数空间是怎么样的．假如我们有

个状态，每个状态被值函数

映射到一个实数：

．那么所有的值函数就是一个

维的向量，位于

空间中．比如对于一个状态空间

,一个值函数可以表示为：

．而近似就寻找一个子空间来尽量的接近这个值向量空间．但是因为近似值函数的参数少于值向量空间的维度，所以这种近似必然是不精确的。

说起来有点抽象，我们先从一个容易理解的例子开始。

值函数近似

假如我们有个状态空间，包含３个状态

．我们用值函数近似，包含两个参数

．那么每个值函数

可以看成是三维空间中的一个点（值向量空间是三维空间）．而近似的值函数

位于由

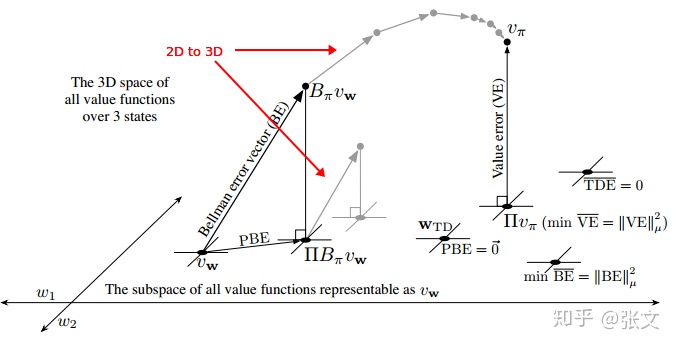
构成的一个二维空间中．如果是广义的近似，那么这个全空间（full space，值向量空间)和可表征的子空间（由参数定义的值函数空间）的关系是很复杂的．但是如果是线性的值函数近似，这个子空间就是一个简单的平面．如下图所示：

图11.3 线性值函数近似的几何特性

这个图还是很博大精深的，建议大家多理解理解．

值误差

对于一个固定的策略，它真实的值函数表示为

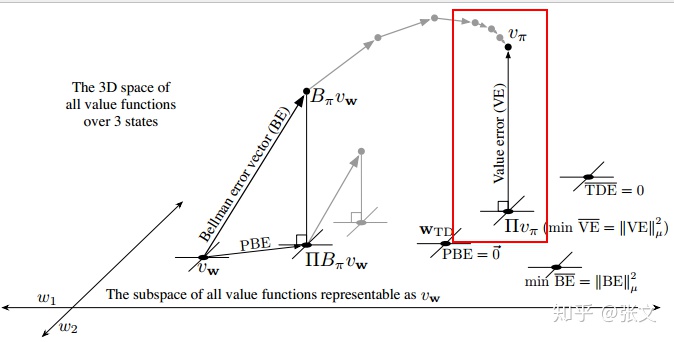
，我们无法用值函数近似来精确的获得它的值，因此它在这个子空间之外，图中右上方所示．如果

不能够精确的表示，那么我们自然会问：最接近它的表征形式是什么？说到接近，就涉及到距离．怎么来衡量两个值函数的距离？给了两个值函数向量

和

，我们可以用向量差

来表示他们的差异．如果

比较小，说明他们比较接近．但是我们如何描述这个差向量的大小呢？传统的方法就是欧几里得范数．但是仅仅是范数是不合适的．因为一个很大的状态空间，我们总是选择专注在某个子空间．有些状态的近似值可能误差很大，但是我们对它没有兴趣，或者说它的值对于策略并没有什么影响，这个时候我们完全可以忽略这个误差．怎么实现这样的效果呢？加权，给每个状态误差一个权重

来表示他们对于误差贡献的大小．那么这个新的加权距离表示为：

一般选择为在策略分布（on-policy distribution)．通过这个定义，9.2节的

值误差可以表示为：

.那么求解距离

最近的子空间表征就是一个投影操作．定义 投影算子

将任意的一个值函数

映射到范数最小的表征函数，即：

那么求解最好的近似函数，就等价求

的投影，如下图红色方框所示．我们可以通过ＭＣ方法得到这个解。怎么理解呢？就是大量的采样得到

。不要问为什么，值函数就是这么定义的。有了真实的

，求投影（最小化值误差）就得到了

。

贝尔曼误差

其实通过前面几章，我们知道除了用MC方法求解

外，还可以用其他方法，比如TD。但是用TD方法会得到一个不同的解．为什么会这样？回忆一下贝尔曼方程：

把

看成是变量，上面等式的精确解就是

．而我们的近似解是

，如果

，那么等式11.13就不成立了，也就是左右不完全相等。而这个差值可以用来衡量

到

的距离．我们称之为*

贝尔曼*误差（Bellman error)：

这说明贝尔曼误差是ＴＤ误差的期望．每个状态的贝尔曼误差构成了一个向量，叫做贝尔曼误差向量．这个误差向量的范数叫做均方贝尔曼误差（mean squared bellman error)：

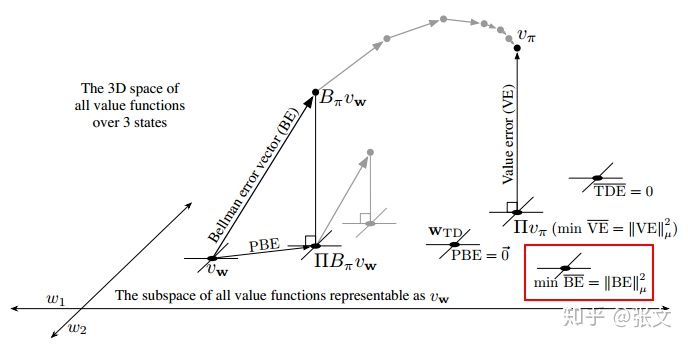
如果说能够把贝尔曼误差降到０，我们其实就得到了真实的

，但是一般情况下我们做不到．但对于线性的情况，我们能够得到一个收敛的

来最小化

．但是这个解和通过VE得到的解不一样．后面两节会讲一些试图最小化BE误差的方法．

投影贝尔曼误差

通过贝尔曼方程，我们可以定义贝尔曼算子为：

那么相应的，贝尔曼误差向量表示为：

．其实也就是进行一次值备份．如果我们对近似值函数做贝尔曼运算，通常会得到一个新的子空间之外的值函数．如果我们重复的在子空间之外对值函数做贝尔曼运算，最终我们会收敛到真实的值函数

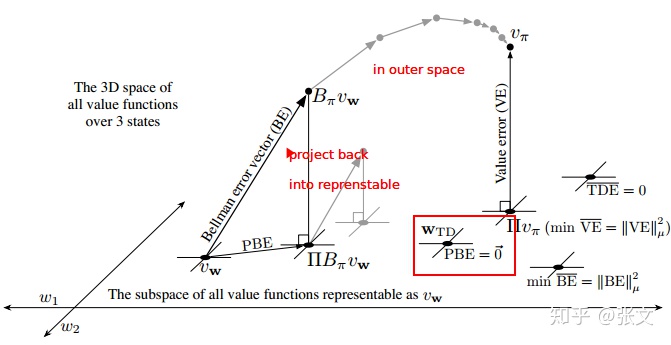
（下图中灰色线条所示）．但是在值函数近似中，我们只能表征子空间中的值函数，对于值空间的函数无法表示．所以我们必须把它投影到子空间里，即从

．这个子空间的值函数经过贝尔曼算子又被带到了子空间之外，然后又被投影回来，如此反复．这个过程中，投影前后两个向量的误差我们称之为

投影贝尔曼误差向量(projected bellman error, PBE)．这个向量的大小又定义了另一个值函数近似的误差测度．叫做均方投影贝尔曼误差（mean square projected bellman error)：

在线性函数近似中，总是可以找到一个值函数，使得

．

总结

其实看这个几个误差，之间也有一些关系．值误差VE是利用类似MC方法得到的近似函数的测度．如果用类似于贝尔曼的更新方式，比如TD方法，就得到了贝尔曼误差测度．贝尔曼误差测度又分两种情况，如果在原空间（值向量空间）执行贝尔曼算子，就是贝尔曼误差BE，它会收敛到最优解．如果用了函数近似，在迭代贝尔曼算子的时候，必须把值函数投影到子空间，这样会得到不同的解．这个误差就是投影贝尔曼误差PBE．

选用不同的误差测度，会影响最终值函数的近似特性，从而影响策略．