分式化简结果要求_期末数学必考题冲刺 ——初一分式化简与分式方程

点击上方蓝字关注，获得更多精彩内容~

分式的化简求值方法是“分式”这一章的解题命脉，特别是“分式的恒等变形”一直是同学们攻克难题的一大障碍！

此外，分式的化简求值也是“代数式恒等变形”的核心之一，它让“整式的恒等变形”告别了单身，两者相得益彰！

分式方程则是“分式”这一章的必考内容，对于初次接触分式方程的同学们而言，困扰大家最多的两个问题，就是“计算技巧”和“增根”的问题，前者往往是由于没有找到正确的思路导致的，而后者则更多地出现在由“增根”确定字母系数的问题上！

为此，优能中学蒋晓濛老师将针对期末考试“分式化简与分式方程”中的一些常考难题进行题型的归纳总结，让大家今后画瓢的时候有葫芦可以参照。话说至此，咱就步入正题吧～

0 1 ☆分式的恒等变形拓展一、分式恒等变形1——分离常数法✚●○

分离常数的方法：将分式拆分，在分子上凑出分母。

标志题型：已知一个分式为整式，求所含字母的取值范围。

二、分式恒等变形 2——消元法✚●○

当要求的分式中出现多个未知数时，可以把其中一个当成已知数，用来表示其他未知数，从 而达到消元的目的。

三、分式恒等变形 3——降次法✚●○

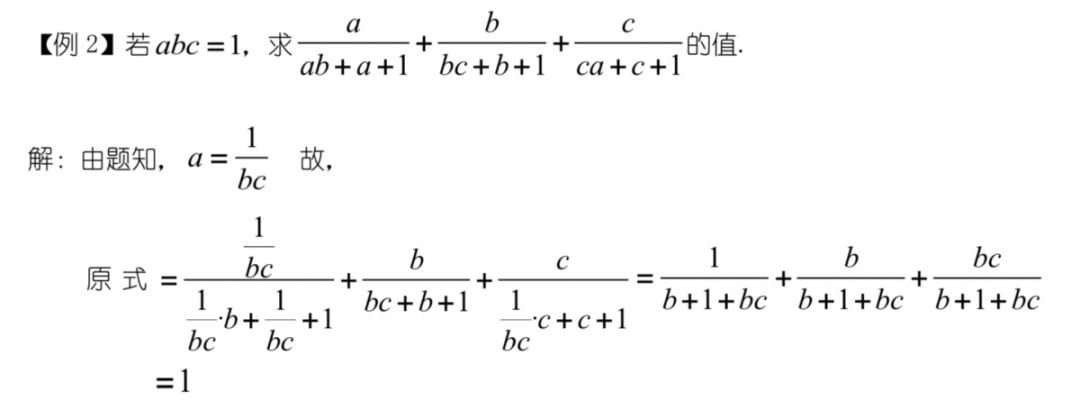
与“消元”相对，若分式中只有一个字母，但出现多种次数，可采用“降次”的策略。

四、分式恒等变形 4——取倒数法✚●○

当分式的分母为多项式，分子为单项式，且不便化简时，可以考虑“取倒数”。

五、分式恒等变形 5——设 K 法✚●○

当遇到连等式时，要直接想到将连等式的结果设为 K ，然后将题目中的其他字母用含 K 的 代数式表示。

六、分式恒等变形 6——反向表示求范围法✚●○

标志题型:求整个分式的取值范围，可以将整个分式设为一个字母，用含这个字母的代数式

来表示原分式中的未知数，从而确定原分式的范围。

0 2 ☆分式方程的基本解法及常见技巧一、基本思想及步骤✚●○

基本思想:化分式方程为整式方程。

具体步骤:去分母 解方程 

检验注:解分式方程一定要有检验的过程，检验的方法是将整式方程的根代入各分式的分母(或 最简公分母)，看结果是否为零，若结果为零，此整式方程的根是原方程的增根，原方程无解;若结果不为零，则此整式方程的根就是原方程的解。

二、常见技巧✚●○

【题目视野拓展来啦!睁大眼睛哦!】

对于形式比较复杂的分式方程，需要通过观察其内部特征，以期找到最佳的解题策略。

常用技巧:换元法、分离常数法、裂项法。

【解题秘籍】:

换元法在整式和分式章节都比较常用，一般情况，当题目中存在“重复部分 反复出现，或者有明显和差或倍数关系的部分出现”等情况时，我们一般会采用换元法。换 元法切记勿忘还原，要灵活运用换多个元。

【注:在解分式方程的过程中，遇到等式两边含有相同代数式的情况时，切不可直接将它们 约去，需要慎重考虑这个代数式是否为零。】

【解题秘籍】:

分离常数法适用于分子分母中都含有字母的分式，并且分子的次数不小于分 母的次数，在特殊方法的分式化简、分式方程和求整数解和求特殊关系解问题中经常使用。

【解题秘籍】:

“分数裂项”是六年级所学的内容，当数向式进行转换时，原来的“分数裂项” 就变为了“分式裂项”，分式裂项的特点是，对分式的分母进行因式分解之后，能直观看出其差是定值，通过六年级所学的(下方)公式，即可迎刃而解。

0 3☆含参数的分式方程

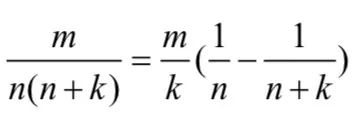
解题思路:

把参数当成已知数，将分式方程化为整式方程的最简形式(或标准形式)，然后 根据根的情况求出参数。

一般情况，含参数的分式方程分为“增根问题、无解问题、特殊关系解问题”等。

真题小试牛刀

同学们，复习之后，咱就利用 40 分钟的时间做四道期末真题，看看你对分式化简和方程的 常用方法是否全部掌握了吧!

名师介绍 蒋晓濛老师

欲获取真题解析答案

请关注下方公众号

回复关键字“分式化简与方程”即可获取哦～