22无限循环注册_π的世界里，还藏着“无限”的思维魅力

无论是喜欢数学，还是不喜欢数学的读者，都对π有一定的了解，也对“无限”略知一二。麦教授想分享的，是由π到无限的思维升级。本文不重概念，更考究逻辑思维的跃升。

这也不是一篇关于数学的文章，却不失数学之美，而数学上的思考，到最后其实是哲学。当年我在麻省理工学院读博时，数学日和π在学校里非常受欢迎。很多科普文章讲 π ，我更想从 π 开始讲 “无限”。

有人说 ，π 里面包含了任何可能想到的固定长度的数字。这种说法可以用电脑验证，任何6位数的密码或11位的电话号码，都可以在 π 里面找到。

目前，我们已经知道了 π 的前22万亿位，只要在前1千4百多万位里，就可以找到所有的6位数字组合。例如，像“520520”这种，或者是我们喜欢的人的6位数字生日。

01

始于“无限不循环”的概念

知道π、根号，和自然对数e的时候，可能是我们最早接触到“无限不循环”这个概念的时间点。当我们知道有些数是无穷无尽的，是根本写不完的时候，我幼小的心灵受到了巨大的震撼。

——为了写这个数，可以要求地球上所有的人一起努力。我们不吃，不喝，不睡觉，从生下来一直写到死，即便“子子孙孙无穷匮也”，也永远都写不完。

那时，小小的我，领悟到一个道理：有时候不管怎么努力都是没有用的。

我最近看一本书时才知道，有个关于 π 的真理。三位数学家在1995年发现了一个公式，叫做Bailey–Borwein–Plouffe formula。

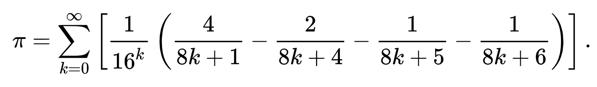
它的厉害之处，是可以计算 π 的第 n 位二进制数 (或者16进制数，有个算法叫Spigot algorithm)。

这很让人震惊。因为之前所有的计算圆周率的方法，都是一位一位地逼近，不知道前面的数字，就没法知道后面的。

正如所有厉害的武功路数一样，这个算法有弱点，当n很大的时候，计算就慢下来，其实还是没法计算到任意位。这让我们认识到一件事：天下有好吃的午餐，但是没有免费的午餐。

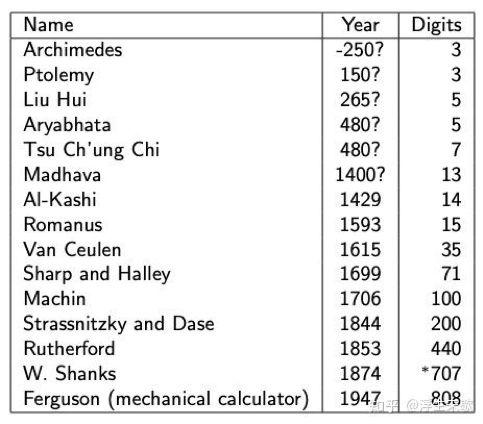
如图，这个表格是计算机发明之前计算出来的π 的位数，中国人刘徽和祖冲之都做出了早期的贡献。

02

无穷大的“无限”

人类看到的和感知到的，没有一样东西是无限的。有些东西换成数字，可以很大，如这个世界存在的时间，又如宇宙中原子的数目。

但这些都是可以被计算出来，物理学过去一百年的进展，让这些数字都可以很精确地确定。后来，数学里出现了“无穷大∞”。

这个符号是17世纪的英国数学家John Wallis发明的，将数字 “8”躺赢，变成无穷大“∞”符号。我们不得不说，他真是天才。说到“∞”符号，或许很多读者未必知道，世上存在一只咬着自己尾巴的蛇。

再说说与无穷大符号很像的莫比乌斯圈。取一张纸条，扭转180度之后，两头再粘起来，这样的纸圈，就是神奇的莫比乌斯圈。

我们可以想象一只蚂蚁沿着莫比乌斯圈爬，它能在不跨越边缘的情况下，爬遍整圈。然后一圈又一圈，回到原点。

莫比乌斯圈是只有一个面的平面，不信你可以用一根笔在上面画蚂蚁爬行的轨迹，笔不用抬起来就可以在这张只有一个面的纸上画满线。

莫比乌斯圈没有边界的概念，看似有双侧曲面，却是一个无限循环的圈。更神奇的，是用剪刀沿着纸带中间，把莫比乌斯圈剪开。本以为是一分为二，两头不再相粘。但剪出来的，反而是一个两倍长度的纸圈。

03

无限大和无限大的比较

后来，我们学了微积分，知道无限大和无限大并不一样大。但是，无限大和无限大的比较，并不是通过谁大谁小来做到的，而是通过比较谁的增长速度快来做到的。

数学里有个著名的洛必达定理，就严格证明了这件事。洛必达其实是个商人，是业余数学爱好者，这个定理不是他发现的，而很可能是他从约翰伯努利那里买来的。

洛必达出身贵族，曾受袭爵衔，未成年就解出帕斯卡的摆线难题。后来，他拜在约翰伯努利门下，钻研微积分，著有《无限小分析》一书，创造出一种能用来求得满足一定条件的两个函数之商的极限算法。

而这本书，多半是伯努利写的。

洛必达去世后，约翰伯努利发表声明，称洛必达定理和有些发现，应是归功于自己。但是来不及了。这个定理现在还是被称为了洛必达定理。

虽然伯努利叔侄三人对数学、统计学的贡献大，不缺这一个定理，但是也还是很遗憾的，谁叫他拿了别人的钱呢。

04

“无限”到底存不存在

最近对“无限”的思考又升级了，其实相对论和量子力学告诉我们，自然界根本就没有无限，也没有连续。“量子”quantum这个词就是“离散”的意思。

我们之前认为大的数字，如光速，其实是有限的，每秒才30万公里(这个速度在宇宙的维度里简直慢透了)！宇宙从诞生到现在，只经历了1017秒！而宇宙中的原子的个数也就是1080左右这么多！

世间最远的距离不是与你擦肩而过，而是宇宙的直径：8.8x1026米(大约930亿光年)。世间最短的距离也不是心与心的碰撞，而是普朗克距离：1.6x10-35米。所以，“无限”这个概念最奇怪的地方，是它根本就不存在！

那条咬自己尾巴的蛇，告诉我们：无限并不是没有尽头，无限的本质是循环往复的。

和许多哲学家一样，我小时候也想过一个悖论。就是我跑100米短跑的时候，总要跑到一半50米的地方，而之后就需要跑到剩下距离的一半，也就是距离终点25米的地方，接着12.5米。

但这样下去，永远有剩下的距离的一半，这样无限地分下去，怎么可能到达终点呢？这个也叫Zeno悖论，几千年前就有人提出来了，后来很多人各自独立都在思考这个问题。

05

Zeno悖论

学过洛必达定律的自然可以说：不用思考，必达必达。从物理上讲，到了普朗克距离就不可分了，所以那个瞬间就到达了。

从数学上讲，无限多个的变得无限小的区间，最终合并起来的长度，可以是有限的。(An infinite number of progressively smaller intervals could nevertheless amount to a finite total interval.)

例如可以很简单证明 1/2+1/4+1/8+…=1

这让我想起另外一个曾经思考过的问题：假设有一盏灯，你控制那个开关，你让灯亮一分钟，这一分钟它是亮的；之后的半分钟里你关掉它，这半分钟它是暗的；之后的1/4分钟里你再打开它，它又亮了。

就这样，你每次开关的时间缩短一半，直到无限(就是说那时候你的手，要无限快的，在开与关之间变换，每次变换之后，下个状态的持续时间，是这次的一半)，那么在无限久的时间之后，这个灯是开着的还是关着的呢？

说回跑百米这件事，你会问，那个最后的瞬间，是怎么达到的呢？即便距离终点只有1.6x10-35米，也可以跑到离终点0.8x10-35米呀？！我来给你一个数学的证明。

06

思维升级：如何抵达终点

我告诉你结论先：0.99999…=1。

也就是当小数点后面有无穷多个9的时候，它就相等于下一个整数。或许你会说：这怎么可能呢？毕竟是没到1呀。数学很严谨的，差一点点也不行。

那我用小学数学证明给你：

1. 我问你1/3是多少，你说0.333… (后面无限个3)
2. 我问你 1/3+1/3+1/3是多少，你说是1呀。
3. 那0.333…+0.333…+0.333…是多少，。。。。啊，竟然是0.999…

这个证明告诉我们另外一个有正能量的道理：你如果真的努力了，虽然你觉得永远到不了终点，但是你已经到终点了。我刚刚说过世间没有无限，但是问一个简单的问题，一片雪花的周长有多长？

这个问题涉及分形理论，是数学家Mandelbrot整出来的 (如下图，值得一提的是：他有一段时间研究股票市场，做出了非常厉害的贡献，但是他很快就回去研究分形理论了，所以金融市场的理论，现在还这么弱。

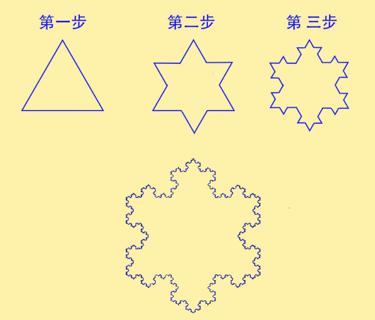
这就是一个最简单的雪花图形(Koch曲线)：

1. 最开始是一个等边三角形；
2. 然后在等边三角形的三条边上，分别长出一个小一点的等边三角形，小三角形的边长是原来三角形的1/3；
3. 此后，每增加一步，都在上一步增加的三角形上，长出前三角形边长1/3的等边三角形，直到无限。

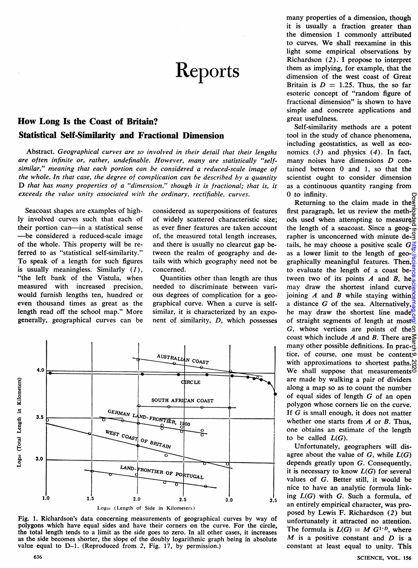
可以算出来这样的最终的雪花的周长，是无限的！而它的面积又是有限的。画一个圆就圈住他。

1964年，Mandelbrot问英国的海岸线有多长，且在Science上发表相关文章。如果不是有普朗克距离做最小的尺子，英国海岸线的长度，也是无限的！

有人说过，让无数只猴子坐在打字机前，随机敲击键盘，如果不限定时间，那么它们总有一天会打出一部《莎士比亚全集》。

其实不用猴子，前面说过 π 里面包含了任何可能想象的固定长度的数字。如果用ASCII码表示英文字母，《莎士比亚全集》的长度是固定的，所以一定可以在 π 里面找到《莎士比亚全集》！

而且不仅仅是《莎士比亚全集》，任何人类历史或未来写出来的东西，包括麦教授现在这篇文章，都可以在 π 里面找到！ 不止能找到，还能找到无限多次，这不就是在不循环中出现的循环吗？

这就是“无限”的魅力吧。