Codeforces 903D Almost Difference

题意：

定义一个函数

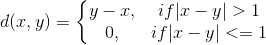
给定一个含有n个数的数组a，要求求出所有d(ai,aj)的和，其中1<=i<=j<=n。

其中1<=n<=2e5，1<=ai<=1e9。

题解：

虽然ai最大为1e9，但最大也就只有2e5个数，因此可以先离散化再建线段树。线段树里每个节点存有数的和还有数的个数。遍历每个数，对于当前的这个数ai，求出比它小的数的和sum和个数count，则count*ai-sum加到结果里，其中注意ai在线段树的前一个叶子节点是不是ai-1，是的话要把这个点忽略掉。接着求出比它大的数的和sum和个数count，接下来同理。最后累加得到的就是结果。结果会爆longlong，可以用long double，但是注意一下输出格式。

#include<bits/stdc++.h>
using namespace std;
#define ls t<<1
#define rs (t<<1)|1
const int MAXN=200010;
const int MAXN1=2001000;
const int INF=0x3f3f3f3f;
typedef long long ll;
typedef long double ld;

int n,cnt;
ll a[MAXN],b[MAXN];
map<ll,int> ma;

int fa[MAXN];

struct NODE
{
    int left, right,lazy,sum;
    ld val;
}tree[MAXN1];

void build(int left, int right, int t)
{
	tree[t].left = left;
	tree[t].right = right;
	tree[t].val = tree[t].lazy = tree[t].sum=0;
	if (left == right)
	{
		fa[left] = t;
		return;
	}
	build(left, (left + right) / 2, ls);
	build((left + right) / 2 + 1, right, rs);
}

void update1(int t)
{
	if (t == 1) return;
	t = t / 2;
    tree[t].val = tree[ls].val + tree[rs].val;
    tree[t].sum=tree[ls].sum+tree[rs].sum;
	update1(t);
}


ld queryVal(int left, int right, int t)
{
	ld sum = 0;
    if (tree[t].left >= left&&tree[t].right <= right)
		return tree[t].val;
	int mid = (tree[t].left + tree[t].right) / 2;
	if (left <= mid) sum += queryVal(left, right, ls);
	if (right > mid) sum += queryVal(left, right, rs);
	return sum;
}

int querySum(int left, int right, int t)
{
	int sum = 0;
    if (tree[t].left >= left&&tree[t].right <= right)
		return tree[t].sum;
	int mid = (tree[t].left + tree[t].right) / 2;
	if (left <= mid) sum += querySum(left, right, ls);
	if (right > mid) sum += querySum(left, right, rs);
	return sum;
}

int main()
{
 //   freopen("input.txt","r",stdin);
 //   freopen("output.txt","w",stdout);

    ios_base::sync_with_stdio(0); cin.tie(0);
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        cin>>a[i];
        b[i]=a[i];
    }
    sort(b+1,b+1+n);
    for(int i=1;i<=n;i++)
    {
        if(ma.find(b[i])==ma.end()) 
        {
            cnt++;
            ma[b[i]]=cnt;
        }
    }

    build(1,cnt,1);
    ld ans=0;
    for(int i=1;i<=n;i++)
    {
        int ord=ma[a[i]];
        tree[fa[ord]].val+=a[i];
        tree[fa[ord]].sum++;
        update1(fa[ord]);
        ll val;
        int sum;
        if(ord!=1) 
        {
            if(ma.find(a[i]-1)==ma.end()) 
            {
                val=queryVal(1,ord-1,1);
                sum=querySum(1,ord-1,1);
                ans+=sum*a[i]-val;
            }
            else 
            {
                if(ord!=2)
                {
                    val=queryVal(1,ord-2,1);
                    sum=querySum(1,ord-2,1);
                    ans+=sum*a[i]-val;
                }
            }
        }
        if(ord!=cnt)
        {
            if(ma.find(a[i]+1)==ma.end()) 
            {
                val=queryVal(ord+1,cnt,1);
                sum=querySum(ord+1,cnt,1);
                ans+=sum*a[i]-val;
            }
            else if(ord!=cnt-1)
            {
                val=queryVal(ord+2,cnt,1);
                sum=querySum(ord+2,cnt,1);
                ans+=sum*a[i]-val;
            }
        }
    }

    cout << fixed << setprecision(0) << ans << endl;

    return 0;
}