一、图结构
图:描述关联数据的通用语言。在图中,节点之间是有关联的。但在传统机器学习中,数据样本之间独立同分布。

图需要兼容任意尺寸(不定长)的输入结构和复杂的拓扑结构,且没有参考锚点(不像CNN和GNN有一个处理的起点)。且图也是动态变化的和多模态的特征(不同类型)。
二、图的表示
图由以下内容组成:节点(nodes),记作N;边(edge),记作E;全图(graph),记作G(N,E)

在设计图之初,我们需要制作一个本体图(将事物及其可能产生的联系做成一张图);
本体图的设计应遵循以下要求:①本体图必须是唯一的、无歧义的;②节点可能含有多种不同的数据类型;
1.图的属性
一般的图可以分为无向图(对称的、双向的)和有向图。

除此之外,还有一种被称为异质图(heterogeneous graph),这种图中可能包含多种节点和多种连接,记作G=(V,E,R,T),若一张异质图中存在两种节点则被称为二分图(Bipartite graph)。


将二分图中的两种节点展开即可生成展开二分图(Folded networks)

具体的展开方式为:将二分图的不同种类的节点分开;并根据二分图的连接,为得到的两张新图添加新的连接。
节点的连接数/度
如下图(无向图)中的A节点的![]() ;一张图的平均连接数是
;一张图的平均连接数是![]() (一条连接对两个节点都贡献有度,固需要x2)
(一条连接对两个节点都贡献有度,固需要x2)

对于有向图而言,需要区分in-degree和out-degree。如下图中的C节点,![]() ,
,![]() ,而整体degree=in-degree + out-degree(
,而整体degree=in-degree + out-degree(![]() )
)
当一个节点的in-degree=0时,称Source;当out-degree=0时,称Sink;平均连接数![]() 且由于
且由于![]() 和
和![]() 一一对应,所以in-degree的平均与out-degree的平均是一致的
一一对应,所以in-degree的平均与out-degree的平均是一致的

除了一般的不带权重图,还有一种图的连接是带权重的,称为带权重图。带权重图的邻接矩阵的元素为其边的权重,不再是非1即0。权重图的读数是所有非0元素求和再除以连接数

当图存在自输入(self-loops)时 ,邻接矩阵的主对角线元素不再为0。其连接数需要额外加上主对角线元素(不再除2)

当图中存在多重连接(Multigraph)时,邻接矩阵的元素等于该点的连接数相加。

图的连通性
图中必定存在一条通路(可能不止一条),使任意两个节点之间可以触达/连通。这个范围称为:连通域(Connected components)
若两个点之间不连通,则其邻接矩阵将呈现“分块对角”的性状

当这两个图之间出现连接则会打破这种性状
对于有向图而言,若任意两个结点可以通过有向连接相互触达,称为:强连接图,如下图中由ABC三个节点构成的子图就是一个强连接图,又称强连通域(Scc),指向Scc的节点称为In-Component(如E、G)、从Scc中指出的节点称为Out-component(如D、F);而仅在忽略方向的情况下相互连通称为:弱连接图,下图全图是一个弱连接图。

2.图的矩阵表示
①邻接矩阵
一般采用邻接矩阵表示。当节点i和节点j之间存在连接时,矩阵中的![]() ,若没有连接,则Aij=0
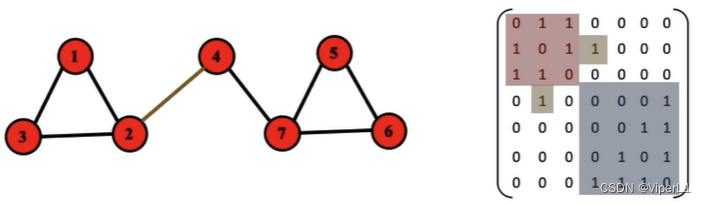
,若没有连接,则Aij=0![]() 。如下图可以表示为:
。如下图可以表示为:

当图为无向图时,邻接矩阵为对称矩阵,且主对角线为0(无自输入连接时);某个点的连接总数等于沿该点的行/列求和。
而对于有向图来说。邻接矩阵不再是对称矩阵,![]() =节点列之和,
=节点列之和,![]() 节点行之和
节点行之和

但实际上大部分自然世界的连接都是稀疏矩阵(大部分都不存在连接)。这种时候则可以采用连接列表和邻接列表来表示。

②连接列表
连接列表的具体做法为:使用一个数组,仅记录存在连接的节点对,表示如下:
(2,3) #有一条边由节点2指向了节点3
(2,4) #有一条边由节点2指向了节点4③邻接列表
邻接列表的具体做法为:使用一个数组,将所有与某节点有联系的结点全部列在其后方,表示如下:
2:3,4 #节点2指向节点3,节点4
3:2,4 #节点3指向节点2,节点4


























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








