Backpropagation for a Linear Layer 是李飞飞大牛学生Justin Johnson(注意断句),点击可以看他的个人主页发表的论文涉及了多个领域,博士期间在CVPR/ICCV/ECCV顶会上发表多达13篇论文。本文是他为cs231n课程撰写关于Backpropagation的notes,也是我迄今为止见过最简洁,数学推理比较完备的一篇notes。
在本篇笔记中主要是在线性层中推导反向传播的公式,使用Mini-batch。
在前向反馈中,线性层有一个大小是 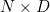 的输入
的输入  ,以及一个大小是
,以及一个大小是 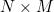 的矩阵
的矩阵 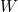 。
。
通过两个输入的矩阵内积计算出大小是 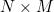 的输出
的输出 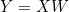 。
。
为了让这个例子更具体,我们令 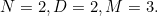 现在我们以这个例子可以写出前向传播的输入:
现在我们以这个例子可以写出前向传播的输入:

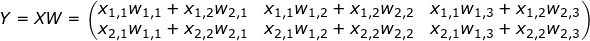
在前向传播后,我们假设输入会在网络的其他部分被使用,最后被用来计算损失  。
。
在反向传播中,我们假设它的导数(实际上是偏导)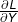 已经被计算出来。比如说如果线性层是线性分类器的一部分,那么矩阵
已经被计算出来。比如说如果线性层是线性分类器的一部分,那么矩阵 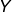 给出了分类的打分;这些分数被喂到了损失函数中(例如SVM中的softmax),用来基于打分scores计算损失
给出了分类的打分;这些分数被喂到了损失函数中(例如SVM中的softmax),用来基于打分scores计算损失  和 导数
和 导数 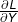 。
。
当  是矩阵
是矩阵 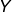 的一个标量,大小为
的一个标量,大小为 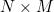 。梯度
。梯度 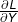 会使一个矩阵并且和矩阵
会使一个矩阵并且和矩阵 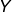 的大小一样都是
的大小一样都是 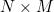 。并且梯度
。并且梯度 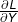 的每一个元素都给出了损失
的每一个元素都给出了损失  基于矩阵
基于矩阵 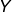 的每一个元素的导数
的每一个元素的导数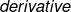 :
:
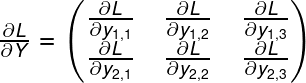
在反向传播中,我们的目标是使用partial 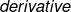
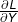 来计算
来计算 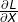 和
和 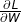 。并且,当损失
。并且,当损失  是标量时,
是标量时, 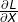 大小必须是
大小必须是 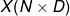 ,
, 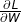 大小必须是
大小必须是 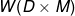 。
。
通过链式法则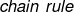 ,我们有(Goal):
,我们有(Goal):

上式中 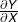 和
和 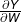 称为雅可比矩阵
称为雅可比矩阵 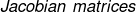 ,包含矩阵
,包含矩阵 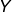 的每一个元素基于输入
的每一个元素基于输入  和
和 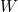 每一个元素的偏微分
每一个元素的偏微分 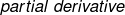 。
。
然而我们不想单独对 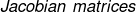
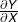 和
和 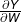 单独计算,因为我们知道他们会非常大。在经典的神经网络中,我们大概率有
单独计算,因为我们知道他们会非常大。在经典的神经网络中,我们大概率有 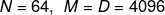 ,然后我们的
,然后我们的 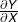 包含了
包含了 个标量值。(这足够有680万个数,使用32位的浮点数,这个
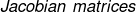 会占据256G的存储空间)。因此需要额外单独存储
会占据256G的存储空间)。因此需要额外单独存储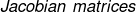 矩阵。
矩阵。
但是我们对于大多数常见的神经网络层,我们的导数计算  时不需要单独计算
时不需要单独计算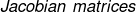
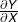 。甚至我们连
。甚至我们连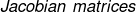
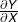 也不需要单独计算;在许多场景中,我们只需要算出小样例的数据,然后在内部进行推导。
也不需要单独计算;在许多场景中,我们只需要算出小样例的数据,然后在内部进行推导。
让我们看看这个如何对我们的例子来计算。
设置 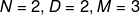 ,首先我们固定
,首先我们固定 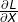 ,然后我们知道
,然后我们知道 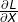 和
和 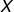 大小相同。
大小相同。

对上式中每一项,首先我们计算 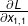 ,通过链式法则,我们知道:
,通过链式法则,我们知道:

上式我们可以知道 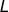 和
和 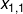 都是标量,所以
都是标量,所以 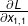 也是一个标量。如果我们看见
也是一个标量。如果我们看见 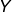 不是一个矩阵,而是由多个标量组成的集合,我们可以使用链式法则来单独计算标量导数
不是一个矩阵,而是由多个标量组成的集合,我们可以使用链式法则来单独计算标量导数 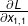 。
。
为了避免求和,更方便来收集所有的 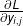 变成一个单独的矩阵
变成一个单独的矩阵 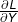 ,这里的
,这里的 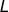 是一个标量,
是一个标量,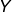 是一个矩阵,
是一个矩阵,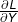 的大小也是和
的大小也是和 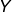 一样的
一样的 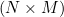 ,
,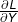 给出了
给出了 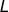 基于
基于 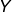 的每一个元素的导数。我们再简单的收集所有的
的每一个元素的导数。我们再简单的收集所有的 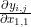 变成
变成 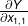 ;因为
;因为 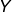 是一个矩阵
是一个矩阵 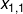 是一个标量,
是一个标量,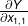 大小也是和
大小也是和 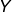 一样的
一样的 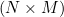 。然后将
。然后将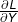 和
和 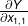 做点乘。
做点乘。
接下来我们有 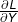 ,然后我们只需要计算
,然后我们只需要计算 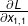 ,我们简单从
,我们简单从 计算微分:
计算微分:
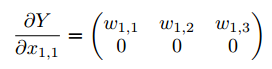
综合上面两个式子,我们重新得到 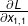 :
:

然后继续重复计算 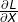 ,其他三个元素:
,其他三个元素:

最后我们综合上面4个元素 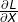 的运算,给出
的运算,给出 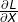 基于
基于 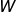 和
和 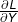 的式子:
的式子:

在式子24中,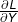 大小是
大小是 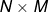 ,矩阵
,矩阵 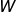 大小是
大小是 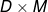 ;尽管最终
;尽管最终 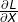 大小是
大小是 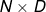 ,它同样和X大小相同。
,它同样和X大小相同。
同理使用相同的原则,我们得到 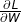 :
:

这种每次只考虑一个元素的策略可以帮助推导出一个层的反向传播方程,即使该层的输入和输出是任意形状的张量;这在推导卷积层的反向传播时尤其有价值。
CSDN的latex格式我还在摸索,有时候有花体时候会用别的字体,有强迫症的朋友抱歉了lol~



























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








