《概率论与数理统计》第四版 浙江大学第1-5章复习

概率论的基本概念

• 统计规律性：在大量重复实验或观察中所呈现出的具有固定规律性
• 随机现象： 自然界有确定性现象和随机现象，随机现象指个别实验中结果呈现不确定性，在大量重复实验中其结果又具有统计规律性，

概率论和数理统计事研究和解释随机现象那个统计规律性的一门数学学科

1.随机实验

通过随机实验是研究随机现象

随机实验特点：

• 可重复性
• 可观察性
• 不确定性

2.样本空间、随机事件

样本空间：随机实验E的所有可能结果组成的集合称为E的样本空间,记为S.样本空间的元素，即E的没个结果称为样本点。

进行随机实验时，人们常关心满足某种条件的哪些样本点所组成的集合。

实验E的样本空间S的子集为E的随机事件，简称事件。在每次实验中，当且仅当这一子集中的一个样本点出现时，称这一事件发生。

有一个样本点组成的单点集，称为基本事件，样本空间包含所有的样本点，是S自身的子集，总是发生的称为必然事件，空集作为样本空间子集，每次都不发生，称为不可能事件

事件是一个集合，因而按照事件间的关系与事件的运算自然按照集合论中集合之间的关系和集合运算来处理。

图形表示：

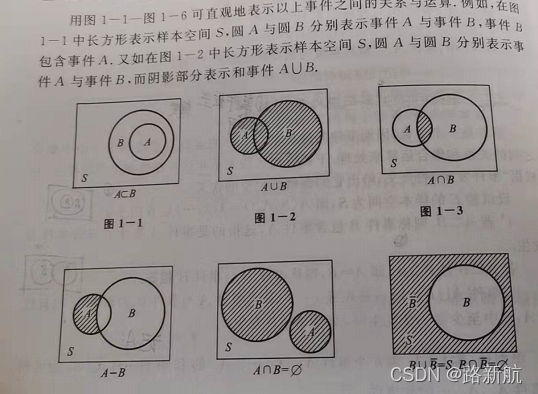
进行事件运算时，常用到下述定律，设A,B,C为事件。
交换律 ：

结合律：

分配率：

3.频率与频数

频率描述了事件发生的频繁程度，进而引出表征事件在一次实验中发生的可能性大小的数-概率
频率：

概率：


重要性质：
i

ii 有限可加性

iii

iv

v逆事件概率

vi 加法公式

4.等可能概率/古典概率

• 实验的样本空间只包含有限个元素
• 实验的每个基本事件发生的可能性是相同的

超几何分布概率公式：

5.条件概率

条件概率

乘法定理

全概率公式

贝叶斯公式

6.独立性

随机变量及其分布

定义：设随机实验的样本空间为S={e},X=X(e)是定义在样本空间S上的实值单值函数，称X=X(e)为随机变量。

离散型随机变量：全部可能取到的值为有限个或可列无限多个

分布律：

0-1分布：
设随机变量X只取0与1两个值，它的分布律是
P(X=k)=p^k * (1-p)^(1-k)

则称X服从以P为参数的（0-1）分布或两点分布。

伯努利实验、二项分布

随机变量X服从n,p的二项分布，记为X-b(n,p)

泊松分布：

随机变量的分布函数
分布函数：

连续型随机变量，概率密度

均匀分布：

指数分布：

正态分布：

对于标准正态分布，引入a分为点定义。

随机变量函数的分布：

定理

多维随机变量及其分布

二维离散型随机变量/联合分布律：二维随机变量全部可能取到的值是有限对，或可列无限多对。

(X,Y)连续型的二维随机变量，函数f(x,y)称为二维随机变量（X,Y）的概率密度，称为随机变量X,Y的联合概率密度。

边缘分布：

边缘概率密度：

随机变量的数字特征