3.5 Domain-Based Consistencies Stronger than AC

存在局部一致性，允许修剪比弧一致性更多的值，同时保持约束不变（与基于约束的k-一致性和一致性所做的相反 - 参见第3.4节）。 我提出的第一个是我们可以应用于变量三元组的不同推理。 其他涉及变量的整个邻域或在单个赋值变量后检查整个网络的局部一致性。

3.5.1 Triangle-Based Local Consistencies

这里定义的局部一致性仅限于二进制归一化网络。 它们都处理约束的“三角形”，即通过二元约束二乘二连接的变量的三元组。这一系列研究之后的第一个局部一致性是Berlandier [13]提出的限制路径一致性（RPC）。 RPC的动机是消除比弧一致性更多的不一致值，同时避免路径一致性的成本。 路径一致性会删除无法扩展到第三个变量的所有值对。 RPC的想法是尝试仅扩展那些值，如果删除，将导致值的弧不一致。 因此，除了弧一致性之外，RPC还保证了值对（（xi，v i），（xj，v j））的路径一致性，它们是对cij（xi，v i）的唯一支持。 如果配对路径不一致，则其删除将导致（xi，v i）的弧不一致。 因此（xi，v i）可以被删除。 这些少数额外的路径一致性检查允许检测比弧一致性更多的不一致值，而不必删除任何值对，因此保持网络结构不变。

RPC严格地比AC强。在图3.5中显示了一个网络，其中RPC修剪的值多于AC。 Berlandier在中提出了算法。 在二进制规范化网络上实现RPC的最佳复杂度是，其中c是变量的三元组数（x，xj，xk），其中cij，cjk和cik都在C中。 这个最佳时间复杂度由Debruyne和Bessiere [42]提出。

在[57]中，Freuder和Elfe提出了其他替代方案来强制执行比AC更强的局部一致性，而仅修改域。 我们的想法是采用k-consistency所做的逆。 k-一致性（或（k-1,1） - 一致性）确保任何大小为k-1的本地一致实例可以扩展到一致的任何第k个变量。 这简单地显示了对于这个属性无法实现的所有实例化。 k-inverse一致性确保大小为1的任何本地一致实例可以一致地扩展到任何k -1个附加变量。 这是（1，k-1）一致性。 由于2  - 逆一致性与2  - 一致性相同，因此最简单的非平凡的这种逆一致性是3  - 逆一致性，或路径反向一致性（PIC），如[57]中所述。

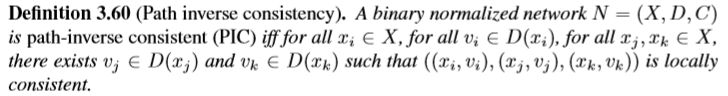
PIC严格强于RPC。 图3.5显示了PIC修剪比RPC更多值的网络示例。 Freuder和Elfe在O（en2d4）中提出了一种算法。 在[41]中，Debruyne提出了一些有效的条件，即网络的路径反向一致性。 他们允许避免一些约束检查。 Debruyne提出了一种在O（en + ed2 + td3）中运行的PIC的最优算法。

在RPC和PIC之后，Debruyne和Bessiere提出了最大限制路径一致性（maxRPC）[42]。 maxRPC仍然增加了变量三角形的局部一致性。 给定值（xi，v i）和约束cij，maxRPC确保（xi，v i）在cij路径上具有对任何第三变量一致的支持。

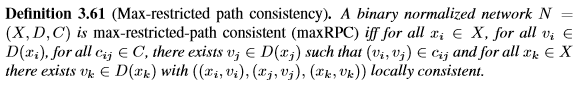
maxRPC严格强于PIC。 图3.6显示了maxRPC修剪比PIC更多值的网络示例。 在[42]中提出了maxRPC的最优算法。 它在O（en + ed2 + td3）中运行。

3.5.2 Consistency According to the Neighborhood

由于k-逆一致性是指数取决于k的多项式，如果k很大，则检查k-逆一致性是禁止的。 但是，如果变量不是统一约束的，那么将k-逆一致性的水平调整到它们的邻域的大小是值得的，将重点放在最受约束的变量上（如在自适应一致性中所做的那样 - 参见3.4节）。2）。 这是邻域反向一致性的基础（NIC，[57]），它确保域D（xi）中的每个值vi可以一致地扩展到xi的所有邻居。

在[57]中提出了一种NIC算法。 它以O（g2（n + ed）dg + 1）运行，其中g是相关超图中变量的最大程度。 它没有被证明是最佳的。 无论如何，似乎难以低于指数因子nd·dg，因为必须证明每个变量的每个值都与其邻域（可能是g的大小）一致。 NIC严格比maxRPC强。

NIC网络不具备自适应一致性网络所具有的无回溯搜索的良好特性。 虽然实现NIC在最大邻域的大小是指数级的，但它既不保证无回溯搜索也不保证网络的一致性。 此外，NIC的行为取决于网络的结构。 如果两个变量xi和xj不是邻居，则通过添加通用约束而获得的网络允许xi和xj之间的所有值对（vi，vj）∈D（xi）×D（xj）等于初始值。 但是，与其他本地一致性相反，NIC会受到此更改的影响，因为xi的邻居已发生变化。 NIC可以检测到更多不一致的值。 显然，这个过程增加了时间的复杂性，因为邻域的大小增加了。

3.5.3 Singleton Consistencies

已经在自动推理的若干领域中使用的一般技术在于依次尝试将不同的值分配给变量，并且对通过该分配获得的子问题执行约束传播。 如果发现问题不一致，则意味着该值不属于任何解决方案，因此可以进行修剪。 这种技术用于调度中的区间域的界限（[90]中的'剃须'）或连续的CSP（[83]中的3B-一致性）。 在[52,85]中，这种技术也用于文字作为在DPLL中为SAT公式推导出更好的变量排序启发式的方法（通过计算文字和单位传播实例化后剩余子句的大小）。 最后，它在[43,102,44]中以“单身一致性”的名义被形式化为一类局部一致性。

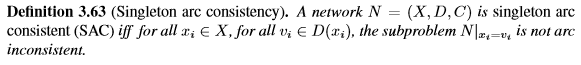
（btw，感觉比较像反证法，就是如果它的子问题都不是弧不一致的，那它就是SAC的）

SAC严格比maxRPC强。 在图3.6中给出了SAC修剪比maxRPC更多值的网络示例。 SAC的第一种算法由Debruyne和Bessierein [43]提出，并且被称为SAC1。 它是一种强力算法，通过在每个子问题N | xi = vi上执行AC来检查每个值的SAC。 如果N | xi = vi是弧不一致，则它从D（xi）中移除vi。 在域中每次更改后，它会重新检查每个剩余值的SAC。 然后它可以在每个子问题上执行AC nd次，并且因为存在nd子问题，所以它在二进制规范化网络上的O（en2d4）中运行，其中AC是O（ed2）的。在[6]中，Bart`ak和Erben提出了SAC2，这是一种更智能的算法，通过存储支持列表来避免不必要的工作，有点像AC4。 不幸的是，它的最坏情况时间复杂度仍然是O（en2d4）。 最近，Bessiere和Debruyne表明，二进制归一化网络上SAC的复杂性在O（end3），并且他们提出了SAC-Opt，一种具有这种最佳时间复杂度的算法[16,17]。为了实现最佳时间，SAC-Opt将大量信息存储在需要O（end2）空间的大型数据结构中。 SAC-SDS（共享数据结构）是一种较轻的版本，其中存储的结构较少。 其O（end4）时间复杂度是前SAC算法和SAC-Opt之间的折衷，而其空间复杂度与SAC2相同，即O（n2d2）。 Lecoutre和Cardon提出了SAC3，这是一种强制执行SAC的不同技术[82]。 SAC3递增地将值分配给网络中的变量，直到弧一致性消除域。如果当前的赋值顺序是I =（（x1，v1），...，（xk，vk）），则推断出值 (x1,v1),(x2,v2),...,(xk−1,vk−1)当前是SAC。 该技术允许在单个弧一致性通过中证明多个值的SAC。 SAC3没有最佳的最坏情况时间复杂度，但在实践中效果很好。

已经提出了SAC的若干扩展。 Prosseretal提出了受限制的SAC，这是一种弱化的SAC版本，可以在一次通过中检查每个值的SAC，而不会将删除传播到已经处理的值[102]。 在[12,34,16]中提出了一些比SACitself更强的细微扩展。 尚未评估有效性和实践效率。

可以构造许多其他单独一致性，因为可以使用任何局部一致性来检测网络N | xi = vi的可能的不一致性。 如果可以在多项式时间内强制执行局部一致性，则相应的单例一致性也具有多项式最坏情况时间复杂度。 Prosser等人分析了这一更广泛的图景。 在[102,122]中，他们理论上比较了（i，j） - 一致性和单一（i，j） - 一致性的修剪能力：

图3.7总结了本节中提出的局部一致性之间的定性比较。 完整的证明可以在[44]中找到。 Verfaillie等人提出了一种通用的算法模式，可以强制执行本节中提到的大多数局部一致性，以及现有的一致性[119]。