Removing Propagation Redundant Constraints in Redundant Modeling 翻译（一）

最新推荐文章于 2022-11-11 20:03:58 发布

达小七

最新推荐文章于 2022-11-11 20:03:58 发布

阅读量512

点赞数

分类专栏：学习

学习专栏收录该内容

55 篇文章 2 订阅

订阅专栏

消除冗余建模中的传播冗余约束

abstract

一种广泛采用的解决约束满足问题的方法是将系统树搜索和不同程度的约束传播相结合，对搜索空间进行剪枝。提高执行效率的一种常见技术是添加冗余约束，这些约束是问题模型中其他约束逻辑上隐含的约束。然而，一些冗余约束是传播冗余，因此不会向约束求解器提供额外的传播信息。冗余约束是在冗余建模过程中自然产生的，在冗余建模过程中，同一问题的两个模型通过通道约束进行连接和组合。本文给出了证明一个约束相对于信道约束和另一个模型中约束的传播冗余的一般定理。在CSPlib (http://www.csplib.org)的问题上，我们说明了如何在冗余建模中检测和删除传播冗余约束可以将搜索速度提高几个数量级。

附加关键词和短语:约束传播，冗余约束，冗余建模

1. INTRODUCTION

有限域约束编程将回溯树搜索与约束传播相结合，以解决约束满足问题（CSPs）[Mackworth 1977]。约束传播从变量域中删除不可行值以减少搜索空间。这种基于传播的约束求解框架在现代约束规划系统中实现，例如ECLiPSe [Cheadle等2003]，ILOG Solver [1999]和SICStus Prolog [2003]，它们已成功应用于许多实际工业应用。

通常有多种方法可以将问题建模为CSP。通过将问题建模为CSP，我们指的是确定变量，变量的关联域以及约束的表达式的过程。找到一个好的CSP模型是一项具有挑战性的任务。建模者必须指定一组捕获问题定义的约束，但这还不够。该模型还应具有强大的传播性：即，它应该能够快速减少问题变量的域。此外，执行约束传播的传播器的实现应该是有效的。最后但并非最不重要的是，变量和相关域的选择应该导致比其他域更小的搜索空间。

增加传播强度的常用技术是添加冗余约束（redundant constraints），这些约束在逻辑上由模型的约束暗示。 Carlier和Pinson [1989]出现了冗余约束的早期和重要用途，用于解决作业车间调度问题。添加冗余约束可能是有益的，因为约束求解器可以从这些冗余约束中提取更多信息。但是，某些逻辑冗余约束是传播冗余，因此不会向约束求解器提供额外的传播信息。通常，我们只想添加不是传播冗余的冗余约束以减少搜索空间。

此检查是多余的，因为此约束可以删除的任何内容都将被其他两个删除。这个约束是传播冗余（propagation redundant）。

显然，约束x1≥x3在逻辑上是由约束x1≥x2和x2≥x3暗示的。请注意，如果x1≥x3是检查的第一个约束，它确实会从x3的域中删除值2。但是，很容易验证通过从模型中删除x1≥x3，我们仍然可以获得完全相同的结果域。因此，x1≥x3不会（真正）为模型贡献额外的域减少。

请注意，逻辑冗余并不意味着传播冗余。

注意，相对于x1-x2≥0∧x1+x2≥0，x1≥0在逻辑上是冗余的。但显然它不是传播冗余。

根据检查约束的顺序，传播冗余约束可能或者不能从域中移除值（如前所述）。因此，肯定存在与传播冗余约束相关联的运行时成本。删除传播冗余约束会导致我们在约束传播后得到完全相同的域，但传播成本要低得多，我们将在后面的实验中看到。

冗余建模（redundant modeling）是逻辑冗余约束的一个重要来源[Cheng et al. 1999]。一个问题可以用两组不同的变量从两个不同的视点建模。通过将两种不同的模型与信道约束（channeling constraints）联系起来，将两种模型中的估值关联起来，可以使组合模型具有更强的传播行为。然而，额外的变量和约束增加了额外的计算开销。假设每个模型都是完整的，并且只允许保持满足问题的解，那么每个模型相对于另一个模型加上通道约束在逻辑上是冗余的。在许多情况下，与组合模型中的其他约束相比，其中一些约束也是传播冗余的。通过对传播冗余的推理，我们可以通过保持约束条件来改进冗余建模，从而实现有益的新传播。

在本文中，我们引入了限制和非限制信道函数的概念来描述信道约束。基于传播规则的概念，研究了约束的传播行为，该规则通过约束捕获每一种可能的传播。这允许我们通过简单的蕴涵测试系统地确定一个传播器相对于一组约束的传播器是否是冗余的。给出了证明冗余模型中约束传播冗余的一般定理。

我们关注执行(组合)两种流行传播技术的传播器，即域传播（domain propagation）[Van Hentenryck et al. 1998]和设置边界传播（set bounds propagation）[Gervet 1997]，包括实现这些方法的全局约束(参见示例26)。我们使用的底层机制可以表示任何只处理整数域和设置边界的传播器，我们的一些结果直接适用于此类传播器。尽管我们不认为更强的基于集合的传播器更能解释基数[Azevedo和Barahona 2000;，我们可以理解更强的基数推理作为附加约束使用隐式基数变量。因此，我们可以使用额外的传播器对公共基数推理建模。

我们在CSPLib（http://www.csplib.org/）的问题上说明了如何检测和消除传播冗余约束可以显着加快求解行为。本文是我们早期工作的修订版和扩展版[Choi et al。 2003a，2003b]。

本文的其余部分组织如下。在第2节中，我们介绍了基于传播的约束求解和传播规则，这是一种列举传播器不同传播行为的方法。在第3节中，我们给出了在确定传播冗余约束时有用的定理。在第4节中，我们定义了我们的方法所涵盖的通道约束的广泛形式。在第5节中，我们给出了一些定理，这些定理允许我们展示冗余模型中的哪些约束不会导致额外的传播，并且可以删除。在第6节中，我们给出了实验结果，表明了检测和消除传播冗余约束的好处。在第7节，我们将讨论相关工作。在第8部分，我们总结了我们的贡献，并阐明了未来的研究方向。

2. BACKGROUND

在第2节中，我们介绍了基于传播的约束求解和传播规则，这是一种列举传播器不同传播行为的方法。

在本文中，我们考虑使用约束传播和树搜索求解整数和集约束。在滥用符号时，我们将布尔变量的算术约束称为布尔约束，它们通常称为伪布尔约束。因此，布尔约束求解被认为是整数约束求解的特例。我们的符号虽然与传统的CSP文献不同，但我们可以用更简单的方式表达理论框架。

2.1 Variables and Domains 变量和域

我们考虑一组变量V =VI∪VV由整数变量VI（使用小写字母如x和y），和整数变量的集合VS（使用大写字母如 S和T）组成。我们用v来表示任何一种变量。每个变量都与一组有限的可能值相关联，这些值由CSP的域定义。域D是从固定（可数）变量集V到有限整数集（对于VI中的整数变量）和有限整数集（对于VS中的集变量）的有限集的完整映射。一个false domain D是指对于某些具有D（v）=∅的域的v。单域（singleton domain）D是指对于所有有|D(v)| = 1。两个域的交集（intersection of two domains）意味着。D1 is stronger than D2，记作如果对所有v，有。D1 is equal to D2，（也是对所有v）。我们将对初始域的概念感兴趣，我们将其表示为Dinit。初始域为每个变量提供了可能的初始值。实际上，初始域允许我们限制对域D的注意，使得。我们也尽可能使用范围表示法：l和u是整数，[l..u]表示集合{d | l ≤ d ≤ u}；L和U是整数集合，[L..U]表示整数集合的集合{A | L ⊆ A ⊆ U}。

2.2 Valuations, Infima and Suprema 估值、下确界和上确界

估值θ是整数变量（xi∈VI）到整数值的映射，并且将变量（Si∈VS）设置为整数值集，写作

其中

让vars成为返回表达式，约束或估值中出现的变量集的函数。给定表达式e，通过用θ（v）替换每个v∈vars（e）并计算得到的变量自由表达式的值来获得θ（e）。在滥用符号时，我们将估值θ定义为域D的元素，记作如果对于所有，有。将估值θ投影到变量V上，表示为，即估值

将关于域D的表达式e的下限和上限定义为.。inf和sup使用的排序取决于表达式的类型。如果e具有整数类型，则，而如果e具有整数集合类型，则。请注意，对于任意域和整数类型表达式集，这些值可能不存在。稍后我们将自己局限于域和表达式，其中infimum和supremum总是存在。

2.3 Constraints and CSPs

约束对一组变量的允许值进行限制，通常用很好理解的数学语法编写。更正式地，约束c是使用特定约束语言中的可用函数和关系符号表达的关系。为了本文的目的，我们假设算术约束的通常（整数）解释，设置诸如ε和operators的运算符，以及诸如¬，∧，∨，⇒和⇔的逻辑运算符。我们定义这是使约束c成立的θ的集合。我们称solns（c）为c的解。在某些情况下，也可以通过给出集合（或表）solns（c）直接定义约束。我们有时将整数约束c视为表达式，如果为true则值为1，如果为false则为0。我们可以以明显的方式将域D理解为约束，

CSP由一组作为连词读取的约束组成。 CSP的解决方案是使得CSP的每个约束成立的估值，即对于CSP的所有约束c，有 ∈ solns(c)。如果则约束c和c'在逻辑上是冗余的。向CSP添加逻辑冗余约束不会改变CSP的解决方案。

2.4 Propagators and Propagation Solvers

在基于传播的约束求解上下文中，约束指定了一个传播器，它给出了传播的基本单元。传播器f是从一个域到另一个域的单调递减函数；也就是说，，意味着。一个传播器f对于约束c是正确的，如果对于所有域D都满足

这是一个弱限制，因为，例如，身份传播器（identity propagator）对于所有约束c都是正确的。我们假设约束c的传播器f正在检查，即，如果D是单个域，如果存在θ∈D且θ∈solns（c），则f（D）= D。检查传播器正确地确定单个域的约束c的可满足性。

用于一组传播器F和当前域D的传播解算器（propagation solver），solv（F，D），从域D开始重复应用F中的所有传播器，直到得到的域没有进一步的变化。 solv（F，D）是最大的域，它是所有f ∈ F的固定点（即）。换句话说，solv（F，D）返回以下定义的新域

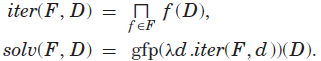
其中gfp表示the greatest fixpoint。

2.5 Domain and Set Bounds Propagators

传播器通常(但并不总是)与实现某种局部一致性概念相关联。一致性概念研究得最多的是arc consistency [Mackworth 1977]，它确保对于每个二进制约束，第一个变量域中的每个值，在满足约束的第二个变量域中都有一个支持值。弧一致性可以自然地扩展到两个以上变量的约束条件。这种扩展被称为广义弧一致性（generalized arc consistency）[Mohr和Masini 1988]，以及域一致性（domain consistency）[Van Hentenryck et al. 1998](这是我们将使用的术语)和超弧一致性（hyper-arc consistency）[Marriott和Stuckey 1998]。

域D对于约束c是域一致的（domain consistent），如果D是包含c的所有解θ∈D的最小域，即，不存在使得

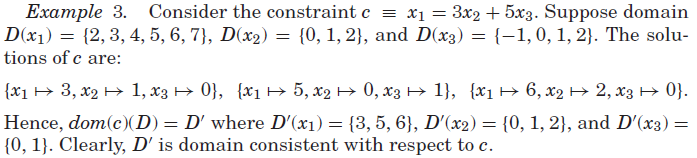
Set bounds propagation集合边界传播器[Gervet 1997]通常用于域将集合变量映射到整数的下界集和整数的上界集。我们将通过将注意力限制在D（S）是范围的域，即来强制执行此操作。这是通过仅使用set bounds传播器来达到的，它们维护此属性。 set bounds传播器返回最小的设置范围，其中包括域传播器返回的结果。

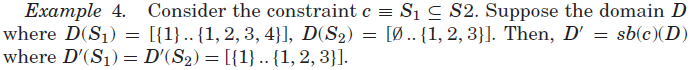
约束可以同时包含整数和集合变量。在这种情况下，我们对整数变量使用域传播，对集合变量使用边界传播。

2.6 Atomic Constraints and Propagation Rules

原子约束表示在传播期间发生的域中的基本更改。对于整数变量，原子约束表示从整数域中消除值，即xi $\neq$ d或xi = d其中xi∈ $\nu _{I}$ 且d是整数。对于集合变量，原子约束表示向下限整数集合添加值或从整数上限集合中删除值，即d∈Si或d $\notin$ Si，其中d是整数且Si∈ $\nu _{S}$ 。

为了便于标记，我们将编写扩展规则，其中C' 是原子约束的组合，作为一组规则的缩写。传播规则以一种明显的方式定义了一个传播器(我们对其使用相同的表示法)。

换句话说，定义了一个传播器，它仅在D暗示C时才基于c从D中移除值。我们可以根据它实现的传播规则来表征任意传播器f。

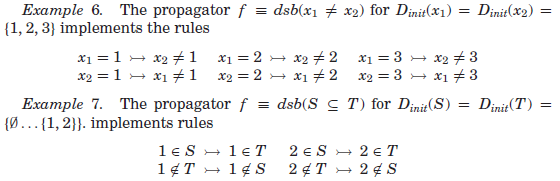
设 $\phi _{f}$ 是实现 f 的所有可能规则的集合。 f 的这个定义通常是不合理的。为了更有效地推断给定传播器的传播规则，我们需要具有最小的表示。

也就是说，由 f 引起的所有传播也是由 $\Pi _{f}$ 引起的。请注意， $\Pi _{f}$ 不是唯一的。

注意，布尔域{0,1}的约束的传播规则可以仅使用包括方程的原子约束来表示，因为对于b $\in$ {0,1}，有

3. PROPAGATION REDUNDANT CONSTRAINTS

在第3节中，我们给出了在确定传播冗余约束时有用的定理。

我们将研究关于传播器集冗余的推理。我们说一组传播器F1比一组传播器F2更强，记作F1>>F2，如果对于所有域D $\sqsubseteq$ $D_{init}$ 有。我们说一组传播器F1等价于一组传播器F2，记作F1 $\approx$ F2，如果对于所有域D $\sqsubseteq$ $D_{init}$ ，有。如果F >> {f}，传播器f由一组传播器F进行传播冗余。我们的主要目标是发现并消除传播冗余约束和/或传播器。在我们确定传播冗余约束之前，我们需要建立一些定理。

以下引理揭示如何用传播规则表示传播器。由约束c的dsb（c）实现的传播规则正好是那些，其中c表示。

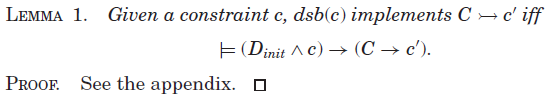
引理1使我们能够将约束的逻辑冗余与传播器的传播冗余关联起来。一个约束c2相对于约束c1在逻辑上是冗余的，它也相对于c1传播冗余。

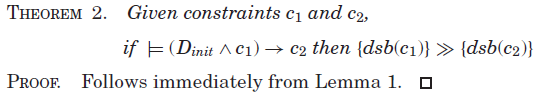
通常，逻辑冗余约束通过与其他约束的结合而在逻辑上成为冗余约束。然而，众所周知，在一般情况下，约束联合的域(和集边界)传播并不等价于单独应用域(和集边界)传播器。

如果约束c对于约束c1和c2的并集在逻辑上是冗余的，那么根据定理2（Theorem 2），{dsb(c)}对于{dsb(c1∧c2)}是传播冗余。然而，约束编程系统通常为每个约束实现一个单独的传播器。根据引理3（Theorem 3），{dsb(c)}对于单个约束集合的传播器(即{dsb(c1)， dsb(c2))来说，不一定是冗余的传播。因此，(通常)很难确定逻辑上冗余的约束相对于约束的并集而言是否是传播冗余。有趣的是，在一种情况下，约束的并集的传播等价于在各个合取上的传播。

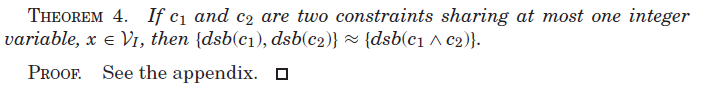
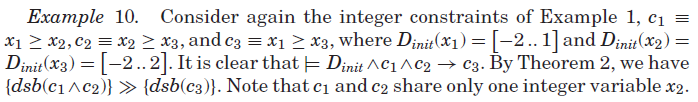
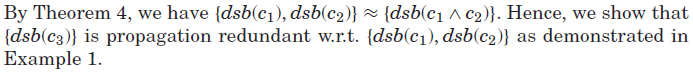
注意，在例2中，约束共享的变量不止一个，因此因此，虽然对于是逻辑冗余的，但它不是传播冗余的。

注意，当共享的单个变量是一个集合变量时，定理4并不成立，因为我们只应用集合边界传播器（set bounds propagation）。如果我们确实使用了set domain propagators，那么结果很容易扩展到单个共享变量是集合变量的情况。

但是，如果我们使用集合域传播器（set domain propagators），则，其中，。因此，当共享变量是一个集合变量并且我们使用set domain propagators时，定理4成立。

4. CHANNELING CONSTRAINTS

在第4节中，我们定义了我们的方法所涵盖的通道约束的广泛形式。

冗余建模[Cheng et al 1999]从多个角度对问题进行建模。通过使用通道约束连接两个模型，我们可以获得两种传播源的优势。

假设我们有一个问题模型 $M_{X}$ 使用变量X，另一个模型 $M_{Y}$ 使用不相交变量Y。通道约束可以用来通过关联X和Y将这两个模型连接在一起。究竟是什么渠道约束，目前还没有真正的一致意见。出于我们定理的目的，我们定义了一个通道约束，如下所示。

设 $A_{X}$ 是变量X上Dinit的原子约束， $A_{Y}$ 是变量Y上Dinit的原子约束。通道函数♦是从原子约束 $A_{X}$ 到 $A_{Y}$ 的双射。我们将通道函数扩展为以明显的方式映射原子约束的并集，其中c1,...,cn是原子约束。

注意，对于通道函数，根据定义，也是通道函数，是相同的。我们现在说明公共渠道如何适应这个框架。

4.1 Permutation Channels 排列通道

冗余建模的一种常见形式是当我们考虑两个观点来解释排列问题时[Geelen 1992]。在排列问题中，目标是在满足所有其他问题特定约束的两组对象 A = {a1, . . . , an} 和 B = {b1, . . . , bn} 之间找到二分匹配。通常，我们可以从两个不同的角度对排列问题进行建模。在第一个视点中，我们将对象从B分配给A。我们使用变量集 X = {x1, . . . , xn} 来表示A中的对象，用域1≤i≤n，来表示B中的对象。第二个视点，交换A和B之间的角色，即从A分配对象。我们使用变量集 Y = {y1, . . . , yn} 表示B中的对象，域，1≤j≤n 表示A中的对象。

对于所有1≤i，j≤n，排列通道函数被定义为和。排列通道等同于约束的并集

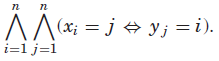
Example 12. Langford’s Problem CSPLib中的“prob024”问题就是排列问题的一个例子。问题是找到一个(m×n)位序列，该序列包含数字1到n，每个数字出现m次。在数字1的任何连续对之间有一个数字，在数字2的任何连续对之间有两个数字，…，以及任意一对数字之间的n位。

Smith [2000]提出了两种模拟Langford问题的方法。我们使用（3×9）实例来说明这两个模型。在第一个模型 $M_{X}$ 中，我们使用27个变量，我们可以将其视为这里， $1_{1}$ 表示序列中的第一个数字1， $1_{2}$ 表示第二个数字1，依此类推。这些变量的初始域，，表示序列中数字xi的位置。我们将Smith模型的约束条件列举如下：

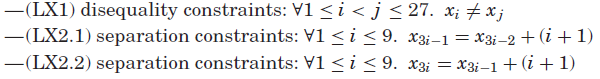
在第二个模型 $M_{Y}$ 中，我们同样使用27个变量表示序列中的每个位置。这些变量的初始域，对应于序列的位置yi中的数字。这些约束是：

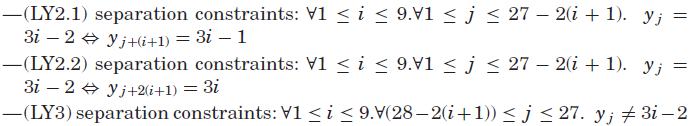
对于所有1≤i，j≤27，两个模型的排列通道是，对于所有。

Example 13. All Interval Series Problem CSPLib中的“prob007”问题来自于音乐作曲。问题是找到n个数从1到n的排列，使相邻数之间的差形成从1到n - 1的排列。我们给出了两种建模方法。第一个模型来源于Puget和R’egin[2001]提出的模型，第二个模型对Choi和Lee[2002]提出的模型进行了轻微的修改。

第一个模型 $M_{X}$ 由n个变量组成。每个xi表示位置i的数字和。我们引入辅助变量来表示相邻数字之间的差异，其中。约束是：

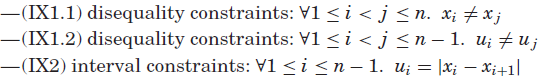
第一个模型 $M_{Y}$ 同样由n个变量组成。每个yi表示位置i的数字和。辅助变量表示1到n-1的差值所属的位置，且。约束是：

(IY2.1)和(IY2.2)约束规定，如果yi和yj相邻，它们之间的差的位置必须是它们中较小的一个。在第二种模型中，只有数字1和n可以给出n - 1的差。因此，我们可以添加以下冗余约束:，这要求y1和yn相邻。

这个问题的排列通道更有趣，因为我们在每个模型中有两种不同的变量，每个变量都由一个排列通道相关联。通道是和。

4.2 Boolean Channels 布尔通道

另一种常见的冗余建模形式是我们同时给出整数和布尔模型。假设我们有一个整数模型，使用整数变量 X = {x1, . . . , xn} 和域Dinit（xi）= [1 .. k]。我们可以使用布尔变量得到相应的布尔模型。每个变量编码的命题。布尔通道函数 $\Delta$ 被定义为和，对于所有1≤x≤1n，1≤x≤k。请注意，布尔变量不需要原子约束，因为它们等效（分别）为。布尔通道 $C_{\Delta }$ 等效于约束的并集

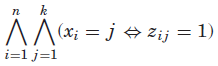
Example 14. n-Queens Problem 这个众所周知的问题是将n个皇后放在n×n棋盘上，这样就不会有两个皇后可以相互攻击。有两种常见的方法来模拟这个问题，即整数模型和布尔模型。

整数模型 $M_{X}$ 由n个变量组成，每个xi表示第i行皇后的列位置，，1≤i≤n，约束条件为：

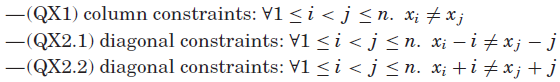
布尔模型 $M_{Z}$ 由n×n个布尔变量组成。每个布尔变量 $z_{i,j}$ 表示我们是否在第i行第j列有一个女王。约束是：

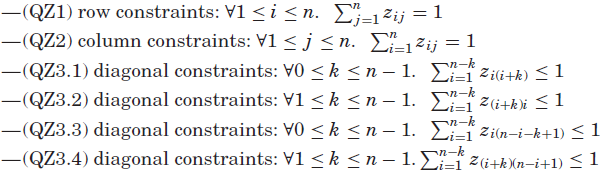
我们使用布尔通道结合这两个模型，。

4.3 Set Channels

冗余建模的另一种常见形式是一个模型处理整数变量，另一个模型处理有限整数集上的变量，当且仅当i∈Sj，则关系xi = j成立。这将排列问题推广到两个或多个整数变量可以取相同值的位置。假设整数变量是，其中，而集合变量是，其中，。

集合通道函数（set channel function）{}被定义为和，。集合通道 $C_{\left \{ \right \}}$ 等价于

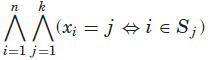
Example 15. Social Golfers Problem CSPLib中的“prob010”问题是将n = g×s的玩家安排到g个组中，每个组有s个玩家，连续玩w周，这样就不会有两名玩家在同一组中玩两次。Smith[2001]提出了两种方法来建模这个问题。

在第一个模型中，我们使用变量来表示玩家l在第k周所在的组，和，。

问题的约束可以表示为：

第二模型使用集合变量来表示在第k周的组i中玩的一组玩家。和，。约束表达为：

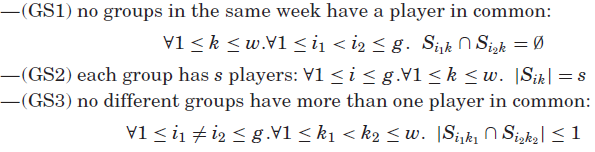
我们可以通过集合通道来结合两个模型，，。

Example 16. Balanced Academic Curriculum Problem 在CSPLib中列为“prob030”的问题是设计一个学术课程，旨在平衡每个学术时期的负荷。按照Hnich等人[2002]中的描述，我们可以得到整数模型 $M_{X}$ 和集合模型 $M_{S}$ 。

给定m个课程和n个时期，a，b是每个时期允许的最小和最大学术负荷，c，d是每个时期允许的最小和最大课程数，ti指定课程i的学分数，R是一组先决条件对<i，j>，指定必须在课程j之前进行课程。

我们引入了一组辅助变量 $l_{j}$ ，它们由两个模型共享，表示期间j中的学术负荷，以及表示任何时期中最大学术负荷的变量u，。目标函数是最小化u。我们还引入了另一组共享辅助变量 $q_{j}$ 来表示分配给一个时期的课程数量。我们有。

我们有以下两种模型共有的约束：

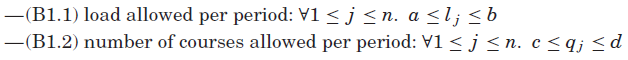
我们还添加了以下冗余约束：

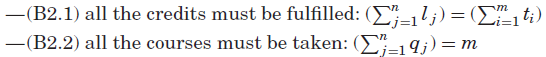
在整数模型 $M_{X}$ 中，变量表示指定课程i的时间段，，整数模型 $M_{X}$ 的约束条件为：

在集合模型中，集合变量表示分配给期间j的课程集合，。集合模型 $M_{S}$ 的约束是：

我们可以用集合通道来结合两个模型，，。

4.4 Channels between Set and Boolean Models

冗余建模的一种非常少见的形式是，我们给出一个集合模型和这个模型的布尔版本。不常见的原因是，在向布尔模型转移的过程中，没有自然的表达增益。

假设集合变量是布尔变量是。集合到布尔变量的通道函数（set2bool channel function）被定义为。set2bool channel function等价于

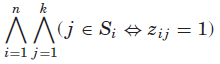
通过通道，我们可以将公共集约束（c）映射到布尔约束，如图1所示。我们将证明集约束（c）的集合边界传播等效于相应布尔约束的域传播。

5. PROPAGATION REDUNDANT CONSTRAINTS IN REDUNDANT MODELING

在第5节中，我们给出了一些定理，这些定理允许我们展示冗余模型中的哪些约束不会导致额外的传播，并且可以删除。

在冗余建模中，每个模型相对于另一个模型加上通道约束在逻辑上是冗余的。通常，为两个视点定义的传播器以不同的方式工作，并在搜索的不同阶段发现信息。然而，我们展示了两种可能性，其中由一些模型中的某些约束引起的传播可以通过以下方式变得冗余：（a）通过信道从另一模型中的约束引起的传播和（b）信道本身的传播。为了简洁起见，我们在陈述一些引理和定理时将集中于一个模型。通过研究逆通道函数，另一种模型的局限性也可以容易看出。

5.1 Propagation Redundancy through Channels

为了证明一个模型中某些约束引起的传播是由另一个模型中约束通过信道引起的传播所包含的，我们通常需要将传播器的考虑分解为单个的传播规则。因此，我们需要以下引理来确保约束的域和集合边界传播器等价于由传播器实现的传播规则的并集。

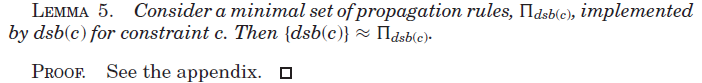
接下来，我们需要正式定义包含（subsumption）的概念。

（定义一条传播规则包含另一条传播规则）

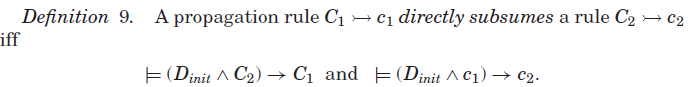
通道函数使我们能够将传播规则r从一个模型映射到另一个模型。如果映射的传播规则直接包含在另一个模型中的另一个传播规则r'中，那么下面的引理告诉我们，r对于信道传播器和r'是冗余的传播。

我们可以直接把引理6的结果提出来，讨论约束条件下域和集合边界传播器直接包含的传播规则。

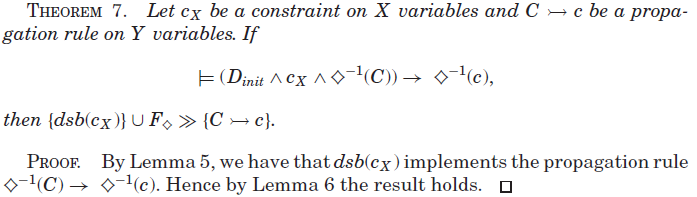
定理7的推论是，如果dsb（ $c_{Y}$ ）实现的最小传播规则集中的每个传播规则都由dsb（ $c_{X}$ ）通过信道函数包含，那么dsb（ $c_{Y}$ ）相对于信道传播器和dsb（ $c_{X}$ ）是传播冗余的。

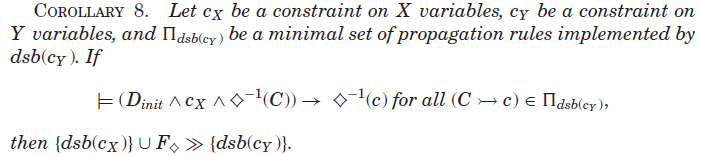
其中。类似的参数适用于其他传播规则（r2），（r3）和（r4）。因此，使用推论8，dsb（ $c_{Y}$ ）相对于和dsb（ $c_{X}$ ）是传播冗余。

对于（LY2.2）约束，，其中且，我们可以类似地表明相对于传播冗余，其中（LX2.2）。虽然模型 $M_{X}$ 不包括传播器，但我们仍然可以通过定理4发现它是传播冗余，因为。

类似的推理对（LY3）的约束同样适用，其中该约束相对于是传播冗余。

为简洁起见，我们将引入伪原子约束x≤d等效于的并集，和x≥d等效于的并集，以讨论下一个例子。

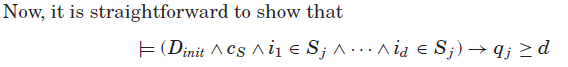
其中。类似的推理同样适用于其他传播规则（r2）,（r3），（r4）。因此，根据推论8，相对于传播冗余。

类似的推理可以运用到约束（BX1），，。相对于和是传播冗余的，其中（BS2）中的。

通常，单个约束不会捕获约束对置换模型另一侧的所有传播效应。在这种情况下，我们可能需要为每个特定的传播规则找到导致相同传播发生的另一侧的约束。

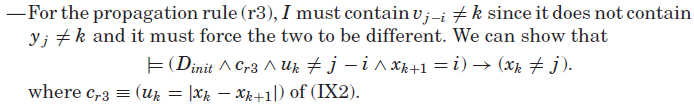
注意，即使每个示例传播规则（r1）到（r3）由和（IX2）的传播冗余，我们确实需要对k的每个不同值使用不同的约束。

类似的推理可以运用到其他（IY2.2）的约束，相对于传播冗余。

注意，逻辑冗余的（IY3）约束并不是传播冗余的。

5.2 Propagation Redundancy Caused by Channels

通道本身实际上可能限制所涉及的一个或两个模型中的可能解决方案。

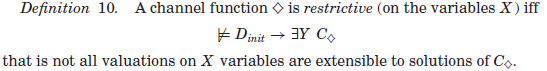
并非所有X变量的赋值都可以扩展到C♦的解。

5.2.1 Restrictive Channel Functions.

限制性信道函数本身可以使约束传播冗余。Smith[2000]首先观察到置换通道使得两个模型传播中的变量间的每一个不等式都是冗余的。Walsh[2001]证明了这适用于其他一致性的概念。

布尔通道中隐含的是每个整数变量只能占用一个，并且必须取一个值。这在布尔模型中表示为约束。它由限制性通道函数强制执行。

通道函数 $\left \{ \right \}^{-1}$ 是限制性的，因为每个变量xi∈X只能取一个值j。这意味着，。很明显， $F_{\left \{ \right \}}$ 使这些约束传播变得多余。

5.2.2 Unrestrictive Channel Functions.

非限制性通道函数不使(对X)传播的任何约束成为多余的。有趣的是，在这种情况下，我们可以简单地根据逻辑结果来讨论传播冗余。如果一个约束 $C_{X}$ 通过一个非约束通道逻辑上暗示另一个约束 $C_{Y}$ ，则dsb( $C_{X}$ )包含由dsb( $C_{Y}$ )实现的所有传播规则。

我们可以直接利用引理13的结果，通过非约束信道，简单地根据逻辑蕴涵确定约束的传播冗余。

要使这个结果成立，通道函数必须是无约束的，原因是在一般情况下太弱。

我们可以使用定理14来证明我们的例子中许多传播器的传播冗余。

下面的示例说明，我们的方法也适用于全局约束的传播器。在n-Queens问题中使用alldifferent全局约束会使约束(QZ2)传播变得冗余。

在一定程度上，由于通道在两个方向上都是无约束的，我们可以证明集合边界传播器（set bounds propagation）提供与集合约束到布尔值的映射相同的传播强度。

为便于参考，表I总结了本节中提供的结果。这可以作为问题建模者的指南，以快速识别哪些定理与他们的问题相关。

达小七

关注

0
点赞
踩
0

收藏

觉得还不错? 一键收藏
0
评论
Removing Propagation Redundant Constraints in Redundant Modeling 翻译（一）

消除冗余建模中的传播冗余约束abstract一种广泛采用的解决约束满足问题的方法是将系统树搜索和不同程度的约束传播相结合，对搜索空间进行剪枝。提高执行效率的一种常见技术是添加冗余约束，这些约束是问题模型中其他约束逻辑上隐含的约束。然而，一些冗余约束是传播冗余，因此不会向约束求解器提供额外的传播信息。冗余约束是在冗余建模过程中自然产生的，在冗余建模过程中，同一问题的两个模型通过通道约束进行连...
复制链接

扫一扫