css贝塞尔曲线 多个点_了解贝塞尔曲线的数学和Python实现示例

贝塞尔曲线在计算机图形学中被大量使用，通常可以产生平滑的曲线。如果您曾经使用过Photoshop，则可能会发现名为“锚点”的工具，您可以在其中放置锚点并用它们绘制一些曲线，这些也是贝塞尔曲线。如果您使用了基于矢量的图形SVG，这些也会使用贝塞尔曲线。让我们看看它是如何工作的。

定义

给定n + 1 个点(P0，…，Pn)称为控制点，这些点定义的贝塞尔曲线定义为：

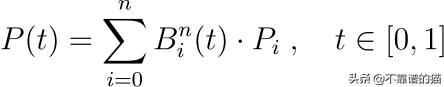
eq. 1

其中B(t)称为Bernstein多项式：

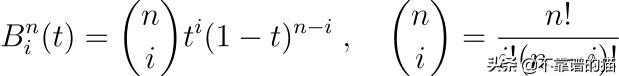
eq. 2

你会注意到这个伯恩斯坦多项式看起来很像牛顿二项式公式中的第k项，也就是:

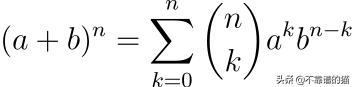
eq. 3

事实上，伯恩斯坦多项式就是(t + (1 - t))^n = 1的展开式中的第k项。这就是为什么如果你把所有的Bi加到n，你会得到1。

二次贝塞尔曲线

二次贝塞尔曲线就是我们所说的有三个控制点的贝塞尔曲线，P(t)的阶数是2。让我们计算给定3个控制点的贝塞尔曲线，并探索一些我们可能会发现的特性！请记住，公式1适用于n+1个点，所以在我们的例子中n=2。

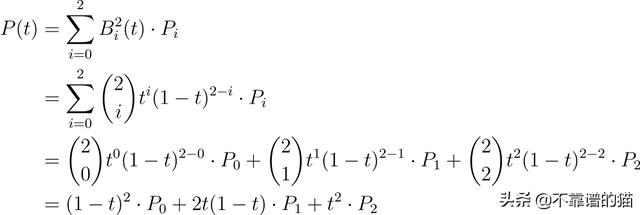
eq. 4

注意，P(t)返回的不是一个数字，而是曲线上的一个点。现在我们只需要选择三个控制点，然后在[0,1]范围内对曲线求值。我们可以在Python中很容易地做到这一点。

import numpy as npimport matplotlib.pyplot as pltP0, P1, P2 = np.array([[0, 0],[2, 4],[5, 3]])# define bezier curveP = lambda t: (1 - t)**2 * P0 + 2 * t * (1 - t) * P1 + t**2 * P2# evaluate the curve on [0, 1] sliced in 50 pointspoints = np.array([P(t) for t in np.linspace(0, 1, 50)])# get x and y coordinates of points separatelyx, y = points[:,0], points[:,1]# plotplt.plot(x, y, 'b-')plt.plot(*P0, 'r.')plt.plot(*P1, 'r.')plt.plot(*P2, 'r.')plt.show()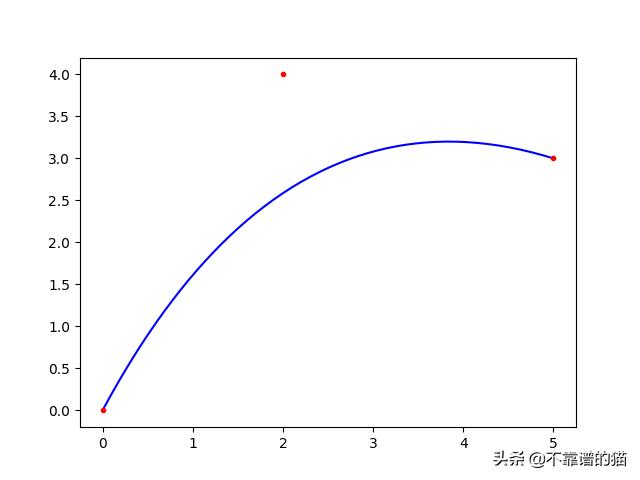

您会注意到曲线从第一个控制点处开始，到最后一个控制点处结束。这个结果对任意数量的点都成立。由于t的取值范围是从0到1，我们可以通过求P(t)在t=0和t=1时的值来证明这一点。使用eq.1:

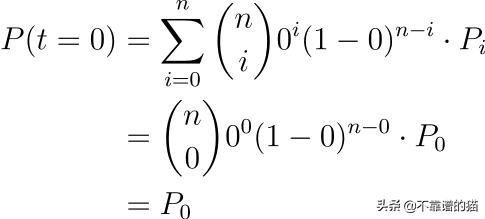
eq. 5

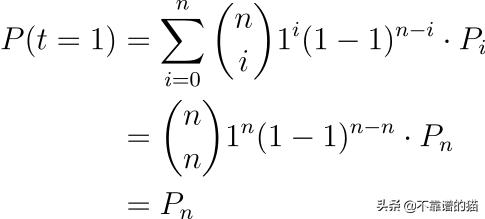
eq. 6

因为是从P0到P2，P1完全决定了曲线的形状。移动P1你可能会注意到:

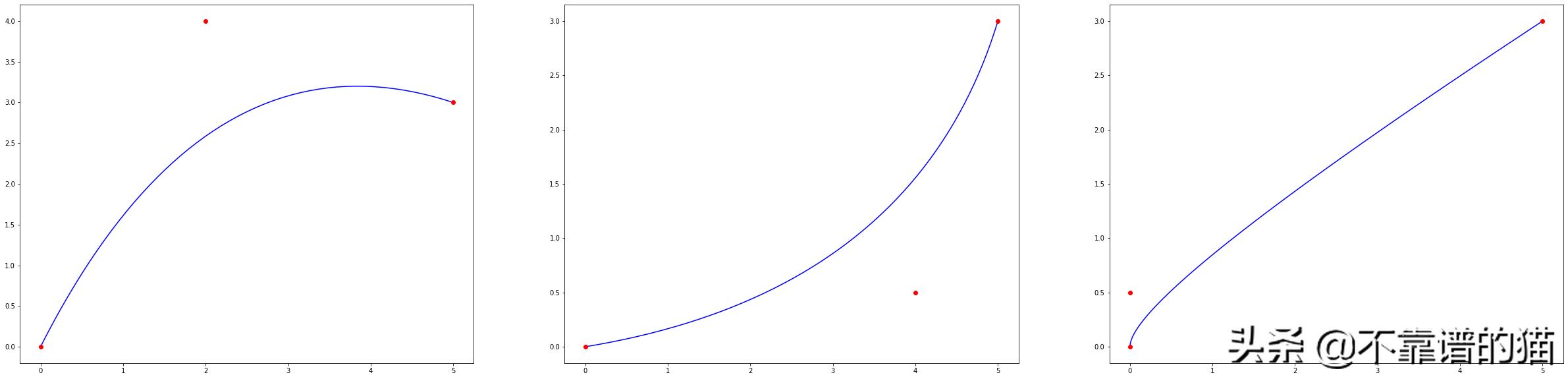
贝塞尔曲线总是包含在控制点形成的多边形中。这个多边形因此被称为控制多边形，或者贝塞尔多边形。这个属性也适用于任意数量的控制点，这使得它们在使用软件时的操作非常直观。

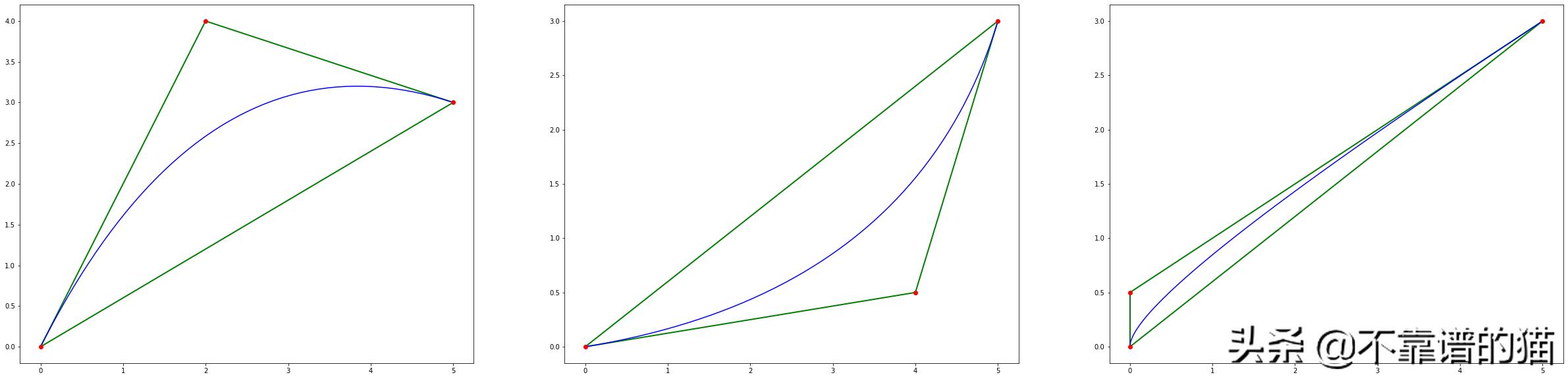
控制多边形还具有以下特性：包含曲线的面积最小，称为凸包。

插补

贝塞尔曲线的一个有趣应用是绘制一条通过一组预定义点的平滑曲线。之所以有趣，是因为P(t)的公式产生点，并且不是y = f(x)的形式，因此一个x可以具有多个y。。例如，我们可以这样画:

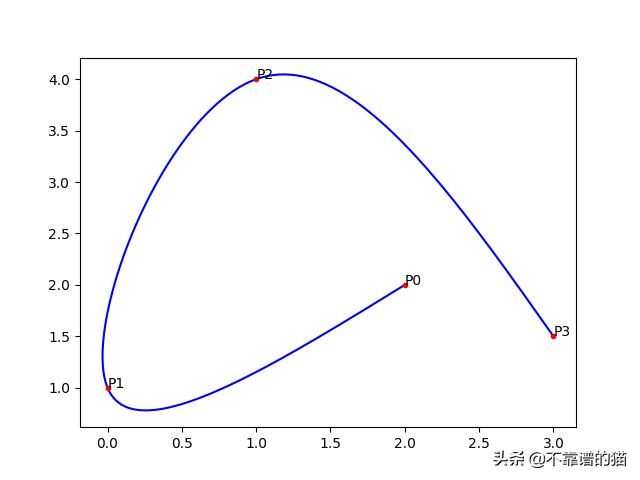
下面是如何使用公式1为任意数量的控制点编写通用版本的Bezier曲线。

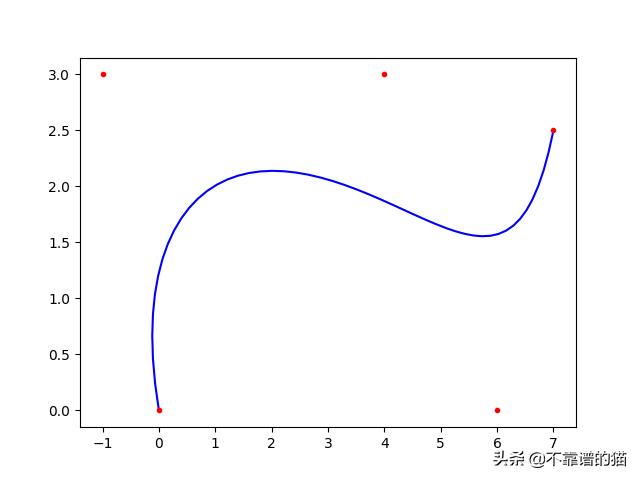
import numpy as npimport matplotlib.pyplot as pltfrom math import factorialdef comb(n, k):    return factorial(n) // (factorial(k) * factorial(n - k))def get_bezier_curve(points):    n = len(points) - 1    return lambda t: sum(        comb(n, i) * t**i * (1 - t)**(n - i) * points[i]        for i in range(n + 1)    )def evaluate_bezier(points, total):    bezier = get_bezier_curve(points)    new_points = np.array([bezier(t) for t in np.linspace(0, 1, total)])    return new_points[:,0], new_points[:,1]points = np.array([    [0, 0],    [-1, 3],    [4, 3],    [6, 0],    [7, 2.5]])x, y = points[:,0], points[:,1]bx, by = evaluate_bezier(points, 50)plt.plot(bx, by, 'b-')plt.plot(x, y, 'r.')plt.show()

运行该Python程序，显示如下图形：