每隔10秒执行一次_二元一次方程组行程问题，相遇追及、环形跑道、顺流逆流，你会吗...

行程问题是二元一次方程组中比较重要的一类问题，相遇问题、追及问题、环形跑道问题、顺流逆流问题、顺风逆风问题、火车过桥问题等等，这些问题你都会吗？

行程问题

例题1：某站有甲、乙两辆汽车，若甲车先出发1ｈ后乙车出发，则乙车出发后5ｈ追上甲车；若甲车先开出30ｋｍ后乙车出发，则乙车出发4ｈ后乙车所走的路程比甲车所走路程多10ｋｍ，求两车速度。

分析：利用甲车先出发1h后乙车出发，则乙车出发后5h追上甲车和甲车先开出20km后乙车出发，乙车出发4h后追上甲车，结合两车行驶的路程相等得出等式求出即可．

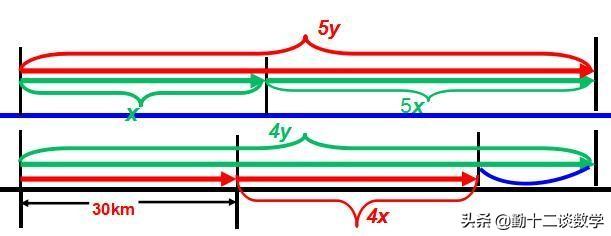
相遇追及问题

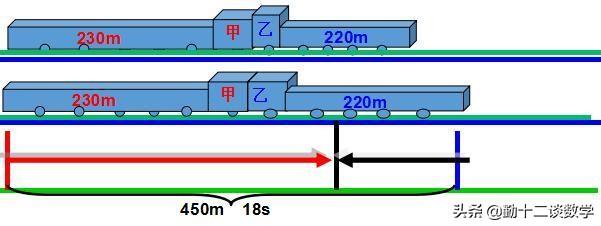
例题2：一列快车长230米，一列慢车长220米，若两车同向而行，快车从追上慢车时开始到离开慢车，需90秒钟；若两车相向而行，快车从与慢车相遇时到离开慢车，只需18秒钟，问快车和慢车的速度各是多少？

分析：由于两车两车相向而行，从相遇到离开所行的距离为两车的长度和230+220=450米，用时90秒，则速度和×相遇时间=总路程；如果同向而行，从快车追用慢车到离开的追及距离同为两车的长度为450米，用时18秒，则速度差×相遇时间=总路程．

环形跑道问题

例题3：甲、乙两人在周长为400ｍ的环形跑道上练跑，如果相向出发，每隔2.5min相遇一次；如果同向出发，每隔10min相遇一次，假定两人速度不变，且甲快乙慢，求甲、乙两人的速度．

分析：相向而行是相遇问题，要用到：甲路程+乙路程=两人相距路程；同向而行是追及问题，要用到：乙路程-甲路程=两人相距路程．

火车过桥问题

例题4：某铁路桥长1000m，现有一列火车从桥上通过，测得该火车从开始上桥到完全过桥共用了1min，整列火车完全在桥上的时间共40s．求火车的速度和长度．

分析：根据题中的火车完全通过桥，实际告诉我们火车所行路程为桥长+火车长；整列火车在桥上实际告诉我们火车所行路程为桥长-火车长，找到等量关系式：①火车行驶速度×时间1分钟=桥长+火车长；②火车行驶速度×40秒=桥长-火车长．

顺流逆流问题

船在顺水中的速度=船在静水中的速度+水流的速度

船在逆水中的速度=船在静水中的速度-水流的速度

例题5：已知A、B两码头之间的距离为240km,一艏船航行于A、B两码头之间,顺流航行需4小时 ;逆流航行时需6小时, 求船在静水中的速度及水流的速度.

分析：设船在静水中的速度为x千米/时，水流的速度为y千米/时，则顺水速度为(x+y)千米/时，逆水速度为(x-y)千米/时，根据往返路程相等建立等量关系求出其解就可以求出结论．

这几类问题，你会了吗？