本文深入探讨了群论在魔方旋转问题中的应用，特别是子群概念和生成元的作用。通过降群法减少魔方状态，利用群的性质简化解魔过程。文章介绍了群的阶、Lagrange定理、生成元和Cayley图，并讨论了不同生成元对群结构的影响。最后，阐述了如何通过改变生成元来解魔方，包括Thistlethwaite方法和Kociemba算法。
我会在本篇文章中着重介绍一些群论相关的知识，包括子群，生成元以及一些群的定理。最后介绍降群法解魔方。
前两篇文章：
法会因由：魔方与群论（一）(不要被标题吓到，高中生就可以看）zhuanlan.zhihu.com
Ideal Toy Company stated on the package of the original Rubik cube that there were more than three billion possible states the cube could attain. It's analogous to Mac Donald's proudly announcing that they've sold more than 120 hamburgers.
(J. A. Paulos, Innumeracy)
八、子群
上一篇文章我们介绍了，魔方群其实是置换群
显然，子群中必然包含单位元。那么我们以置换群为例。之前的文章中，我们介绍了，一个置换群中的置换分为奇置换与偶置换，那么猜一猜，一个置换群能否由奇置换或者偶置换构成子群呢？很显然，由于偶置换中包括单位元（恒等置换），而奇置换不包含，同时偶置换的复合一定是偶置换，因此所有的偶置换是置换群的一个子群，而奇置换不是。我们把置换群
除了偶置换构成的子群以外，置换群还有其他非平凡子群吗？
考虑置换群
同理，我们将所有保持2不动的置换拿出来，这些置换也构成子群：
如果我们取子群H和K的交集，我们发现他们的交集也是一个子群：
这就引出了子群的一个性质：两个子群的交集必然也是一个子群。请读者证明。
子群的第二个性质跟群元素的个数有关。我们将群元素的个数称为一个群的阶（order）。（注意，本系列文章中出现了多个“阶”，请大家分清他们的含义）显然只有有限群有阶。
Lagrange's theorem ：对于一个有限群G来说，其子群H的阶数必定能整除群G的阶数。
这个定理的证明我替大家完成，就不留作习题了（笑
我们设群G的阶数为n，群H的阶数为m，且m＜n，则群H可以写成：
我们取一元素
我们可以得到几个结论：
-
不构成群。（请读者说明理由）
-
中没有重复的元素。（
）
-
（
）
接下去，我们可以拿另一个H与
我们可以重复这个步骤，直到取不出以上所有集合之外的新的元素为止。假设我们取了k-1个g，则我们创造了k个集合：
这个定理对于我们判断魔方群子群的阶数很重要。
九、生成元
我们说，魔方群是置换群的一个子群。但是这样看和我们的魔方操作关系并不大。从另一个角度看，魔方群其实是一个由六个基本操作<U,F,D,L,R,B>生成的群。
什么意思呢？如果我们有一个群G，且其中所有元素都可以由群G中的某个元素通过与它自身的复合构成，那么这个元素称为这个群的一个生成元。例如群{1，i,-1,-i}配上乘法，那么其中每个元素都可以由i复合而成，因此i是这个群的一个生成元。同时，-i也是这个群的生成元，但是-1，1都不是这个群的生成元。
一个群也可以有多个生成元。我们把多个生成元称为群的生成集合：群G的生成集合是子集S 使得所有 G 的所有元素都可以表达为 S 的元素和它们的逆元中的有限多个元素的乘积。我们把集合S生成的群记为<S>。如果 S 是有限的，则群 G = <S> 叫做有限生成群。注意一点，有限生成群并不一定是有限群，它只是说这个群有有限个生成元。举个例子，由1和加法可以生成整数，因此（Z,+）是一个有限生成群，但是它是无限群。（我们常把群G表示为（G,*）其中*为定义在群G上的二元运算）
我们把群G的生成集合的元素个数的最小值称为群G的秩。 比如群{1，i,-1,-i}配上乘法，其秩为1，（Z,+）的秩为1。
我们把秩为1的群称为循环群。循环群具有以下结构：
对于同一个群，我们可以选取不同的生成集合。比如（Z,+）可以由1生成，但也可以由
如果我们从生成元的角度看魔方群，那么魔方群就是由6个生成元生成的群，即R=<F,L,D,U,B,R>。（我们常用R表示魔方群，因为魔方英文是rubik's cube）
十、群的展示，Cayley graph
直接研究魔方群有些复杂，我们先研究魔方群的子群。
魔方群的比较小的非平凡子群是什么？很自然能想到由一个操作生成的循环群：<F>。（注意，这不是最小的非平凡子群，请读者想想，还有什么非平凡子群更小？）但我们仅仅知道这个群是由一个生成元生成是不够的，还需要其他限制条件我们才能确定一个群的结构。显然，我们的限制条件是
我们可以举个例子：之前提到过的正多面体的对称群
我们可以看看魔方群的一些稍微复杂一点的子群。首先，我们得了解，魔方群的子群有什么条件？之前我们已经推导出，魔方群的阶数为43252003274489856000，如果我们把它因式分解，我们可以得到
我们有Lagrange's theorem，也有与它相对的Sylow theorems。Sylow theorems保证，对于G的阶数的某些因数，会有对应此因数的子群存在，且会给出有关此类子群的数目的相关信息。 在这里我们仅介绍Sylow第一定理：
如果群G是阶数为
也就是说魔方群一定包含阶数为11的子群，阶数为2的子群，但不一定包含阶数为6的子群。（但其实是包含的，只不过Sylow第一定理不保证而已,例如操作FLDUBRFLDUBR作为生成元生成的群）
那么聪明的你能找到阶数为11的子群吗？没错，我们只需要找到一个11阶置换就可以了。我们可以用第一篇文章一开始给出的软件中的input cube做到，只要设定一个合理的11阶置换。
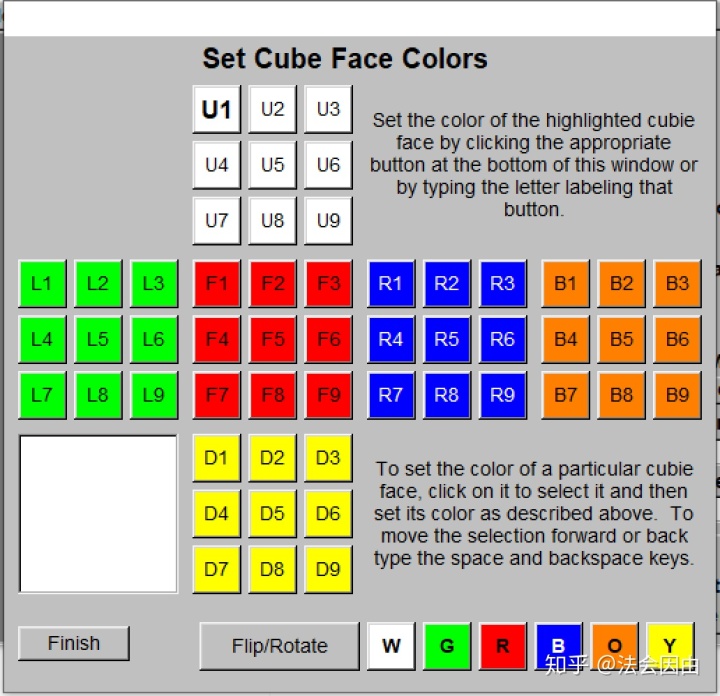
接下来我们思考，某一个操作的阶数和由这个操作作为生成元形成的群的阶数是一样的吗？请读者自己思考并证明。关于操作的阶数，还有一点是，如果操作P的阶数是m，有任意一个操作Q，那么P关于Q的共轭
接下来我们看看一些非循环群的情况。例如，由{FF,RR}生成的群。这个群有两个生成元，我们将其记为：
有读者可能会问，明明这两个操作不是交换的，那么我们要不要在群的展示里加上
故
那么这个群里有多少个元素呢？
首先，由于这两个操作都是二阶的，那么他们肯定不能相邻，这样一下就把可能性缩小到了18种：
但是这18种还有没有重复的？
如果我们仔细考察，我们会发现
根据逆元的唯一性，我们可以得到：
实际上，去掉重复的元素，我们只剩下12个元素：
那么这些群元素之间的关系是怎么样的呢？在群论中我们往往用一种有向图来表征群元素之间的关系，这就是Cayley图。例如群
这个图的含义简单易懂，前一个元素乘以F（生成元）以后可以获得箭头后的元素。
那么群
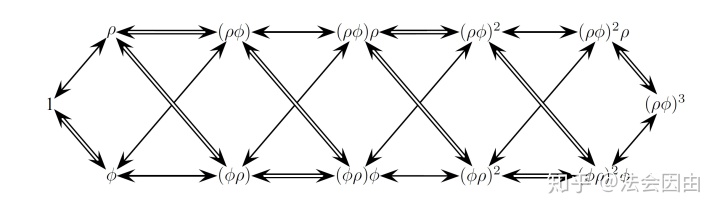
在图中，单箭头表示可以通过乘
同一个群，如果选择不同的生成元，得到的Cayley图也不一定一样。之前我们说，群（Z,+）可以选择把1当做生成元，也可以把2和3选成生成元。请读者分别画出他们的Cayley图。
别的群呢？我们看看四阶偶置换构成的群
如果把它们全都列出来：
(1)、(1 2 3)、(1 2 4)、(1 3 4)、(2 3 4)、(1 3 2)、(1 4 2)、(1 4 3)、(2 4 3)、(1 2)(3 4)、(1 3)(2 4)、(1 4)(2 3)
猜猜这个群有多少个生成元？事实上，这个群只需要两个生成元便可生成整个群：（1 2 3）和（1 2 4）。它的Cayley图长得比较玄学：
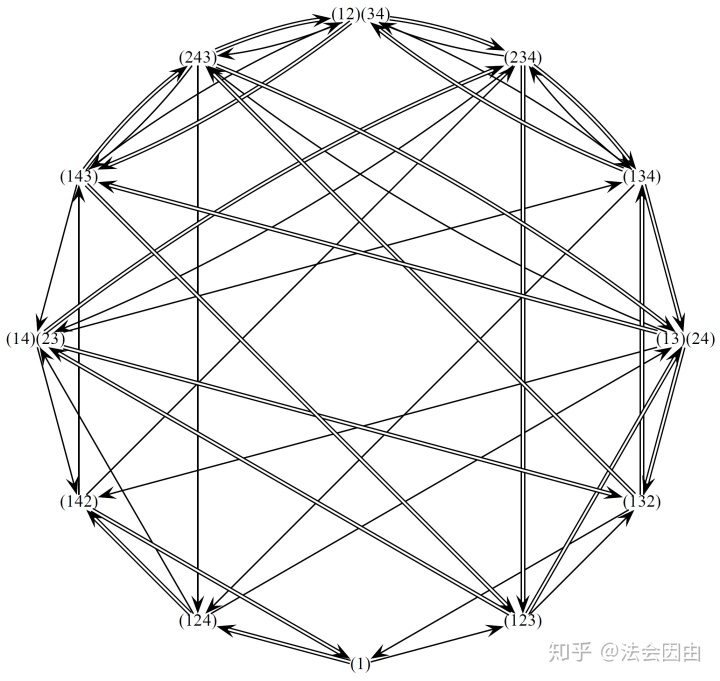
Cayley图是证明著名的巴拿赫-塔斯基悖论（分球悖论）的关键因素。
这群论怎么学着学着就变成图论了呢？实际上，几何群论就是这样一门学科，它用图形研究离散群。它先把有限生成的离散群转化为其Cayley图，再通过图度量视为度量空间，然后就可以用度量几何学的方法进行研究，与双曲几何、大尺度几何等都有密切联系。
代数如果离开了几何就失去了生命力，了无生趣——恽之玮
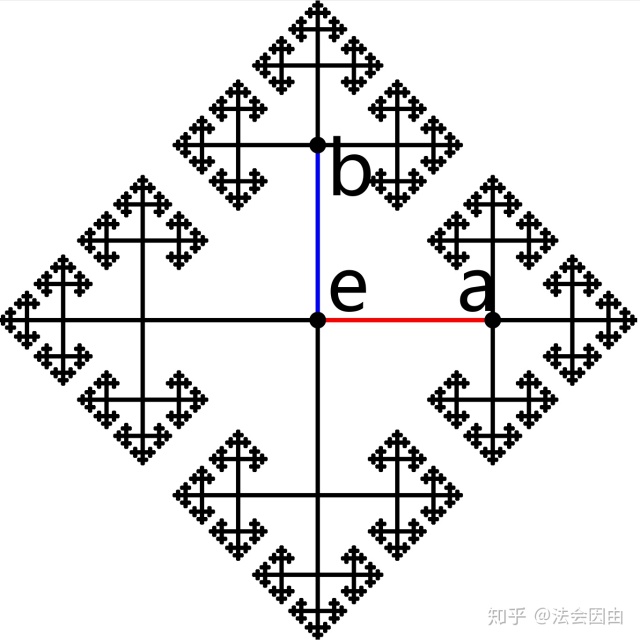
除了这两个简单群以外，别的群呢？我们能不能通过知道一个群的展示从而推出一个群的阶数？很遗憾，在总体来说这是不可能的，我们只能研究具体的群。比如由F和R两个操作生成的群，它有几阶？
操作FR的阶数为105（可以通过写出其facelet置换来求出，也可通过软件，也可通过直接转魔方求出。不过魔方操作阶数的最大值为1260，万一碰到阶数超高的就不太实用），我们有这个群的一些关系：
这个群有多大呢？这个群有
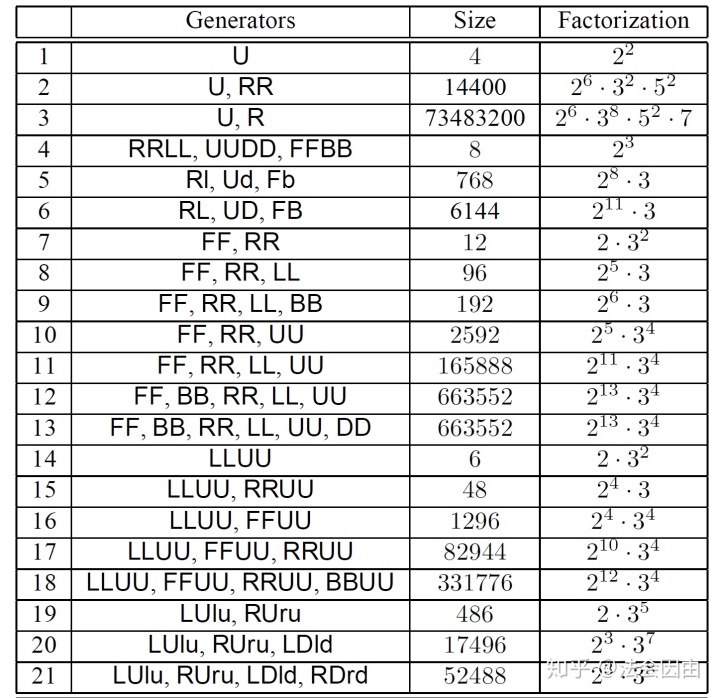
可见只需要很少的生成元，群就可以变得非常大。另外我们可以发现12和13行中虽然增加了DD这个生成元，但群的阶数并没有变，说明这个生成元可以由别的生成元生成（这个生成元真是个DD）
虽然在总体上我们没办法通过一个群的展示求出一个群的阶（Order of a Group from its Presentation）但是针对魔方群及其子群，我们可以用软件（例如GAP）计算出这个群的阶：Analyzing Rubik's Cube with GAP
我们把魔方的每个facelet用数字代替，然后每个基本操作都可以用数字的置换表示：
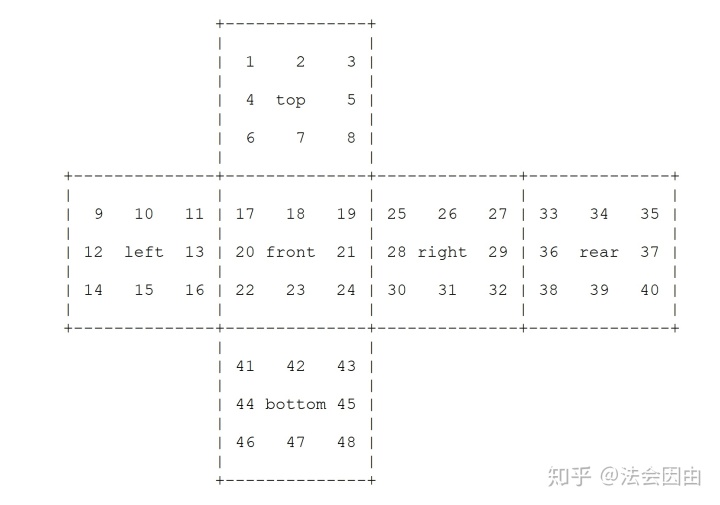
然后在程序里写上六个生成元：
gap> cube := Group(
> ( 1, 3, 8, 6)( 2, 5, 7, 4)( 9,33,25,17)(10,34,26,18)(11,35,27,19),
> ( 9,11,16,14)(10,13,15,12)( 1,17,41,40)( 4,20,44,37)( 6,22,46,35),
> (17,19,24,22)(18,21,23,20)( 6,25,43,16)( 7,28,42,13)( 8,30,41,11),
> (25,27,32,30)(26,29,31,28)( 3,38,43,19)( 5,36,45,21)( 8,33,48,24),
> (33,35,40,38)(34,37,39,36)( 3, 9,46,32)( 2,12,47,29)( 1,14,48,27),
> (41,43,48,46)(42,45,47,44)(14,22,30,38)(15,23,31,39)(16,24,32,40) );
<permutation group with 6 generators>然后最基础地，我们可以知道这个群的大小：
gap> Size( cube );
43252003274489856000当然我们也可以用它来解决魔方，即将置换分解成六个生成元的复合：
gap> f := FreeGroup("t","l","f","r","e","b");
<free group on the generators [ t, l, f, r, e, b ]>
gap> hom := GroupHomomorphismByImages( f, cube, GeneratorsOfGroup(f),
> GeneratorsOfGroup(cube) );
[ t, l, f, r, e, b ] ->
[ (1,3,8,6)(2,5,7,4)(9,33,25,17)(10,34,26,18)(11,35,27,19),
(1,17,41,40)(4,20,44,37)(6,22,46,35)(9,11,16,14)(10,13,15,12),
(6,25,43,16)(7,28,42,13)(8,30,41,11)(17,19,24,22)(18,21,23,20),
(3,38,43,19)(5,36,45,21)(8,33,48,24)(25,27,32,30)(26,29,31,28),
(1,14,48,27)(2,12,47,29)(3,9,46,32)(33,35,40,38)(34,37,39,36),
(14,22,30,38)(15,23,31,39)(16,24,32,40)(41,43,48,46)(42,45,47,44) ]例如...
gap> PreImagesRepresentative( hom, z.1 );
l^-1*t^-1*e^-1*t^2*e*l*f*r*t^-1*r^-1*f^-1*t*f*r*t*r^-1*t^-1*f^-1*t^
-1*f*t*l*t*l^-1*f^-1*l*t^-1*l^-1*f*r*t^-1*r^-1*f^-1*l*t*f*t^-1*f^
-1*l^-1*t*f^-1*l^-1*t^-1*l*t*f*t^-2*f*t*f^-1*t^-1*l^-1*t^-1*l*t^-1*l^
-1*t*e^-1*t*e*l*t*l*t*e*l^-1*e^-1*t^-1*l^-3*b*f*b^-1*l^-1*f^-1*t*l^
-1*f*t*f*l^-1*t^-1*b*r^-1*b^-1*t^-2*e^-1*r*e*r*f^-1*e*t^-1*e^-1*r^
-2*t^-2*l^-1*b^-1*r^-1*e^-1
gap> Length( last );
106当然这个软件还能做很多很多事情，就不在这里一一介绍了。有兴趣可以去官网下载学习这个软件。
十一、群同构，群直积
刚刚我们一直在从生成元的方式看群，而从这个角度看，魔方群在这个意义上并不是置换群，而是一些操作的集合，但是这两个群本质或者群的结构是一样的，我们把这样的关系称为“同构”(isomorphism)。用数学语言表示，便是：如果有两个群
那么我们称这两个群同构。注意同构要满足双射，如果只是一个映射那么这个则是群同态（homomorphism）。有人常常分不清同态(homomorphism)与同胚(homeomorphism)，大概因为这两个词是同胚的吧（笑
如果两个群是同构的，那么这两个群基本上是一样的，因为它们具有相同的代数结构。从群的角度不需要区分。你知道有哪些群是同构的？比如一开始我们介绍的三阶置换群和正三角形的对称群同构，克莱因四元群，它和四阶的二面体群
什么是模二加法群？这个群的集合里为数字，数字之间的二元运算为，两者相加以后再取除以2的余数。自然，这个群只有两个元素，{0,1}，请问单位元是谁？
再看模5加法群：其中有四个元素{0,1,2,3,4}，而1是这个群的生成元：
1 = 1, 2 = 1 + 1, 3 = 1 + 1 + 1, 4 = 1 + 1 + 1 + 1 ， 0 = 1 + 1 + 1 + 1 + 1。这个群还有别的生成元吗？
有模n加法群，自然也有模n乘法群，它有0到n-1这n个元素。但是只当n是质数时，它才构成群。例如当n=6的时候，2没有逆元：2 ∗ 1 = 2, 2 ∗ 2 = 4, 2 ∗ 3 = 0, 2 ∗ 4 = 2 ， 2 ∗ 5 = 4。想想n是质数的时候，这个群的单位元，每个元素的逆元是什么？
刚刚我写到，克莱因四元群和两个模2加法群的直积同构。在这里，群直积就是笛卡尔积，给每两个群里的元素配成有序对。（在群的意义下，直积和直和相等）
如果我们有两个群，
两个群的直积也是一个群。请读者自行验证这直积群满足四条公理。
那么群直积在魔方中有什么体现呢？如果两个群的生成元彼此互不相干，那么把两个群的生成集合的交集作为生成集合的群与原来两个群的直积群同构。
例如，由操作F生成的群和操作B生成的群互不相干，那么由操作F,B生成的群和原来两个群的直积同构。这样我们就可以很方便地计算群元素的个数：原来两个群的阶数都是4，直积以后则变成16。还有很多不相干的操作，例如翻转两个棱块的操作和交换两个角块的操作互不相干，他们构成的群也是直积群。
十二、降群法解魔方
所谓的降群法就是改变魔方的生成元，从而减少魔方可能的状态数。普通的方法都是从部分到整体，一层一层或先角后棱，但是降群法是直接从整体入手，减少魔方的状态数，看起来每一步都是乱转，没有一面或者一层是好的，但最后寥寥几步复原。方法最初出自：Human Thistlethwaite Algorithm
思路是这样的：
本来的魔方群有六个生成元：
通过一些操作（可以随意转动），我们把当前魔方的状态转到由生成元
随后通过另一些操作（左右只能180°，如果要转90°必须在不影响棱块定向的基础上做逆操作），我们将魔方的状态转到由生成元
然后我们再把魔方群进一步降阶，降到由生成元
最后一步我们甚至可以通过直觉还原，将群降到单位元生成的群
至于具体的做法，怎么降到下一步所要的群中，网上有具体教程。可参考：最酷的玩法：Thistlethwaite Method，附word文档 - ★ 其他速解法 (Other Methods) - 魔方吧·中文魔方俱乐部 - Powered by Discuz!
或者降群法详解 - ★ 其他速解法 (Other Methods) - 魔方吧·中文魔方俱乐部 - Powered by Discuz!
或者状态集转换法学习笔记 - ★ 其他速解法 (Other Methods) - 魔方吧·中文魔方俱乐部 - Powered by Discuz!
1992年，Kociemba's algorithm改进了上述的 Human Thistlethwaite Method。他把
当然，除了这种降群法以外，还有别的改变生成元的办法。但是上述提到的这种更为常用。
不过其实5个生成元和六个生成元构成的群其实是一样的：
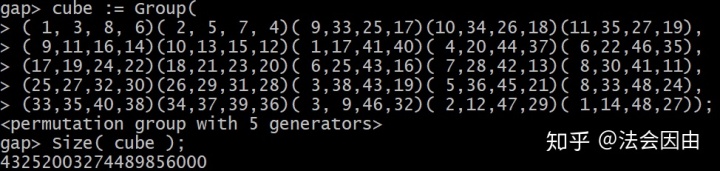
再减少一个生成元的时候，即由四个生成元生成的群：
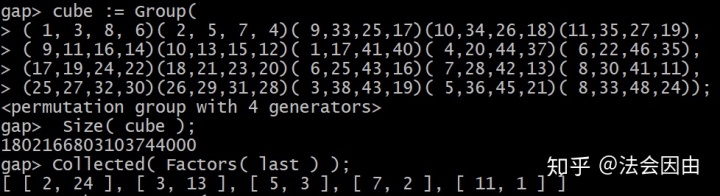
我们可以发现减少因子为24（2*2*2*3），减少得不算多。
如果我们再减少一个生成元：
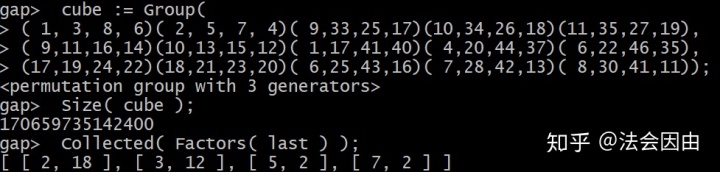
我们发现减少因子为10560（
我们已经知道由两个生成元生成的群的阶数为
如果我们变着法改变生成元，比如先减少U和D。：
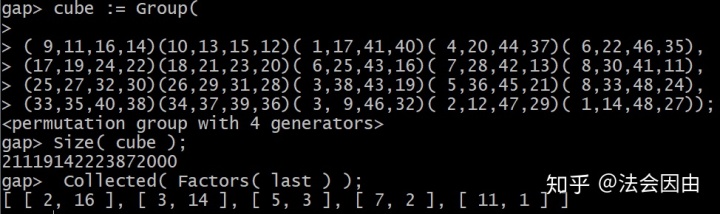
减少因子为2048，我们发现它与降群法第一步减少的因子是一样的：
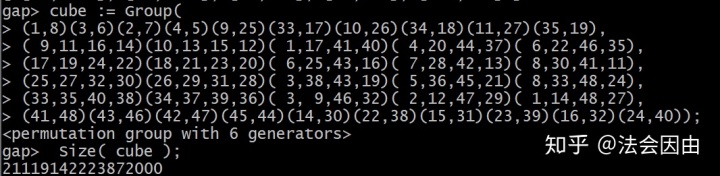
这说明...
再减少一个生成元的话：
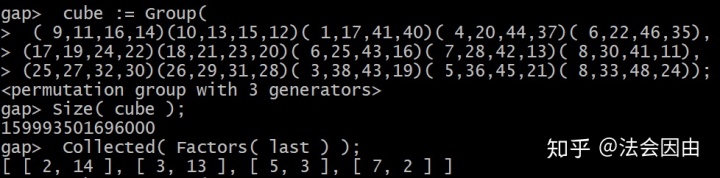
好像不是很明显。但是如果我们能再减少F的话......很显然效果拔群。但是这种方法相比原来的不太容易看。
当然，你也可以创造自己的减少生成元从而神奇解决魔方的办法！
大概就写到这里了。感谢全部看完的读者并且认真做练习的读者！如果文中有问题不会可以问我~有的我只是不想写了所以读者自证不难了（笑
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
