本文介绍三角函数的基础知识，包括弧度的认识、弧长与扇形面积的计算、任意角的概念及三角函数的定义，并介绍了诱导公式及其应用。
三角函数是高中数学的重要内容，无论是国内还是国际三大体系，AP、IB、Alevel中都有三角函数的一席之地，而且要求不低，比如ALevel Further Math要求掌握利用积化和差求积分，（这一点可以参看《三角函数积分方法总结》）。而且三角函数还会和求导、积分、复数等联系在一起，所以学好三角函数非常重要。
本文主要讲解以下五个知识点：
1.认识弧度
2.弧长与扇形面积计算
3.角度的推广，任意角
4.任意角下的三角函数
5.诱导公式
一、认识弧度
在初中我们用度(°)来衡量一个角的大小。就像克、千克、吨等同样衡量质量一样，我们现在引入弧度(Radian)来衡量一个角度的大小。那么1弧度角有多大呢？
弧长为半径长的弧所对的圆心角为1弧度。
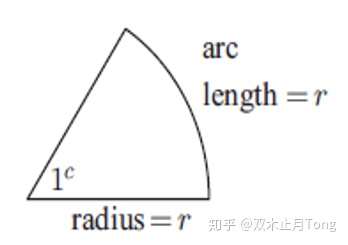
半径为
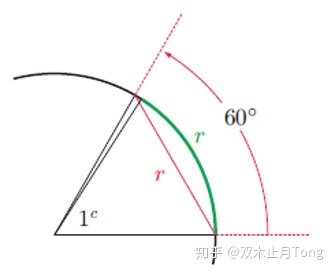
根据弧度的定义以及
常见的比如：
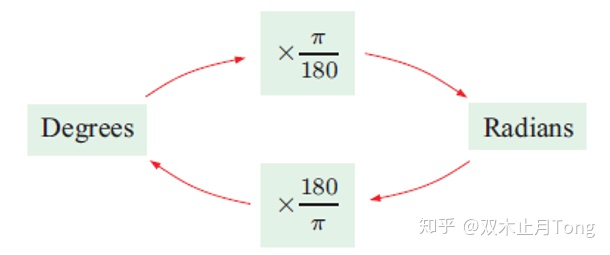
注：以后数字右上角没有"o"的都默认在弧度制下面。
二、弧长与扇形面积计算
那么为什么要引入弧度制？
第一个引入弧度制能够帮助我们简化一些运算，比如接下去讲的扇形弧长与面积的计算。
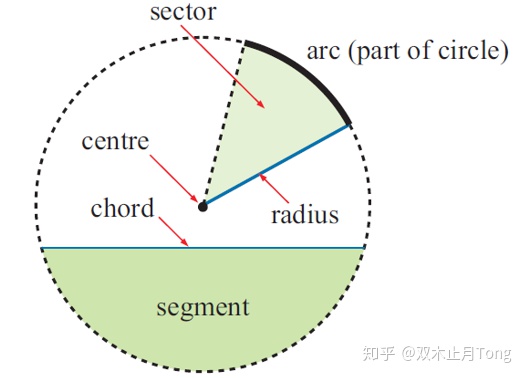
在度制下，我们是利用成比例的方法来求解弧长与面积的，也就是算出圆周与圆面积，然后根据角度大小求出占比，从而求得对应的弧长与扇形面积。不过，引入弧度制后，我们有了更加简单的公式如下：
注： 扇形面积公式
当然引入弧度不仅仅是为了便于计算扇形弧长与面积，而是把我们的实数与角度建立起了一一对应的关系，把初中所学的三角函数定义域从
三、角度的推广，任意角(General angle)
如果在初中被问到：请画出一个大小为
我们肯定是一脸问号……我们学的角度不都是正的吗？怎么还出现负的了？？
如果我们还是像初中一样在直角三角形中去定义角度大小，那么肯定是画不出负角度的。因此，我们这里要重新给出角大小的定义。接下去我们用旋转来定义一个角度的大小：
我们规定x轴正半轴为始边，逆时针旋转为正、顺时针旋转为负，如果逆时针旋转
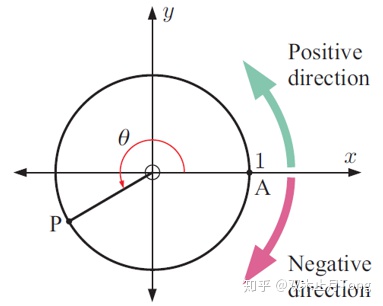
所以，你要画一个
至此，无论什么角我们都能够画出来了，大不了多转几圈就可以了。
四、任意角下的三角函数
在讲解任意角的三角函数之前，我们先简单回顾一下初中是如何定义三角函数的。
初中三角函数是在一个直角三角形中定义的，有一个直角三角形
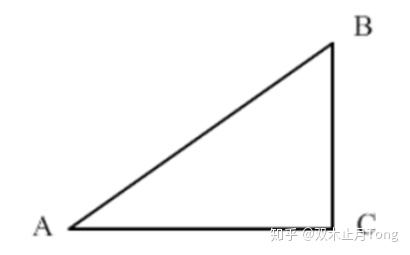
那么如何定义任意角下的三角函数呢？
在上一小节中我们知道了任意角有一条始边与终边，类似的我们也可以定义三角函数。不妨设终边最后落在了第二象限上，如下图所示。
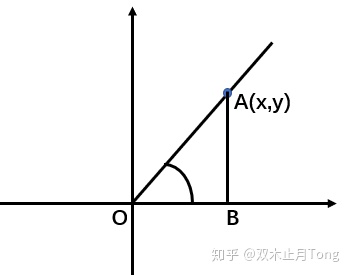
然后过点A作x轴的垂线，垂足为B，那么我们就有了一个直角三角形
类似的，无论终边落在那个象限上我们都可以利用在终边上取一点，做垂线来定义三角函数。并且，在终边上任意取一点，最后得到三角函数值是一样的。因为
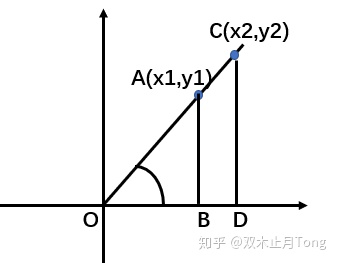
但是这样子计算三角函数值也太复杂了，在终边上任取一点坐标，要算到原点的距离还需要求比值。
所以为了简化我们的计算，引入了单位圆。
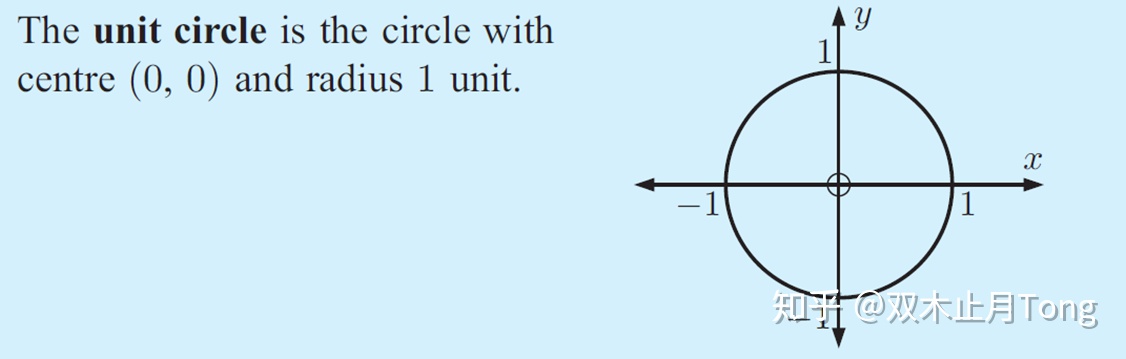
圆心为原点、半径为1的圆称为单位圆。
那么引入单位圆后有什么好处呢？
我们可以过终边与单位圆的交点作垂线，求对应的三角函数值。因为圆周上的点到圆心的距离为1，于是
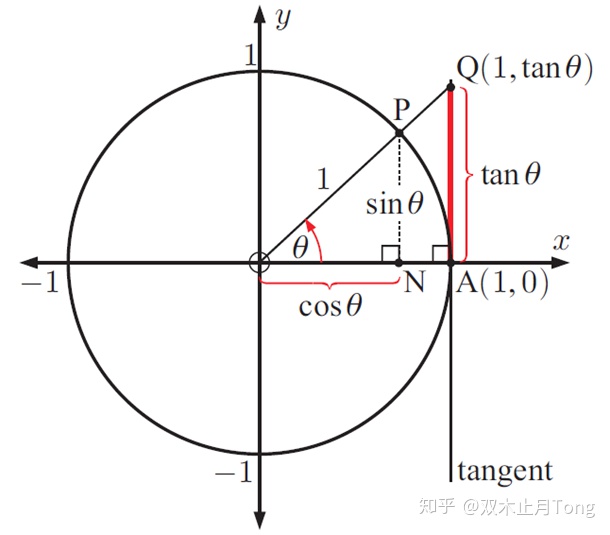
无论
于是，我们计算任意角的
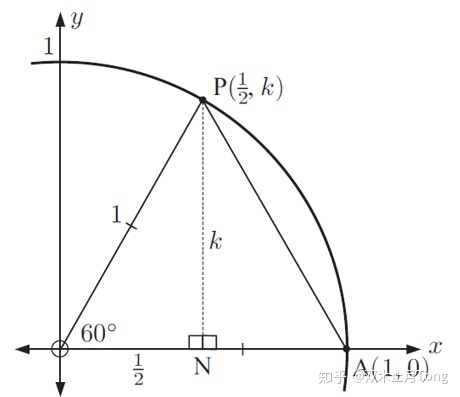
根据勾股定理得
在直角三角形中我们没有办法知道
五、诱导公式
三角函数是具有周期性的，比如终边再原来的基础上再转
下面是一些常见的转化公式：
公式一：
公式二：
公式三：
公式四：
公式五：
公式六：
上述公式是弧度制版的角度转化公式，当然还有角度制版的转化公式。
但是真的有必要把上面公式一个一个记下来吗？
其实是不用的，我们只需要记住下面十字口诀就可以了：
奇变偶不变，符号看象限
首先我们把需要转化的三角函数整理为标准形式：
接下去判断
（1）如果是偶数，那么
![]()
（2）如果是奇数，那么
![]()
这样前半句就结束了，那么后半句就是要在得到的三角函数前面要加个正负号。
那么到底加正好还是负号呢？
这是由
(1)如果是正的那么诱导出来的三角函数就是正的，“+”号我们就不标出来了；
(2)如果是负的那么诱导出来的三角函数前面还要添加一个负号。
不过要注意的是，这里的
比如
（1）,那么
,所以要变，
；
（2）是先逆时针旋转
然后再顺时针旋转一个锐角，因此终边落在了第一象限上，而
看的是x值，是正的，于是
。
再比如
（1）这是，
，是偶数，所以不变，
；
注：要转化为标准形式。
（2）是顺时针旋转一个锐角度，那么终边落在了第四象限上，而第四象限上
是负的，所以
。
关于各类三角函数在各象限的正负性，我们可以画图判断。在国际教材中还有一句口诀叫“ASTC”，分别对应四个象限：
（1）第一象限，A，也就是ALL，所有的都是正的；
（2）第二象限，S，也就是Sin，只有是正的；
（3）第三象限，T，也就是Tan，只有是正的；
（4）第四象限，C，也就是Cos，只有是正的。
记口诀或者画终边都可以判断三角函数的正负性，两种方法都可以。
上述内容都是比较基础的知识，三角函数的内容还有很多，比如在下文中我们用两种方法证明了两角和差公式，并以此讲解了二倍角公式、辅助角公式、和差化积与积化和差：
双木止月Tong：【“数”你好看】三角函数两角和差公式zhuanlan.zhihu.com
欢迎交流讨论~
想了解更多国际数学课程的知识，可参阅：
双木止月Tong：【国际数学课程】目录zhuanlan.zhihu.com
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
