树状数组 区间加 区间求和_关于求和的一些思考

最新推荐文章于 2024-06-17 23:09:11 发布
最新推荐文章于 2024-06-17 23:09:11 发布 · 361 阅读 · 2
文章标签：

#树状数组 区间加 区间求和

本文介绍了和式的基础及其在数学中的应用，包括等差数列和等比数列的求和方法，如倒序相加法和错位相减法。此外，还探讨了前缀和、差分的概念以及在解决区间求和问题中的应用。通过不同的视角，如模拟展开、变换思考和升维打击，解析复杂的求和公式，展示了求和在解决实际问题中的智慧和灵活性。

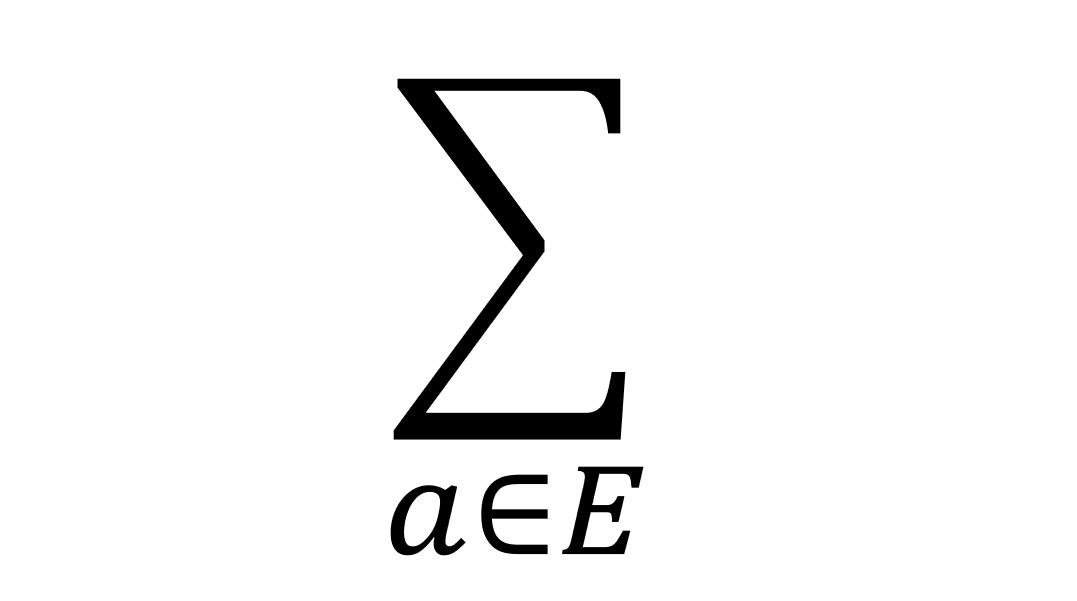
20471a8d25531edb7c72e5a9e224fef9.png
title: 关于和式的一些基础
tags:
  - 数学
categories:
  - 总结
mathjax: true
date: 2020-11-08 23:20:23

全文见

这里.​shzaiz.github.io

知乎不支持$$的TeX. 真屑.

印象中, 我对于求和记号的探索好像是一点一点摸索出来的. 也没有人教我一些和式变换的技巧. 对于我而言, 一些我本应该会的东西到现在才会.

<!--more-->

求和记号基础

印象中, 我对于求和记号的探索好像是一点一点摸索出来的. 也没有人教我一些和式变换的技巧. 对于我而言, 我认为和式对于新手而言是十分重要的. 那么今天, 总结一些和式常见的变换技巧以及相关知识点.

求和记号一般只是一个工具. 更加优秀想法就是直观理解这个求和记号表达的意思.

这是求和记号,最最基本的用法是这样子:

​表示下界, ​表示上界, ​从​开始取数, 一直取到​, 全部加起来。

也就是for(int x = i; x<=n;x++) ans+=k;.

有时候这个​只有下边有东西. 这样子的话, 我们需要对于所有满足条件的东西求和. 比如这个:

假设​是图中的一条边.就是说对于所有的从​到​的边. 其中​都是变量, 在后面的和式中可能会被替换. 具体是什么东西, 那就要看具体情况了.

总结:求和记号的常见两种方式是

  • ​ 表示ans值:for(int i = k; i<=n;i++) ans+=f(i);.
  • ​ 表示ans值: for(cond(i)) ans+= f(i);.

一些基础的求和方法

上面大致笼统的说了一下求和. 看不太明白也没关系.下面我们来据一些例子加深一下理解. 这些例子不会太难, 都是文化课的例子. 先稍微感受一下.

例子0. 一些公式

公式1. ​.

相关证明既可以待定系数做, 也可以用立方和公式做, 也可以猜想. 在这里就不在详细说了. 相关证明方法见这里. 个人推荐证明上述方法2.

公式2. ​

经过上述方法的讯熏陶, 我们发现需要证明二次的东西, 需用三次的展开. 那么证明三次的, 就需要用四次的展开. 这里写出​. 并且仿照刚刚的步骤​. 对于上面的式子求和, 接下来可以推出:

例子1. 倒序相加法

对于这个方法, 最具有典型性的就是等差数列的求和了. 等差数列, 就是从第二项起, 每一项与它的前一项的差等于同一个常数的一种数列. 这个常数叫做等差数列的公差, 公差常用字母​表示. 这个就是大家熟知的“等差数列的和=(首项+末项)×项数÷2”.

形式化的, 用刚刚的求和记号写出来就是:​.

例子2. 错位相减法

对于这个方法, 最具有典型性的等比数列求和了. 通过乘上一个​, 我们就可以轻松的消去中间一大堆东西. 从而得到求和公式为​.

运用求和的例子

在OI中, 我们有许多地方可以用到求和和求和的性质.

前缀和

简单来说,前缀和是一个数组的某项下标之前(包括此项元素)的所有数组元素的和.形式化的说, 一维的前缀和可以这样用:

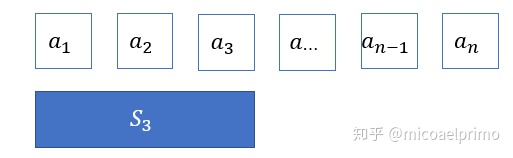
8f6f3d6b9bb7e5cc388f8f8fe3d40175.png

所以, 当式子中出现​的时候, 就可以想到用一维的前缀和进行优化. 相比暴力每次​的复杂度, 这里可以轻松的降低到​.(预处理需要​).

如果换做更高维度的前缀和, 比如二维前缀和, 求得一个元素的值有什么变化?

定义在可预见的范围内加了一维度.

这里的前缀和​数组就相当于从​到​的子数组的和.

如果要求任意子矩阵的和的话, 我们可以用这个图示:

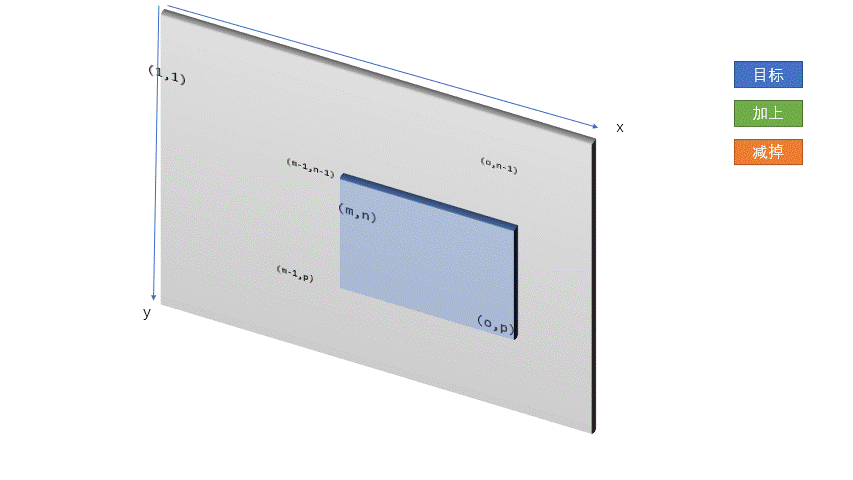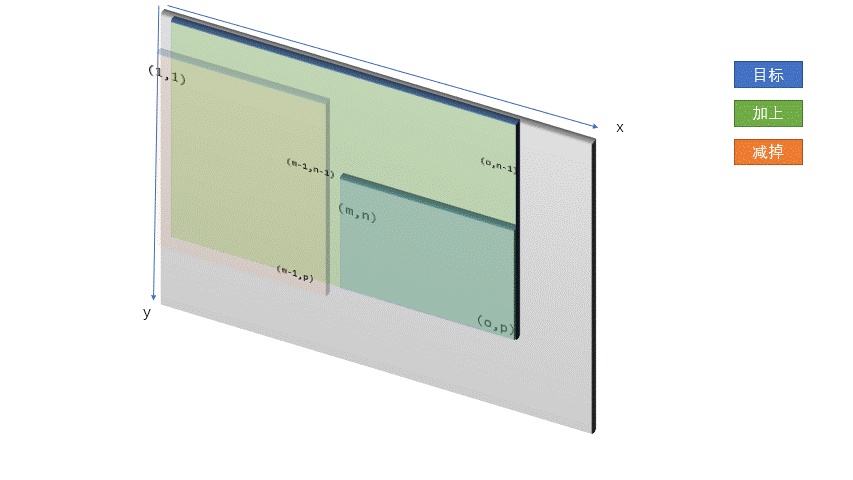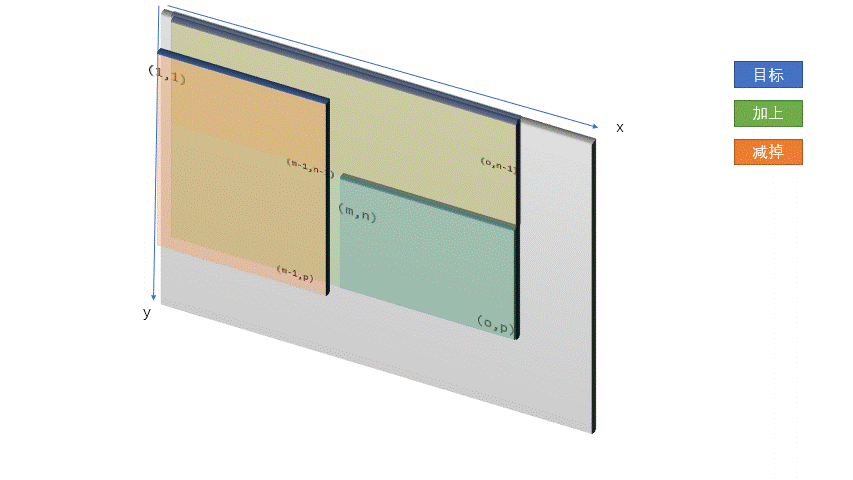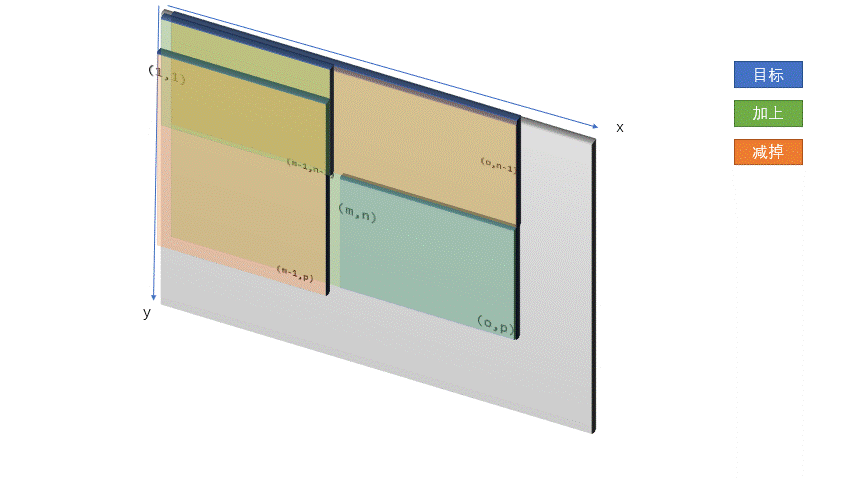
59e76c748c76efc1110b8b86701a08f3.png

代码是b[x2][y2]+b[x1-1][y1-1]-b[x1-1][y2]-b[x2][y1-1].

差分

差分的结果反映了离散量之间的一种变化.

引入:给出n个数, 再给出Q个询问, 每个询问给出l, r, x, 要求你在l到r上每一个值都加上x, 而只给你O(n)的时间范围, 怎么办？

概念: 简而言之, 区间加变化少的是前后之间的差值. 所以我们认为​.

比如我们要把第​到​加上一个数字, 那么就​加上, ​减掉. 查询的话找到前缀和就是原数列.

二维形式的差分.

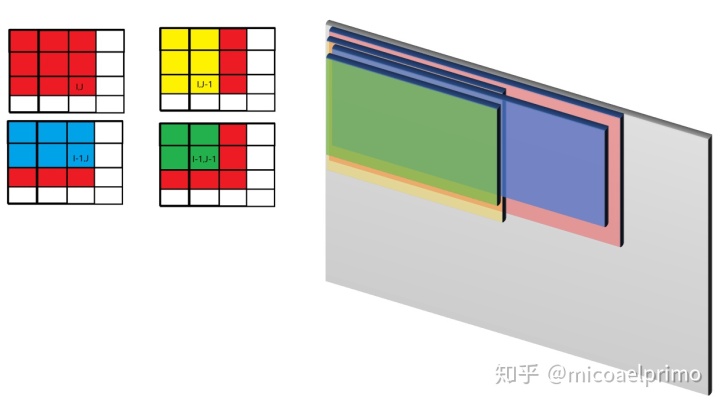
4c4a5ad2d4cf51675ac15efab267e044.png

如果我们从左到右, 从上到下的遍历, 当要求红色部分, (0,0)到（i,j）处的前缀和时, 我们黄色部分和蓝色部分已经是已知的了.而它们重叠的部分就是绿色部分, 所以把黄色和蓝色部分的结果加起来, 再减去绿色部分, 最后加上(i,j)处的值就是（i, j）位置的前缀和了.

因此sum[i][j]=a[i][j]+sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1].

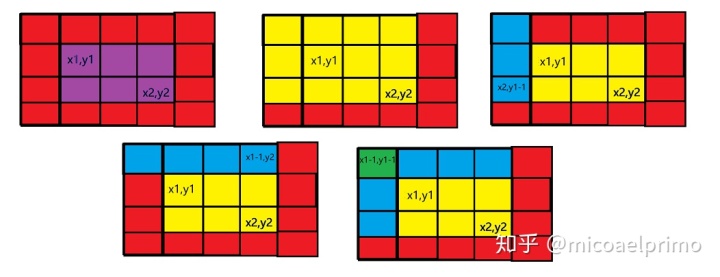
0af45600660ef8c6aca38da29b15cd16.png

我们要求紫色部分的值，我们已知的是黄色部分的值，但它多了两个蓝色部分的值，而两个蓝色部分有重叠了个绿色部分

所以要求的区间内的值就是sum[x2][y2]-sum[x2][y1-1]-sum[x1-1][y2]+sum[x1-1][x1-1].

换一种视角看求和记号

当求和下标变得非常复杂的时候, 我们就发现以前的方法几乎没有什么方法来帮助我们. 现在, 我们来思考几种方法让我们重新看清楚一些求和公式的真面目.

视角1. 模拟出奇迹

对于一些奇怪的求和公式, 我们可以先写几项展展看. 看一下会出什么样的结果. 注意留意相同的部分.

例子1.

假设这里面有三项吧. 那就是​. 思考一下暴力展开的结果. 把同类项的放在一起考虑. 可以发现, 答案就是

例子2.

下标变得复杂起来了. 不过应对这种下标, 我们可以认为这是在一个数列里面进行求和.

这是我在这个视角下的证明过程:

538d6a0f847c8332d4bffff89f9e5c63.png

稍微变一下,就不难得到右侧的式子.

例子3.

fd75fb514f59d1e9af0994eff1ac1824.png

这个也不难得到.

例子4.

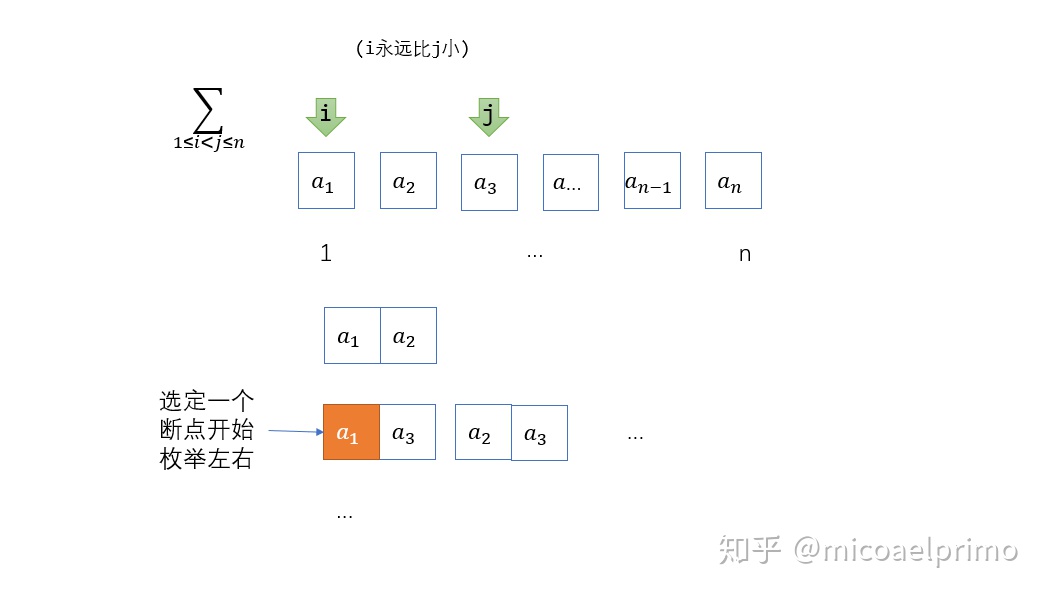
e50e2087edbd05011be4bcf51efb2d68.png

这个可以直观理解. 拆开之后发现左边这个也可以得到.

例子5.

如果暴力拆解一下会发现, 由于对称性, 后面的式子一定是前面式子的​.

例子6.

运用前缀和的思想, 可以轻松想到这个问题的答案.

视角2. 变换看的方式

(aka. 歪一歪头获得80智商)

例子7.

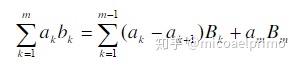
5b8be46318460dd7b6361d3d98127267.png

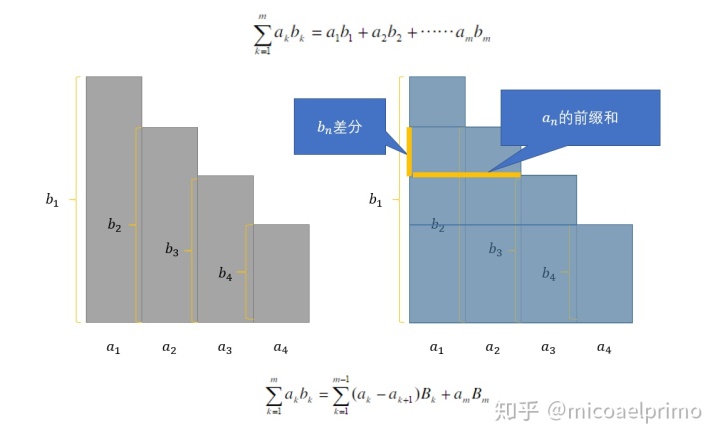
b3df8aa4e20494d73dda0e8dd0ddf434.png

这个方法在用树状数组维护的时候会用到.

例子8. 给定两个长度为​的数列​,​。共有m次询问，每次询问给出两个正整数​, ​，从​到​的区间设为​ 要求输出

的值.

考虑已经知道两个小区间的值. 左边区间的答案是​ , 右边区间的答案是​. 如何合并?

考虑一下平面上的点对. 可以发现合起来是 枚举左边的+枚举右边的+枚举跨中间的. 也就是说是这样的一个情形.

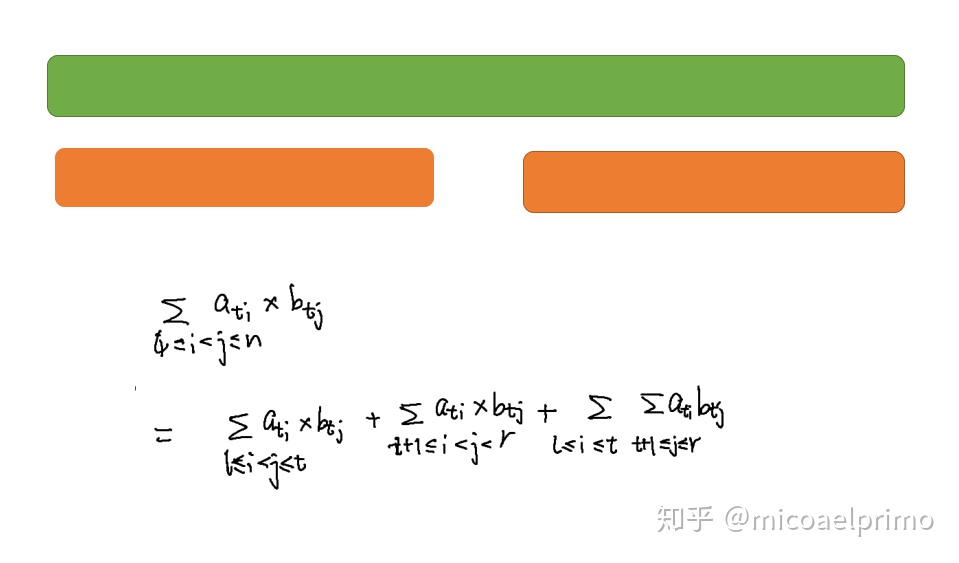
2d1dd8b76f8ce2e031e6acb1e1c83cf3.png

视角3. 升维打击

在这里, 我们可以把这些参量看作屏幕上的的点对.

例子9. 优化

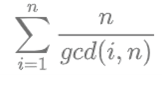
73a9b05e946afc41aca73387fb515aea.png

的过程.注意多组数据，T<=300000,n<=10000000.

推导回来再放, 其中​这一步就用到了刚刚说的升维打击.

[树状数组] 区间求和的三种模型
童凌的技术博客
07-22 2834
树状数组在区间求和问题上有很高的效率，尤其在非常困难的比赛中（数据量大，对时间限制很严格的比赛）能发挥非常大的作用，其各种复杂度都要比线段树低很多，而且其代码简洁优美……有关区间求和，主要有以下三个模型： (以下设a[1…n]为一个长为n的序列，初始值全为0)1、改点求段型：即对于序列A有以下操作： 求整段区间的和：给定i，计算a1+a2+…+ai 修改单点：给定x和c，执行ax += c 这是最
树状数组区间和、区间加减
weixin_45724872的博客
09-05 1120
题面 题目 分析 如果用线段树做那就是裸题了，但是用树状数组我们需要转化一下； 首先看到区间加，我们考虑使用差分； 对于差分数组来说，维护区间加是很容易的，只需要单点修改； 那么我们看看区间和有什么规律； 比如求区间[L,R][L,R][L,R]的和，则是aL+...+aRa_L+...+a_RaL​+...+aR​ 那么对于差分数组b来说，则说∑i=LR∑j=1i\sum_{i=L}^{R} \sum_{j=1}^{i}∑i=LR​∑j=1i​; 这个是暴力求法，会TLE的； 我们将这个式子画出来，见
树状数组 区间加 区间求和_数据结构之真别多想—树状数组
weixin_39871649的博客
10-22 431
数据结构之真别多想—树状数组瓶颈如何理解树状数组？这个结构的思想和线段树有些类似：用一个大节点表示一些小节点的信息，进行查询的时候只需要查询一些大节点而不是更多的小节点。最下面的八个方块就代表存入 a 中的八个数，现在都是十进制。他们上面的参差不齐的剩下的方块就代表 a 的上级—— c 数组。很显然看出： c2 管理的是 a1 & a2 ； c4 管理的是 a1 & a2 &amp...
树状数组 区间加 区间求和_区间查询（树状数组和线段树）
weixin_39966765的博客
11-23 647
本文是LeetCode 307. Range Sum Query - Mutable的题解，主要是对树状数组（Binary Indexed Tree）和线段树（Segment Tree）的学习。本文首发于我的博客，传送门1. 问题描述Loading...​leetcode.com初始时给定一个大小为n的整数数组nums，设计两个方法：sumRange(i,j): 求区间[i, j]之间的元素和（0...
树状数组 [区间加区间求和]
FSYo 的博客
12-15 1477
考虑差分  设  那么   假设我们要求   那么 sigma 中间的定值可以提出来   于是维护两个差分数组 di 与 i * di #include&lt;bits/stdc++.h&gt; #define N 100050 #define LL long long using namespace std; LL t1[N],t2[N]; int n,m; void Up...
树状数组区间加区间求和
dbsaf26628的专栏
07-09 464
一般说来，树状数组比线段树好写得多，可是只用于单点修改。 然后最近学到一种区间修改的方式，区间加区间求和。 这里我们不直接维护原数组，而是引入另一个数组b[i]，表示和前一个数的差是多少。 这样的话a[i]就可以表示为b[1]+b[2]+b[3]……b[i]，相对应的，sum(i)就是b[1]+b[1]+b[2]+b[1]+b[2]+b[3]……b[1]+b[2]+b[3]…b[i...
精选资源
一个简单的整数问题2(树状数组：区间查询&&区间修改)
01-03
给定一个长度为N的数列A，以及M条指令，每条指令可能是以下两种之一： 1、“C l r d”，表示把 A[l],A[l+1],…,A[r] 都加上 d。 2、“Q l r”，表示询问 数列中第 l~r 个数的和。 对于每个询问，输出一个整数表示...
【模板】树状数组 区间修改，区间求和 （模板题：洛谷P3368树状数组2）
Dance Of Faith
05-26 716
题目描述 如题，已知一个数列，你需要进行下面两种操作： 1.将某区间每一个数数加上x 2.求出某一个数的和 输入输出格式 输入格式： 第一行包含两个整数N、M，分别表示该数列数字的个数和操作的总个数。 第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。 接下来M行每行包含2或4个整数，表示一个操作，具体如下： 操作1： 格式：1
树状数组区间修改区间求和
05-31
树状数组可以用来维护区间修改区间求和的问题。具体的实现步骤如下： 1. 定义一个数组 bit，长度为 n+1，用来存储树状数组。 2. 定义两个函数：lowbit(x) 和 update(x, v)。 lowbit(x) 函数可以返回 x 的二进制...
高级数据结构：树状数组详解（c++实现 求解动态数组区间和问题）
ylh的博客
01-24 2170
什么是树状数组？？？解决数据压缩里的累积频率（Cumulative Frequency）的计算问题，现多用于高效计算数列的前缀和， 区间和，这样的问题可以使用树状数组算法来解决。我们现在通过修改数组，往数组中某一个位置增加或减小一个值，从而导致前缀和数组会发生变化，因此我们不可以使用普通前缀和这一思路来做。 考虑一下：我们求静态数组的前缀和时，如果我们使用暴力法，使用两个for循环来枚举子区间之和，从而得到静态数组的区间和，但是这一复杂度会达到O（N^2），因此使用普通的前缀和可以将复杂度达到O（N）。但是
[学习笔记] 树状数组区间加+区间求和
Log_x's Blog
11-05 768
记bi=ai−ai−1,ci=(i−1)×bibi=ai−ai−1,ci=(i−1)×bib_i = a_i - a_{i - 1}, c_i = (i - 1) \times b_i，则： ∑i=1nai∑i=1nai\sum_{i = 1}^n a_i=a1+a2+…+an=a1+a2+…+an= a_1 + a_2 + … + a_n=∑i=11bi+∑i=12bi+…+∑i=1nbi=...
树状数组 区间加 区间求和_【LeetCode 327】区间和的个数
weixin_39827315的博客
11-22 256
题目描述给定一个整数数组 ，返回区间和在 之间的个数，包含 和 。 区间和 表示在 中，位置从 到 的元素之和，包含 和 。示例1输入： nums = [-2,5,-1], lower = -2, upper = 2, 输出： 3 解释： 3个区间分别是: [0,0], [2,2], [0,2]，它们表示的和分别为: -2, -1, 2。题解最暴力的解法就是 枚举所有区间，然后判...
树状数组区间求和三种模型
mr_lee
08-05 8321
树状数组在区间求和问题上有大用，其三种复杂度都比线段树要低很多……有关区间求和的问题主要有以下三个模型（以下设A[1..N]为一个长为N的序列，初始值为全0）： （1）“改点求段”型，即对于序列A有以下操作： 【1】修改操作：将A[x]的值加上c； 【2】求
树状数组 区间加 区间求和_[力扣307] 线段树&树状数组
weixin_39576294的博客
11-23 326
题目链接307. 区域和检索 - 数组可修改题目描述给定一个整数数组 nums，求出数组从索引 i 到 j (i ≤ j) 范围内元素的总和，包含 i, j 两点。update(i, val) 函数可以通过将下标为 i 的数值更新为 val，从而对数列进行修改。说明:数组仅可以在 update 函数下进行修改。你可以假设 update 函数与 sumRange 函数的调用次数是均匀分布的。样...
树状数组，区间修改+区间求和
最新发布
nufu_cow的博客
06-17 348
树状数组区间修改加区间求和
poj 3468 树状数组解法(解决区间更新，区间求和)
08-11 5127
题意：给你一个数列，每次询问一个区间的和，或者每次将一个区间的所有元素都加上一个数 一 算法         树状数组天生用来动态维护数组前缀和，其特点是每次更新一个元素的值，查询只能查数组的前缀和， 但这个题目求的是某一区间的数组和，而且要支持批量更新某一区间内元素的值，怎么办呢？实际上， 还是可以把问题转化为求数组的前缀和。       首先，看更新操作
树状数组区间加法&区间求和操作
weixin_30875157的博客
04-01 186
树状数组区间加法&区间求和操作 一般的树状数组解决区间加&单点询问并不复杂 但是要解决区间求和。。。 我们假设原数组是\(\{a_i\}\)，差分数组\(\{d_i=a_i-a_{i-1}\}\) 所以，我们有式子 \[a_x=\sum_{i=1}^xd_i\] 现在的问题是区间和，也就是求 \[\sum_{i=1}^xa_i\] 如果把每个都拆成上面的形式，那么我们就有 \[An...
树状数组--区间求和
热门推荐
dengdefang的专栏
09-12 1万+
树状数组是一个查询和修改复杂度都为log(n)的数据结构，假设数组a[1..n]，那么查询a[1]+...+a[n]的时间是log(n)级别的。所以如果要解决“数组中的元素不断被修改，怎么才能快速地获取数组中连续m个数的和”这个问题的话，用树状数组就再好不过了 　　首先，什么是树状数组呢？树状数组就是用另外一个数组再保存当前数组的值，设树状数组为C[n]，那么有C[i] = a[i -
一维二维树状数组区间加与区间求和
老臣
08-15 1489
在一般的情况下，对于区间加与区间求和，我们一般使用线段树。 树状数组在一般情况下，只能够单点查询，修改。 但是我们可以通过差分做到区间加或者区间求和（一维） 我们对于一个区间l,r，要求他们的和a[l]….a[r]。 设b[i]表示相邻两点之间的差(b[i]=a[i]-a[i-1])，那么对于sum(a[l]..a[r]) 明显有sum(a[l]..a[r])=(b[1]+b[2]+….+
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值