使用函数求素数和_素数定理

序言

上篇文章梳理了 Dirichlet 定理的证明，干脆一鼓作气，把素数定理（PNT）的证明也厘清好了；如果说我来到这个世界上有什么心愿的话的，那么我最想知道的就是素数定理的证明。

素数定理

其中

表示不超过

的素数个数.

符号说明

对于复变量

，

、

分别为其实、虚部

证明思路

• 重要角色

伟大的 Tchebychev 引入了一个与素数定理相关，同时又是方便使用解析工具的函数，

这实际上是一个“特征函数”的拣择的结果，

我们对该和式进行合并同类项，也即是说，将具有相同系数

的项合并，这是易于计算的，因为

并且在求和的过程中，只有素数的参与，其余的项皆为 0，那么

而接下来只需要证明一个事实，素数定理就可以得到证明，那就是

命题 1

若成立

，则素数定理成立.

证明

只需证明下式即可，

实际上这个不等式的证明只需要非常粗糙的放缩就可以解决。先证明后一个不等号，

此处暗示了

成立的可能性。最后证明该结论的第二个部分，这里需要一点小的技巧，先固定

，于是

整理，

注意到一个平凡的事实

，放缩并且不等式两边同时除以

，

因为

具有任意性，由极限的保号性可得最终结论。

Q. E. D

证明

• 解析之路

好了，现在聚光灯全部笼罩在

的上空，因为它俨然是证明素数定理的重要角色。不过，想要借用解析工具似乎还是有一段距离，我们知道，Euler 恒等式或是 Riemann 的

函数迄今为止是对素数最好的解析描述了，如果能与之建立关系，则成功指日可待。不过这段“关系”真可谓“九曲回肠”——

，

等式两边同时对

求导，

终于看到一点希望了。为了行文流畅，以便对接下来的工作得到合理的解释，我终于在此处才引入了另一个重要的函数（实际上早该引入了），

它与

当然是有关系的，通过

可知

其中

此关系成立是显然的。于是有

下面只剩下

与

的关系了。如果我直接告诉你，你一定觉得我疯了——

命题 2

，

别急，其实证明反而很简单，我们先来说明一个积分。

引理 1

构造围道如下图

图 1

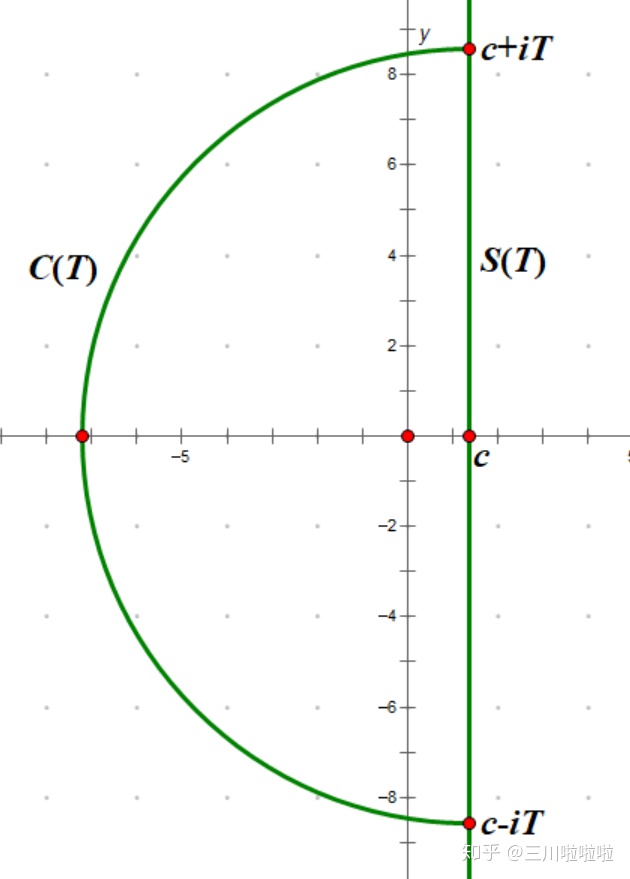
围道

由两部分构成，分别为

与

，沿逆时针方向为正方向。由留数公式可知：

其中

又因为

令

，等式右边第一项即为所求，而第二项趋于 0 ：

若

，

，又因为

，

所以

则可得

，

对于此种情况，依然可以做围道积分，只是围道半环分布在

的右侧，由于被积函数在该区域全纯，所以积分为 0.

Q. E. D

接下来我们就利用引理 1 可以证明命题 2 了。

证明

右

Q. E. D

得到了

的解析表达式，事实上命题就转换为——

命题 3

若

，则

，也就是素数定理成立.

证明

由于

是单调递增的，则有

我们看后一个不等式，

假如题设为真，则

蕴涵着

再由

的任意性，即可证明

；类似地，也可证明

，命题得证。

Q. E. Q

所有的的矛头指向了

以及它的解析表达式，

接下来的目标，就是我们将命题 2 中的积分项强行分离出主阶

，然后说明剩余的项都是低阶的。而素数定理的最难的部分也正是这里，因为它要求我们对

函数的性质要有更深入的理解。

• 技术核心

此节比较繁琐，建议先默认其中的结论，然后跳过阅读。等到大致思路搞清后，在会过来推敲其中细节。

函数在

的半平面内全纯，这是显而易见的事，而 Riemann 最非凡的创举是将 它解析延拓为复平面上的亚纯函数，并且

是它唯一的单极点。看看 Riemann 解析延拓的过程，就知道一流数学家的脑洞非同凡响——

命题 4

，

其中

，

证明

首先 Riemann 注意到了

与

两函数之间的关联

，

这显然是经过换元

得到的；我们发现等式右边出现了

，只需等式两边对

求和，右边即可得到

，而左边出现了

，因为

代入原式

Q. E. D

接着， Riemann 看到了

函数的对称性，

命题 5

是复平面上的亚纯函数，

与

是它的两个单极点，并且

证明

这个证明用到了关于

函数的恒等式：

它成立的依据是 Poisson 求和公式

而

带入求和即可得。如此一来，我们将该恒等式用到命题 4 当中，就会分离出极点。为了方便，记

由

恒等式可得

于是有

由此式立即可以验证

关于

的对称性，两个单极点也浮出水面，只不过需要验证后面的积分函数在

上全纯。关于这一点是肯定的，因为

（也就是

）是以指数型递减至无穷，

Q. E. D

如此一来，我们用

就可以研究

的解析性质就十分显然了。因为

已知

的 1 阶零点是

，而正好与

的单极点

约去，所以

唯一的单极点只是

；在而

附近

增长的性质的研究，对于后面证明素数定理所需要的估值至关重要。顺便说句题外话，对于

的非平凡零点（非负偶数点）， Riemann 认为它们分布在临界线

，这就是所谓的 Riemann 猜想。

命题 6

，

其中

在右半平面全纯。

证明

由微分中值定理，

，

于是

在右半平面一致收敛，令

Q. E. D

我们接下来可以使用该命题来展示几个重要的估值。

引理 2

，

，

，使得

（i）

，

且

(ii)

，

且

证明

（i）利用

之前提到过的两个估值：

由此可以放缩为

，

于是选取适当的

，应用命题 6，发现

(ii) 对于

的估值而言，利用 Cauchy 积分公式

只需令

，观察到积分圆在半平面

上，利用 (i) 即可得到 (ii)

Q. E. D

该定理反映了

在

被

控制着，对于任何一个

；即便在这根线的附近，其增长也是可控的。

命题 7

在

无零点

证明

我们需要先说明一个事实，最后由反证法得出矛盾。如果

，

，于是

这是因为

，代入右式有，

其中，

有了这个非负的论断，我们就可以在

（

）这个假设下，得到完全相反的结论，故完成命题 7。

因为

在

解析，于是该点至少为 1 阶零点，则

，

因为

是

的单极点，于是有

，

而

在

解析，于是在该点局部有界。综上三点，我们得出

，

其对数必为负，当

充分靠近 1 时，矛盾！

Q. E. D

然后是本节最后一个引理。

引理 3

，当

，

，则有

证明

由上一个定理论证，我们知道

，

变形，再由引理 2

接下来，考虑两种情况，

代入不等式继续放缩则得

将

替换为

即可满足引理；

我们选择较大的

来替换

，且满足

，于是由三角不等式

而后一项由中值定理来控制

于是由

别忘记我们的假设

选择系数

，于是得到

将

替换为

，证明完毕！

Q. E. D

• 最后一战

我们将要展现命题 3 的正确性，而它的证明需要两个事实作为支撑：

，

，

直观上讲，我们希望得到的阶是

，而被积函数中却是

，如果我们可以让

充分靠近

，并且达到该点，那么就达到我们的目的了，下面我们详细展开。

证明

固定

，与此同时也固定好

，我们记被积函数为

我们对原本竖直的积分路径（

至

）做一些变形为

，

图 2

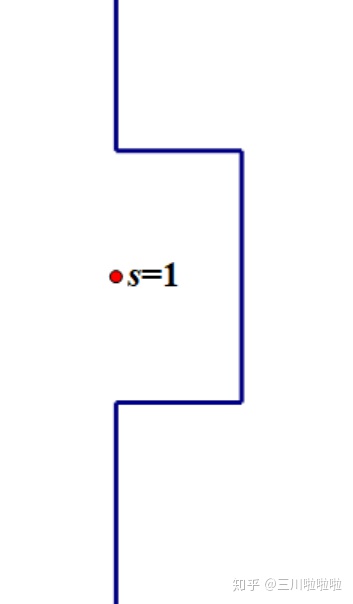
像通常利用 Cauchy 定理的方式一样，我们猜测

由引理 2、引理 3 这是成立的。固定任何

，当

，

于是积分在两个路径上收敛。

紧接着，考虑另一个积分路径

，选取足够小的

，使得

在下面的区域里无零点，

图 3

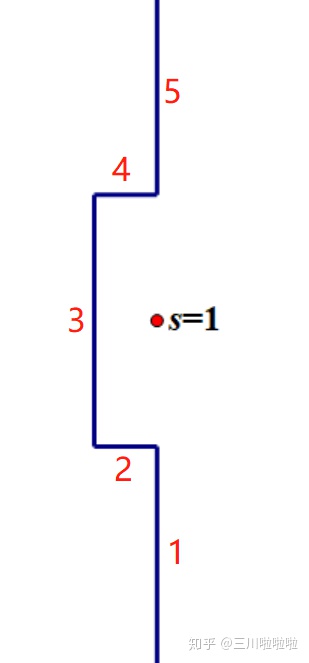
这是可以做到的，因为

在直线

上非零（命题 7）。

于是，

有一个单极点

，由引理 4，可知

在

的留数为

，即

图 4

接下来只需要对积分在

的积分进行逐段估值即可，分段标号如图 3。

• 与

当

充分大时，有结论

，

这是因为当

由引理 3 可知

，于是

由于此积分收敛，所以当

充分大时，可以任意小，于是不等号右边

；同理可得

的情况。

固定

，选择充分小的

，在

上时会有

又之前的引理可知存在

（依赖于

），满足

• 与

在这里，我们得到的结果是

同理。

终于来到最后一步估计，结合前面的所有转化和估计，即可完成证明，

即

Q. E. D

拔剑四顾心茫然……