ADF单位根检验三种形式_Toda-Yamamoto 格兰杰因果检验 TY-Granger方法

一、格兰杰因果关系定义

对于因变量，找到有助于预测的协变量。

"X is said to Granger-causeY if Y can be better predicted using the histories of bothX and Y than it can by using the history of Y alone."

二、格兰杰因果检验

格兰杰因果检验本质是对VAR模型的参数进行线性约束的检验（一般为检验系数是否为0），它使用Wald检验。Wald检验有效，建立在统计量服从渐进卡方分布的假设下。如果该假设被破坏，则Wald检验非有效，格兰杰检验也非有效。

那么在什么条件下假设会被破坏？比如某些变量是非平稳的；出现非线性约束时；预检验技术效力低...

在这之前，我们回到一般步骤：数据预检验+建模格兰杰检验

首先，数据预检验：单位根检验（ADF PP检验），协整检验（Johansen检验）

其次，建模和格兰杰检验：以下有三种情况

第一种情况：变量们都存在单位根（经济数据一般是一阶单位根，或者是在0~1之间的分数积整），且不存在协整关系，那么做一阶差分处理后，差分数据应用VAR建模，这样在对VAR系数进行检验时，传统渐进理论是有效的。

第二种情况：都存在单位根，存在协整关系，在水平数据（没有经过差分的数据）上应用ECM建模，再进行系数检验。

第三种情况：不管变量是否平稳，不管变量间是否存在协整关系，我们可以直接在水平数据上应用Wald检验来检验线性或非线性约束。这就是Toda Yamamoto 方法，简称TY-Granger方法。

TY方法保证了统计量服从渐进卡方分布，保证了格兰杰因果检验的有效性。

三、TY-granger方法步骤（E-Views）

1、单位根检验：确定积整阶数。尽量进行交叉检验。令变量中最大的积整阶数为m（一般m=1）。

单位根检验，只能一个一个变量地检验

2、确定最佳的VAR滞后阶数：

将所有变量划为1组，设定为group01.

这个使得构造VAR很方便

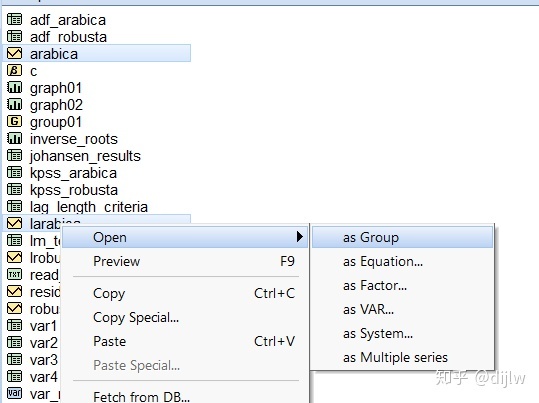
在原水平数据上进行VAR建模。滞后阶数设定为20（