两次结果的绝对差值_迈克尔逊-莫雷实验结果的再认识及其真实的物理意义

　　　　　　　　　　　作者：彭晓韬

[文章摘要]：本文试图通过对迈克尔逊-莫雷实验结果一种全新的解释来阐述光速不变假设的多余性，从而也进一步论述相对论的基础并不牢靠。

1887年，阿尔贝特·迈克尔逊和爱德华·莫雷在克里夫兰的卡思应用科学学校进行了非常著名的迈克尔逊-莫雷实验，目的是测量地球在以太中的速度(即以太风的速度)。但事与愿违，实验结果证明以太风的速度为0或根本不存在以太风。为解释此项实验结果与人们在实验前的预期完全不一致的问题，在1887年到1905年之间，许多著名的科学家提出了各种不同的解释。最著名者为荷兰物理学家亨得利克·罗洛兹，他依据相对于以太运动的物体的收缩和钟变慢的机制提出了后来以其名字命名的罗洛兹变换。然而，一位当时还不知名的瑞士专利局的小职员阿尔贝特·爱因斯坦，在1905年发表的一篇著名的论文中指出，只要人们愿意抛弃绝对时间观念的话，以太的观念就是多余的。但人们必须接受光速不变这样一个与人们所熟知的常理相违背的假设。这一实验自然就成了爱因斯坦相对论产生的重要背景。

为了解释本实验结果，是否必须放弃伽利略与牛顿的时空理论呢？我们不防对本实验作如下分析：

第一部分　早晚时分相向与背离运动时干涉条纹的相对变化

首先我们来分析利用早晨与傍晚时阳光相对于地球表面分别成相向与背离运动时对干涉条纹的影响：

一、在弹性碰撞理论条件下

如下图一《迈克尔逊-莫雷实验装置示意图》所示，当我们假设由光源Ｓ发出的光的速度为Ｃ，实验装置相对光源运动速度为Ｖ或-Ｖ时，则有：

1、按照伽利略-牛顿时空理论和速度叠加原理，入射到半透镜Ｍ的光速为：实验装置朝光源方向运动时，光相对与实验装置的运动速度为(Ｃ＋Ｖ)；而实验装置朝远离光源方向运动时，光相对与实验装置的运动速度为(Ｃ-Ｖ)；

2、如果我们把光子或电磁波束看成一种类似的弹性物质，当它遇到物体产生反射时，入射速度与反射速度相同；而遇到物体透射时，入射速度与透射速度也相同。那么，从Ｍ反射到Ｍ１并被Ｍ１反射回到Ｍ，再经过Ｍ透射到达目镜Ｔ的一路光的速度均与入射光速相同；同样地，从Ｍ透射到Ｍ２并被Ｍ２反射回到Ｍ，再经过Ｍ反射到达目镜Ｔ的另一路光的速度也与入射光速相同。

3、光程差和移动条纹数公式推导

　我们假设入射光波波长为λ；Ｍ与Ｍ１间距离为D；Ｍ与Ｍ２间距离为d；实验装置朝光源运动时的时差为Ｔ；实验装置远离光源运动时的时差为t；朝光源运动与远离光源运动间的时差为△t＝(t-T)；光程差为δ；移动条纹数为△N。则有：

Ｔ＝2D/(C＋V)-2d/ (C+V)=2(D-d)/(C+V) (式1)

t=2D/(C-V)-2d/(C-V)=2(D-d)/(C-V) (式2)

△t＝t - T =4 V (D-d) /(C2-V2) (式3)

将上式中的(D-d)简记为△d，则有：

△t＝4V△d /(C2-V2) 　　　 (式4)

δ＝Ｃ×△t＝4ＣV△d /(C2-V2) (式5)

△N＝δ/λ=4ＣV△d /[λ(C2-V2)] (式6)

4、迈克尔逊-莫雷实验理论计算

根据有关资料，迈克尔逊-莫雷实验所使用的实验观测装置的参数为：Ｄ＝ｄ＝11m。为了确保经分色后的阳光能产生干涉，Ｄ与d的差值△d应该很小，一般应该在数个或数十个光波长以内；利用的太阳光波长在可见光范围内，波长范围应为390～780nm范围内；利用太阳东升与西落时节地球表面相对于太阳成相反方向运动的速度差，在地球赤道上时的线速度最大，约为0.465m/s；空气中和真空中的光速分别为299600m/s和299792.5m/s。实验观测装置观测精度为0.01个干涉条纹间距。计算结果详见下表一：《光程差和移动条纹数理论计算表》。

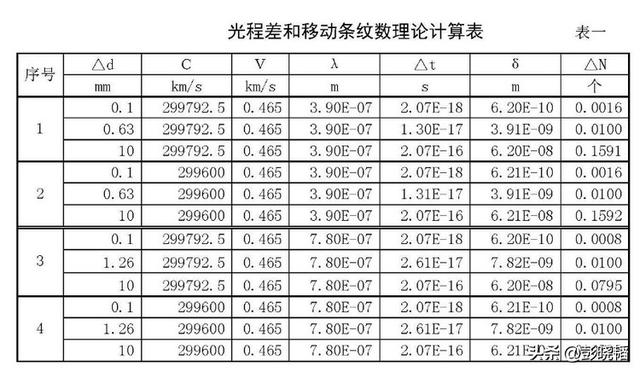
从上表中可以发现：当△d小于0.63mm(相当于807～1615个可见光波长)时，移动条纹数小于0.01个。也就是说，在此条件下，实验结果为：不能观察到干涉条纹移动。因此，若本实验中△d小于0.63mm的话，未观测到干涉条纹的移动完全正常，并不需要放弃伽利略和牛顿时空理论及速度叠加原理。

二、在以太存在的情况下

如果光波的运动的确与某种媒介有关(历史上假设的以太)，本实验是否真的能测量出地球与以太的相对运动速度呢？答案应该是否定的。原因如下：

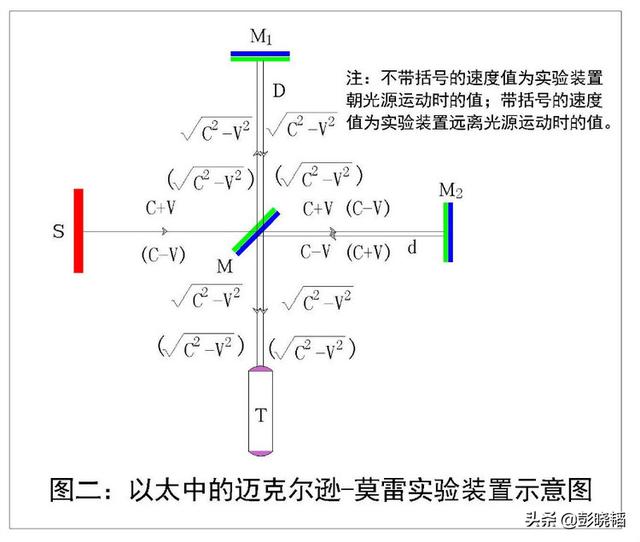
如上图二所示，并按上述第(一、3)款一样，我们假设入射光波波长为λ；Ｍ与Ｍ１间距离为D；Ｍ与Ｍ２间距离为d；实验装置朝光源运动时的时差为Ｔ；实验装置远离光源运动时的时差为t；朝光源运动与远离光源运动间的时差为△t＝(t-Ｔ)；光程差为δ；移动条纹数为△N。则有：

Ｔ＝2D/(C2-V2)0.5- [d /(C+V)+ d /(C-V)] (式7)

t=2D/(C2-V2)0.5- [d /(C-V)+ d /(C+V)]=T (式8)

△t＝T-t=0 　(式9)

δ＝0 　(式10)

△N＝0 (式11)

由上述推导可以发现，如果实验装置在朝光源与远离光源运动时的速度相同，则即使真的有以太的存在且光速在以太中的传播速度恒定不变，本实验也不能观测到地球与以太间的相对速度对干涉条纹的影响。

　第二部分　将实验装置旋转90度对干涉条纹的影响

在入射光波速度不变的条件下，对如图一所示的实验装置旋转90度前后干涉条纹变化情况如何呢？

一、在弹性理论条件下

首先，我们在实验装置旋转前，必须对实验装置进行调校，使由Ｍ1和Ｍ2反射回来的光产生干涉条纹。干涉条纹的亮区为光程差等于0或波长的整数倍；干涉条纹的暗区为光程差等于1/2波长或波长的整数倍加1/2。我们就以某一条暗纹为例(即光程差为(n+0.5)倍波长，n为整数，在本实验中其值应该较小)。则有：

实验装置旋转前光程差分别为：

实验装置朝光源运动时：

δ₁=(n+0.5)λ=[2D/(C+V)-2d/(C+V)]×C=2C(D-d)/(C+V) 　　　　(式12)

或者实验装置远离光源运动时：　

δ₂=(n+0.5)λ=[2D/(C-V)-2d/(C-V)]×C=2C(D-d)/(C-V) (式13)

实验装置旋转90度后，光程差分别为：

实验装置朝光源运动时：

δ_旋1=[2d/(C+V)-2D/(C+V)]×C=2C(d-D)/(C+V)＝-δ1=-(n+0.5)λ (式14)

或者实验装置远离光源运动时：　

δ_旋2=[2d/(C-V)-2D/(C-V)]×C=2C(d-D)/(C-V)＝-δ2=-(n+0.5)λ 　　(式15)

由(式14)和(式15)可知，旋转后的光程差与旋转前数值一样，只是正负相反而已。也就是说两路光到达目镜的先后顺序发生了逆转，但到达目镜的时差并未改变。因此，干涉条纹将不会发生变化。

二、在以太存在的情况下

同样地，我们在实验装置旋转前，必须对实验装置进行调校，使由Ｍ1和Ｍ2反射回来的光产生干涉条纹。干涉条纹的亮区为光程差等于0或波长的整数倍；干涉条纹的暗区为光程差等于1/2波长或波长的整数倍加1/2。我们仍以某一条暗纹为例(即光程差为(n+0.5)倍波长)。则有：

实验装置旋转前光程差为：

根据第一部分第二段论证，在以太存在条件下，实验装置朝光源运动和远离光源运动时的光程差相同，因此，我们只考虑实验装置朝光源运动情况就可以了：

δ=(n+0.5)λ=C×｛2D/(C2-V2)0.5- [d /(C+V)+ d /(C-V)]｝ (式16)

实验装置旋转90度后，光程差计算公式为：

δ旋=C×｛2d/(C2-V2) 0.5- [D/(C+V)+ D /(C-V)]｝ (式17)

当D=d时，(式16)和(式17)应该等价。因此，实验装置旋转90度后的光程差仍为(n+0.5)λ。干涉条纹不会发生变化。

当D≠d时，则根据(式16)可以推导出下式：

d=kD–(1/2)k2δ (式18)

式中k=(C2-V2) 0.5

将(式18)代入(式17)可得：

δ旋=2D(1-1/k2)-kδ 　 (式19)

　则有：

△δ＝δ旋-δ＝2D(1-1/k2)-(1+k)δ 　 (式20)

再将Ｄ＝11m、V=0.465km/s(有些资料中将此值定为30km/s，应是有误的，不应使用地球的轨道速度，应该用地球的自转速度。因为地球的轨道运动方向与太阳光方向存在90度的角度差)、Ｃ=299600km/s、δ=(n+0.5)λ代入(式20)可得：

△δ＝-5.29×10-11-1.99999999988 (n+0.5)λ (式21)

干涉条纹移动数目：

△Ｎ＝［(-5.29×10-11)/λ］-1.99999999988 (n+0.5) (式22)

下表二为可见光范围内，n可能数值(干涉光波列长度一般为10-8秒，因此，n值与光长相关，波长越长，最大n值越小)下的△δ和△Ｎ值。

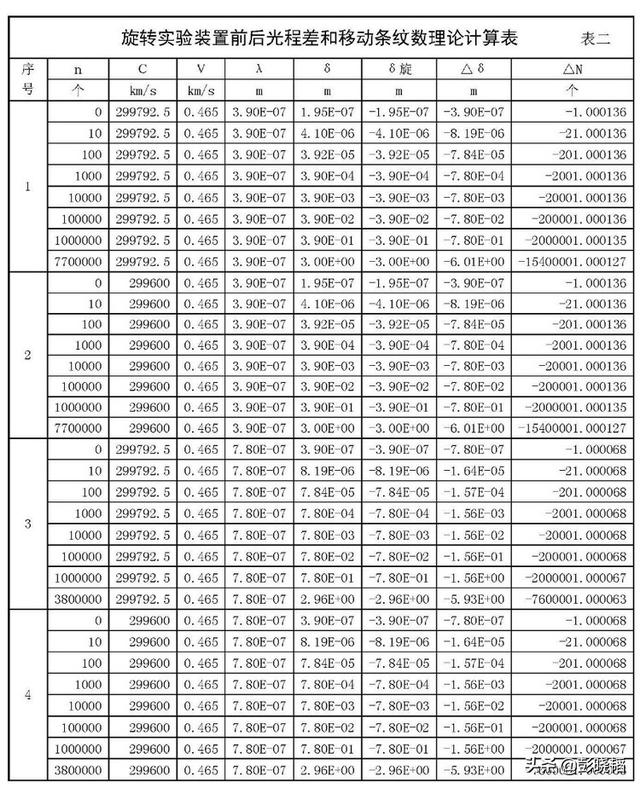
从表二可以发现：实验观测装置旋转前后光程差的确有变化，由原来的正值变为负值，且两者的差值的确为原来数值的两倍还稍多一点点。但同时也会发现：其整数倍数后的尾数很小，仅为波长的十万分之十四至七间，也就是说，干涉条件移动的绝对距离仅为0.00014～0.00007干涉条纹间距，而本实验装置的观测精度仅为0.01干涉条纹间距。因此，本实验未观测到干涉条纹移位完全符合理论计算。这也就是说，本实验结果并不能否定以太的存在。如果实验装置的观测精度能提高2个或2个以上数量级，即有观测到万分之七以上的干涉条纹移动的能力时，才有可能肯定或否定以太的存在。

综上所述，无论是用光具有的粒子性而可能符合弹性碰撞理论，或者以太真的存在但相对与地球表面的运动速度在0.465km/s以内时，本实验未检测到干涉条纹移动是正常的。并不能因此而否定以太的存在，更不能否定伽利略和牛顿的时空理论及速度叠加原理。同时，也没有必要假设光的传播速度不变。