“ 两个随机变量的联合概率分布、边缘概率分布和条件概率分布”
随机变量是定义在样本空间上的数值函数,在介绍离散随机变量和连续随机变量的时候,我们仅仅讨论样本空间上的一个随机变量。如果我们对样本空间的两种特性或变量感兴趣,那么就需要在样本空间上定义两个随机变量,这两个随机变量交集的概率分布称为二元概率分布。本文将带领你认识二元概率分布中的几个基本概念--联合概率分布、边缘概率分布和条件概率分布。
01
—
离散随机变量的二元概率分布
联合概率分布
假如我们对样本空间中的每个简单事件指定两个数,一个对应于离散随机变量X,另一个对应离散随机变量Y,那么每一个简单事件将对应两个数值事件(X的取值和Y的取值)。
用字母A表示数值事件X,用字母B表示数值事件Y,则两个数值事件交集的概率可表示为:
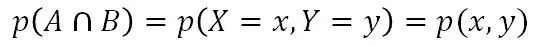
能够给出所有X和Y取值的每一个组合(x,y)概率的图、表、公式称作X和Y的联合概率分布(二元概率分布)。根据事件的交的运算法则,可得联合概率分布的计算公式:
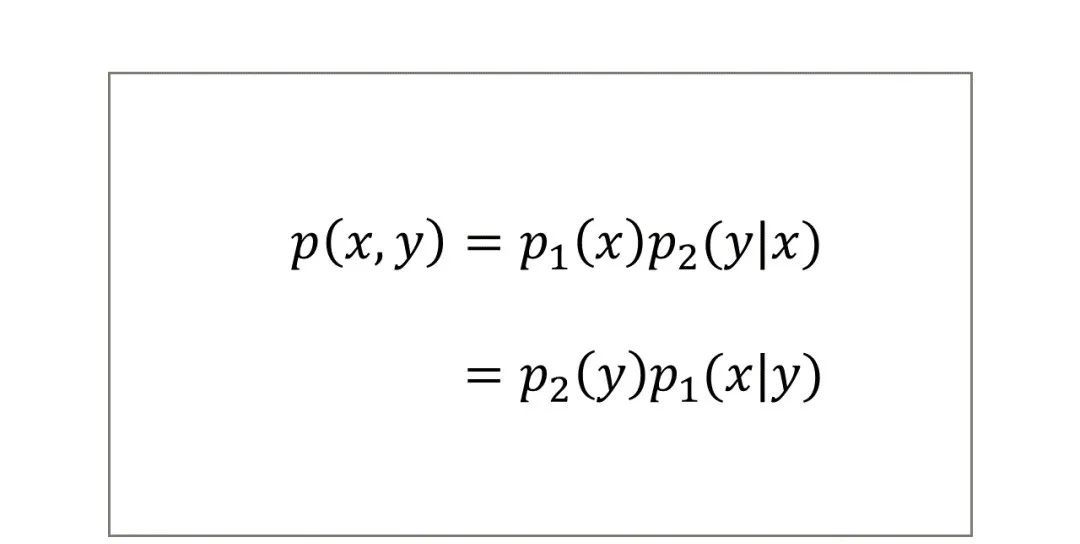
其中,p1(x)和p2(y)分别是X和Y的边缘概率分布,p1(x|y)和p2(y|x)分别是X和Y的条件概率分布,详见下文。
联合概率分布具有如下性质:
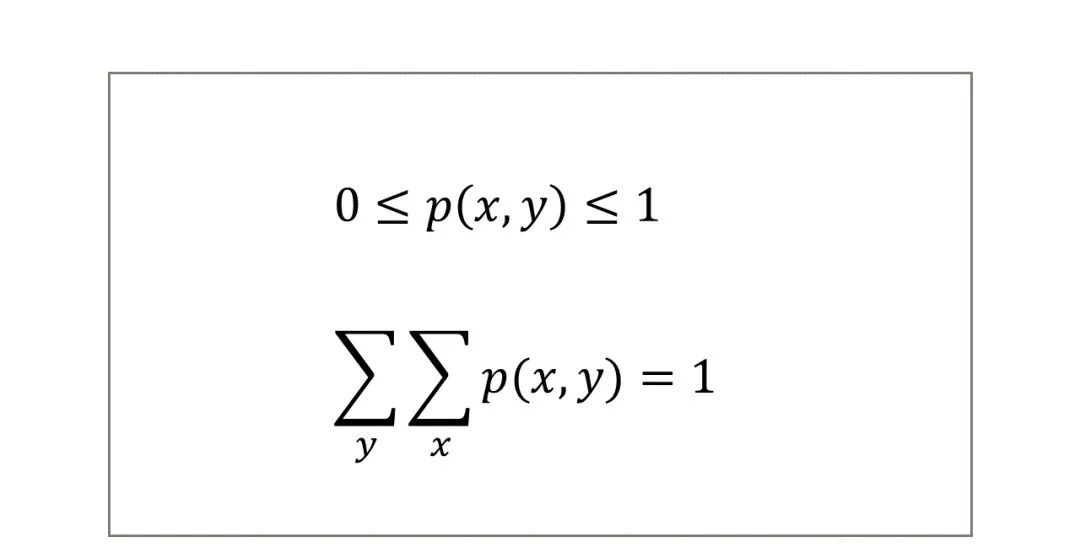
边缘概率分布
如果样本空间上被定义了两个随机变量X和Y,但是我们仅仅对X的观测值感兴趣,或者只对Y的观测值感兴趣,给出X所有取值的概率的图、表、公式称为X的边缘概率分布;同样地,给出Y所有取值的概率的图、表、公式称为Y的边缘概率分布。
为了方便起见,当提及X的概率分布时,使用下标1,提及Y的概率分布时,使用下标2。假设p(x,y)是X和Y的联合概率分布,则X和Y的边缘概率分布的计算公式如下所示:

边缘概率分布具有如下性质(以X的边缘概率分布为例):
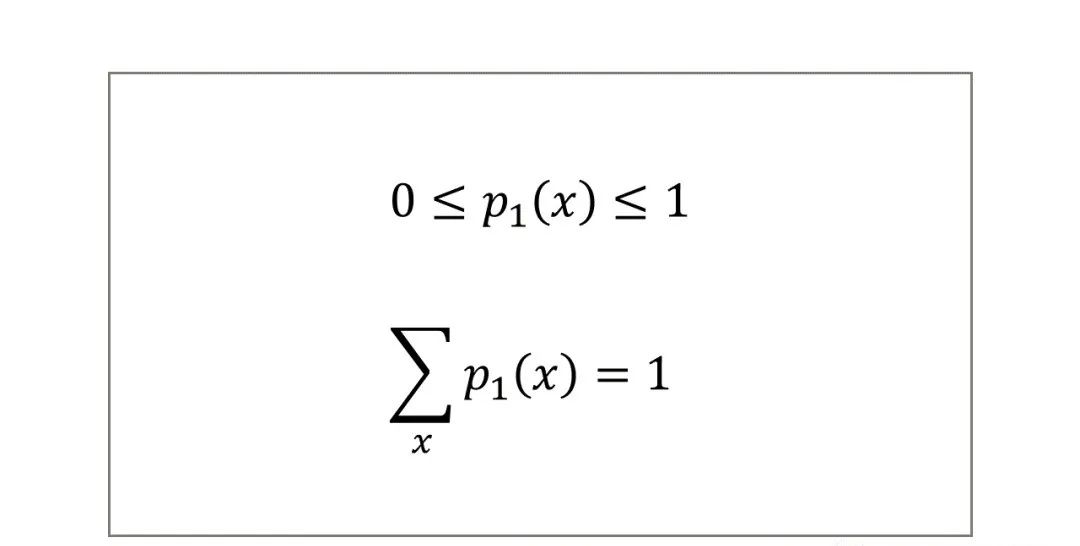
条件概率分布
在给定Y=y的条件下,发生数值事件X=x的概率是事件Y=y下X=x发生的条件概率。能够给出所有Y取值下所有X取值的条件概率的图、表、公式称为给定Y时X的条件概率分布。
假设p(x,y)是X和Y的联合概率分布,p1(x)和p2(y)分别是X和Y的边缘概率分布,则条件概率分布的计算公式如下所示:

条件概率分布具有如下性质(以给定Y时X的条件概率分布为例):
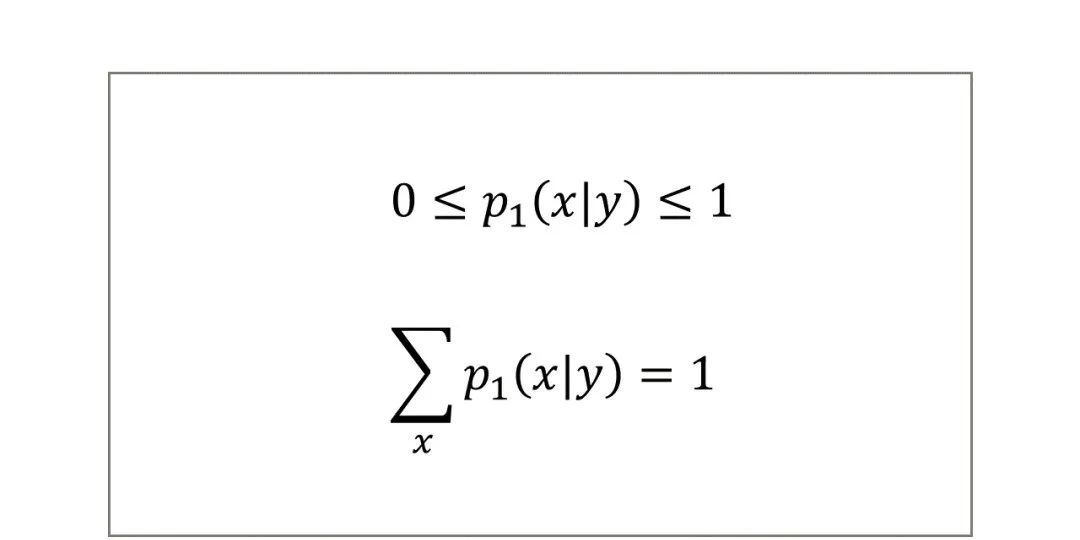
02
—
连续随机变量的二元概率分布
联合概率密度函数
离散随机变量的二元概率分布中的定义也适用于连续随机变量,不同之处在于离散随机变量的概率是求和,而连续随机变量的概率是求积分。
与离散随机变量的联合概率分布类似,连续随机变量X和Y的联合概率密度函数f(x,y)的计算公式如下所示:
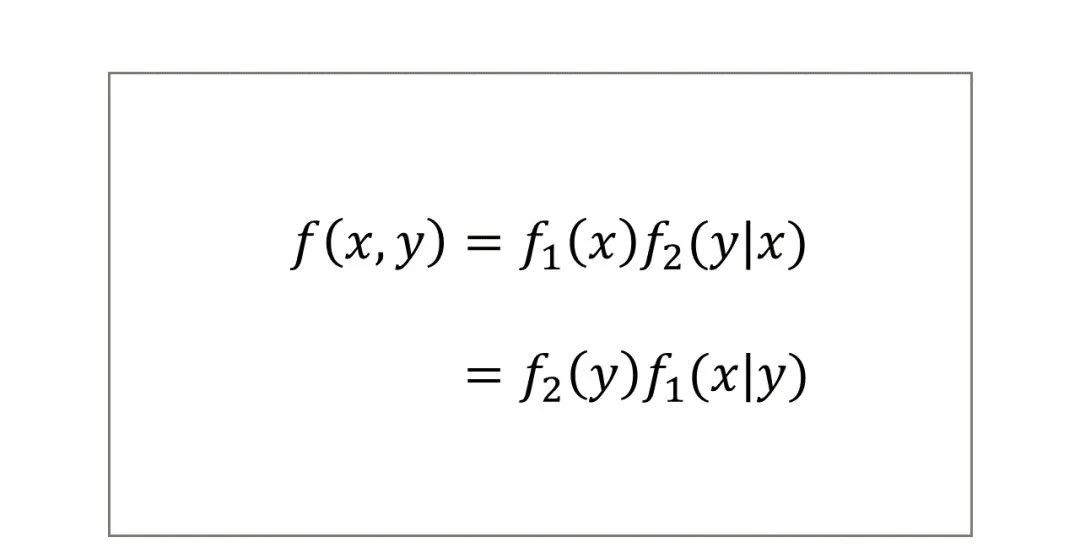
其中,f1(x)和f2(y)分别是X和Y的边缘概率密度函数,f1(x|y)和f2(y|x)分别是X和Y的条件概率密度函数,详见下文。
联合概率密度函数具有如下性质:
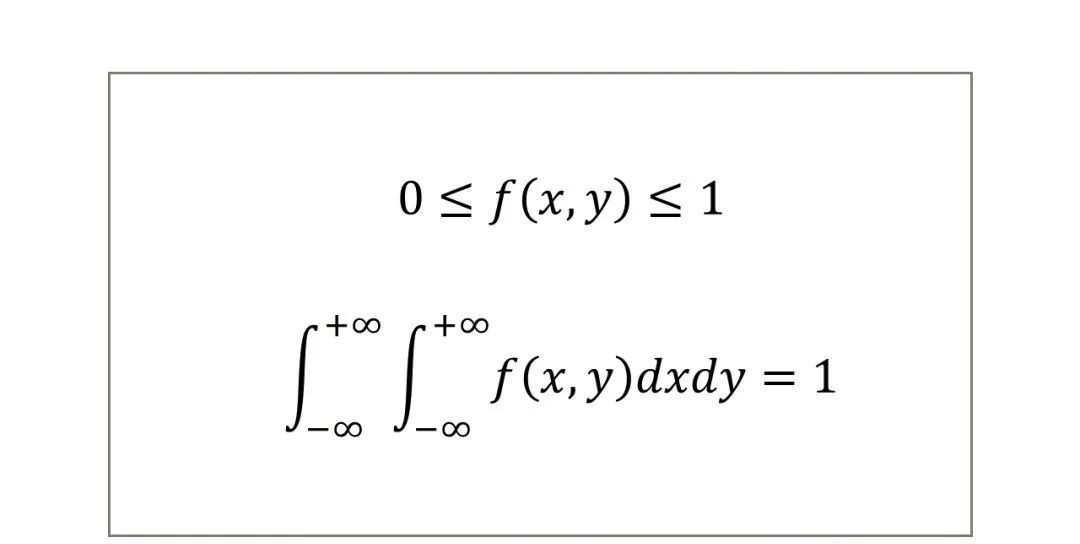
边缘概率密度函数
假设f(x,y)是连续随机变量X和Y的联合概率密度函数,则X和Y的边缘概率密度函数分别为:

边缘概率密度函数具有如下性质(以X的边缘概率密度函数为例):
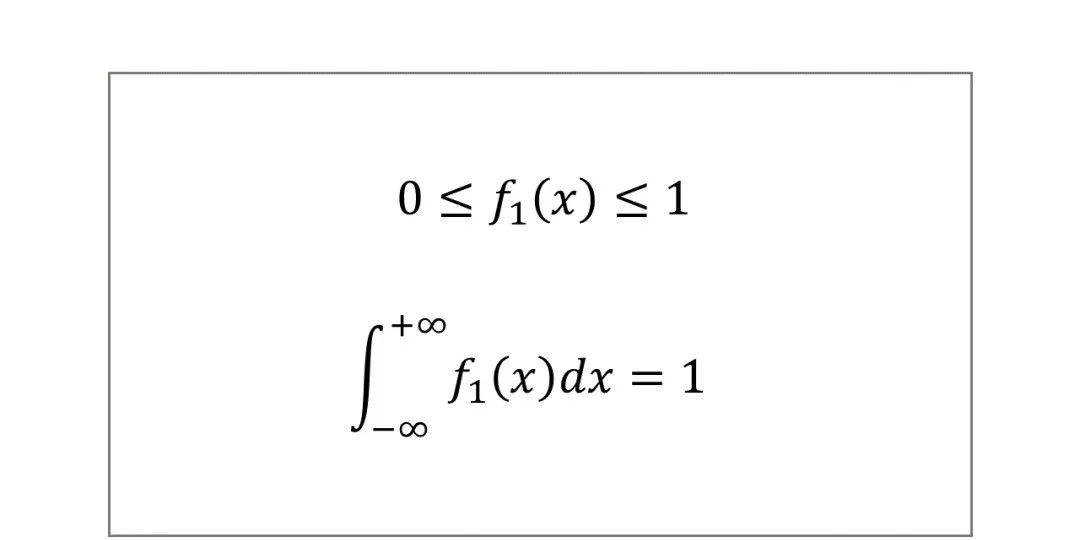
条件概率密度函数
假设f(x,y)是连续随机变量X和Y的联合概率密度函数,则X和Y的条件概率密度函数分别为:

同样,条件概率密度函数具有如下性质(以给定Y时X的条件概率密度函数为例):
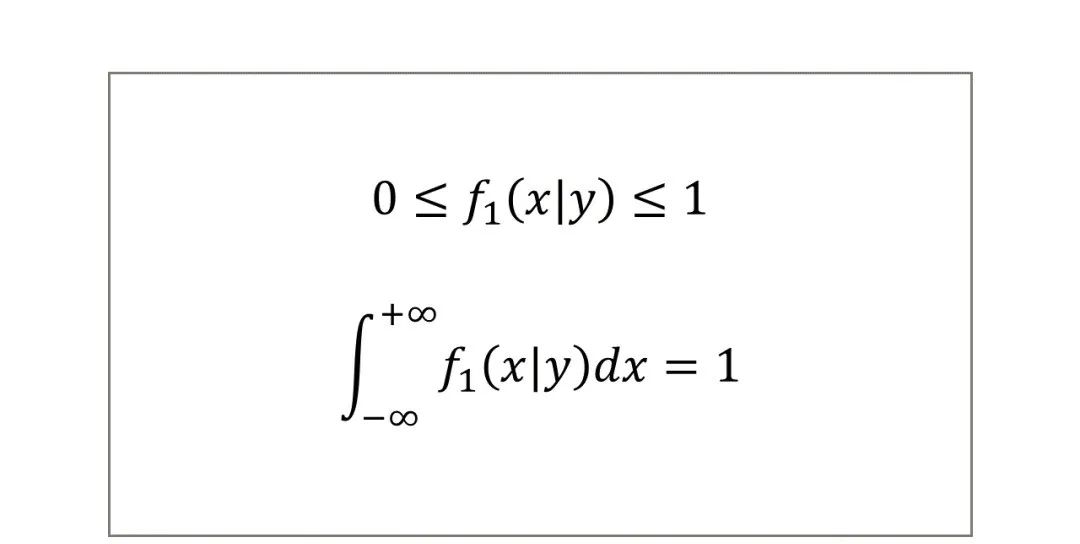
03
—
应用举例
离散随机变量的二元概率分布
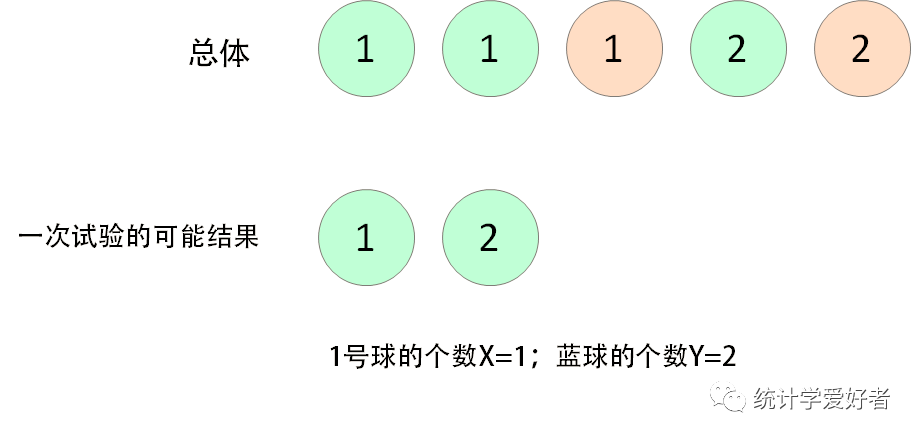
如下图所示,从总体中随机抽取2个球,令X表示抽出1号球的个数,令Y表示抽出蓝球的个数,求X和Y的联合概率分布、边缘概率分布和条件概率分布。
解:
1)联合概率分布
1号球个数X的可能取值为0、1、2,蓝球个数Y的可能取值也是0、1、2,因此一共有9种组合的(x,y)。从5个球中抽取出2个球的可能方法有5!/(2!*3!)=10种,根据简单事件的计数法则,易得X和Y的联合概率分布:

即p(0,1)=1/10,p(1,0)=1/10,p(1,1)=3/10,p(1,2)=2/10,p(2,1)=2/10,p(2,2)=1/10;
2)边缘概率分布
根据边缘概率分布的计算式,易得X和Y的边缘概率分布:

即X的边缘概率分布为p1(0)=1/10,p1(1)=6/10,p1(2)=3/10;Y的边缘概率分布为p2(0)=1/10,p2(1)=6/10,p2(2)=3/10;
3)条件概率分布
根据公式可知,条件概率分布等于联合概率分布除以边缘概率分布,例如p1(0|1)=p(0,1)/p2(1)=1/6,如下图所示:

因此,给定Y时X的条件概率分布为:
p1(0|0)=0,p1(1|0)=1,p1(2|0)=0;
p1(0|1)=1/6,p1(1|1)=1/2,p1(2|1)=1/3;
p1(0|2)=0,p1(1|2)=2/3,p1(2|2)=1/3;
给定X时Y的条件概率分布为:
p2(0|0)=0,p2(1|0)=1,p2(2|0)=0;
p2(0|1)=1/6,p2(1|1)=1/2,p2(2|1)=1/3;
p2(0|2)=0,p2(1|2)=2/3,p2(2|2)=1/3;
连续随机变量的二元概率分布
假设连续随机变量X和Y的联合概率密度函数为:
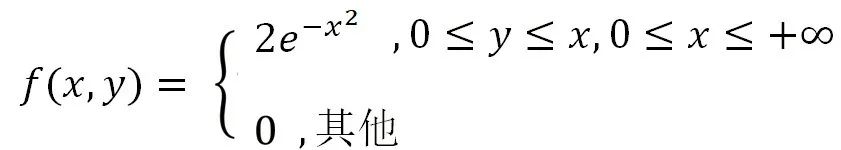
求边缘概率密度函数f1(x),以及条件概率密度函数f2(y|x)。
解:
1)边缘概率密度函数
X的边缘概率密度函数为:
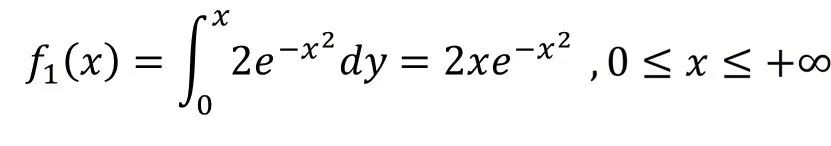
2)条件概率密度函数
给定X时Y的条件概率密度函数为:
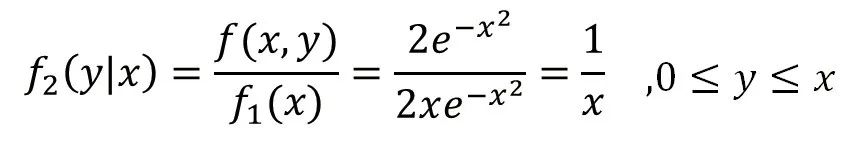






 本文详细介绍了二元概率分布的概念,包括离散随机变量和连续随机变量的情况。通过实例解析了联合概率分布、边缘概率分布和条件概率分布的计算与性质,并提供了具体的计算公式。此外,还探讨了在实际问题中如何应用这些概率分布。
本文详细介绍了二元概率分布的概念,包括离散随机变量和连续随机变量的情况。通过实例解析了联合概率分布、边缘概率分布和条件概率分布的计算与性质,并提供了具体的计算公式。此外,还探讨了在实际问题中如何应用这些概率分布。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








