前言:受好友邀请在专栏写一点文章,最近正好因为某些原因在看魔方与群论的数学知识,于是准备写这么一篇。本人非常喜欢群论,群论入门其实非常简单,但其本身又非常迷人。大一一年里我倒是因为机缘巧合学了不少群论 ,看了A.ZEE的<Group theory in a nutshell for physics>,《代数方程与置换群》,《对称和群》等一些小书(但其实都忘得差不多了5555)。群论与数学,理论物理,化学都密切相关,足见其重要性。
相信很多人都知道魔方与群论密切相关,但具体是怎么一回事可能就不太了解了。关于魔方的解法,据我所知很多人都是背公式,但我个人觉得如果只是看公式那么魔方就变成了一个手速游戏,个人认为这样失去了很多趣味性(很自豪地说我初中自己总结出了还原魔方的公式,后面每次忘记都能重新发明,于是至今也没有背过流行的公式,不过自己的公式比现行的公式复杂度高很多倒是真的)。
本文主要参考<Group Theory via Rubik's Cube>,链接:http://geometer.org/rubik/group.pdf
如果手边有一个魔方最好,如果没有,网上有一个魔方的模拟程序,可以走特定步数,一键还原,甚至可以统计方块的移动情况。(只不过windows 版本有些显示问题,因为软件比较老了,很可能不能正常使用)链接:Rubik Downloads
一、准备工作
我们先介绍一些有关魔方的基础信息。
魔方有三种不同的方块,分别为角块(8个,每个角块有三种颜色),棱块(12个,每个棱块有两种颜色)与中心块/面心(6个,每个中心块有一种颜色)。魔方总共有6个面,也就是6种颜色,每种颜色被分为九个小面,我们称之为facelets,也就是魔方总共有54个facelets。
我们操作魔方的时候,常常将面心的位置固定,将一个颜色的面心对准自己,同时也固定其上下左右的面心颜色,不再转动。于是魔方被分为6个方位,上(UP),下(DOWN),左(LEFT),右(RIGHT),前(FRONT),和后(BACK)。我们转动魔方时用字母代替操作,取每个面的首字母代表将该面对准自己后顺时针转动这个面90°。
例如,F就是将对准自己的面瞬时针旋转90°,R就是将右边的面心对准自己后旋转90°(注意操作中的“将该面对准自己”只是个假想操作,为了方便你了解转动魔方的方向),同理,B就是从目前的视角看,逆时针旋转离你视角最远的面心所在面90°。
那么转动两次即:
注意魔方的旋转操作是非交换(非阿贝尔)的,例如FR≠RF,因此逆操作的顺序也要特别注意,比如FR的逆为rf而非fr,自己可以尝试尝试。用字母表示则为:
二、一些基础知识
操作的阶(order):
我们容易知道,对于一个还原的魔方,做任意一个固定的操作组合(macro),重复有限次后魔方必定重新被还原。那么对于这个重复的次数,我们就叫做一个操作的“阶”。
例如,操作F的阶为4,而(FFRR)的阶为6,而操作组(FFLLBR)的阶为90。用开始给出的应用程序可以计算某操作组的阶数。
现在我们来证明任意一个操作组进行有限次后,魔方必定会被还原成原来的状态:
我们把这个操作叫做P,重复P的次数用次方的记号表示。显然不进行任何操作即
由于每重复一次P魔方的状态都会被重排一次,而魔方的状态数是有限的,因此在不断重排中必定存在两个相同的状态。设操作P进行k次后达到某状态,P进行m次后再次达到该状态,即
若k=0,那么得证。如果k≠0,那么
所以任意一个操作组进行有限次后,魔方必定会被还原成原来的状态。
由此,我们可以借助程序或者手动观察任意操作组的阶数。
有趣的是,操作(FFRR)的阶数为6,而6有因子2和3,而将操作(FFRR)重复两次或三次能获得比较规整的结果,但重复别的次数,比如五次,会获得比较乱的结果。同理,阶数为90的操作(FFLLBR)有因子45,将此操作重复45次也能获得比较有趣的结果。对于阶数较高的操作可由上文提到的程序实现。这一操作和置换群的性质有关。
三、群
什么是群?
群是一个包含有特定元素的集合,且在群元素上定义了一个二元运算*(例如乘法,加法),满足以下四个条件:
1、运算*是闭合的。也就是如果g,h是群G中的两个元素,那么g*h也是群G中的元素。
2、运算*符合结合律。也就是说(f*g)*h=f*(g*h)
3、群G中有单位元e。也就是说e*g=g*e=g。
4、群G中的每一个元素,对于运算*存在逆元。也就是说,任意g∈G,存在
以下有几个注意点:
1、群元素不一定是数字或矩阵,可以是任何抽象的东西,比如三维空间中的旋转,某种抽象的置换等等。
2、二元运算*不是乘法。是某种抽象运算的意思。具体含义因群而异。
3、运算*不一定符合交换律。也就是g*h不一定等于h*g。如果这个运算对于每个元素都符合交换律,那么该群称为交换群(阿贝尔群),如果该运算对于某两个元素不符合交换律,那么该群称为非交换群(非阿贝尔群)。
4、上述四条条件中,关于单位元和逆元的部分可以去掉一半。也就是说,只需要左单位元和左逆,群的定义依然不会改变。即通过e*g=g和
5、为了方便,我们可以省去*的记号。例如
6、群元素可以是有限的,也可以是无限的。比如平凡群只有一个元素,那就是单位元。有两个元素的群比如{-1,1}配上“乘法”这个二元运算。而整数在加法下也是一个群,其中有无限个群元素,其单位元是0。有理数除去0在乘法下也是一个群,其单位元是1。
四、一些群的例子
比较简单的例子上文我已经提过了。比如整数在加法下形成的群,±1在乘法下也构成群。
一些别的例子:
exampli gratia:n次单位根在乘法下形成一个有n个元素的循环群。记为
克莱因四元群:是两个Z2群的直和:

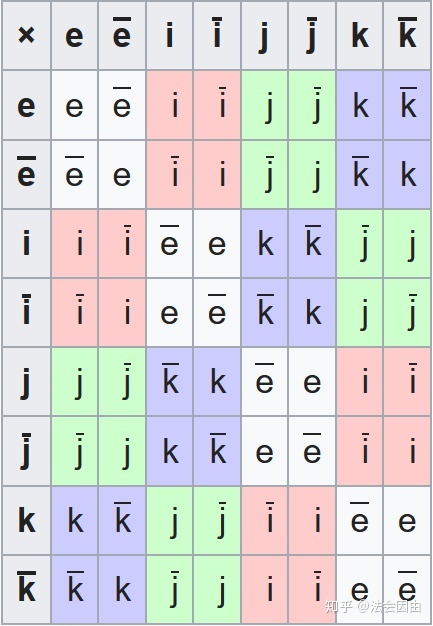
四元数群Q(有八个元素):{1,-1,i,j,k,-i,-j,-k},运算法则为:
正多边形的对称群
旋转群:如果我们把空间中的旋转作为群元素,而运算则是旋转之间的叠加,那么我们可以获得旋转群。对于二维空间,我们有群:SO(2)也就是special orthogonal group,大家可以自行了解旋转矩阵。S代表矩阵的行列式为1, O代表正交,也就是群元素正交:
然后是我们的主角:置换群!魔方群其实是一个置换群的子群。
五、置换群
我们首先得了解什么是置换:
所谓置换,就是将一系列有顺序的元素重新排列。比如数字1,2,3,4我们可以将其重新排列,例如重新排列成1,3,2,4,也就是2和3换了位置。其实质是2和3换了位置,至于名字叫什么都是无关紧要的,无论是叫1,2,3,4还是叫A,B,C,D,只要置换的实质没变,那么这个置换就是一样的。
我们可以把置换表示成以下形式:
为了方便起见,我们的置换可以被标记成另外一种形式,也就是所谓的cycle notation:
我们知道,上面这个置换其实就是把2和3换了位置,而1和4位置不变。
那么我们可以把这个置换表示成,(1)(4)(2 3),表示1和4位置不变,而2变成3,3变成2。
我们来看下面这个置换:
那么两个置换的复合运算呢?比如先进行(1 4),再进行(1,3)我们会得到什么?
在有些书中,关于置换的复合是从右往左进行的,比如先进行(1 4),再进行(1,3)我们把它写成(1 3)(1 4)(比如A.ZEE的群论),而有的书中则写成(1 4)(1 3)(比如笔者写本文所参考的魔方群的文献),因为本文写的主要有关魔方,那么我们遵循从左到右的运算顺序。(1 4)(1 3)意味着1投入了4的盒子,4先投入了1的盒子然后再转移到3的盒子,最后3被投到1的盒子里。也就是(1 4)(1 3)=(1 4 3)。但是,如果把(1 4)(1 3)从右到左运算的话,我们会得到(1 3 4)。可见两个置换的运算顺序是不可以交换的。
我们把置换括号内的数字个数成为置换的阶,比如(1 4)是二阶的置换,而(1 3 4)是三阶的置换。如果我们把(1 4),也就是一个二阶的置换重复两次,我们会得到什么?我们先把1 投到4的盒子里,然后再把它投回1的盒子里。所以1没有改变位置。同理,4也没有改变位置。那么
也就是证明
那么我们的置换群也就新鲜出炉啦!我们可以把给定n个元素的置换当成元素构成一个群,运算法则就是置换的复合。
比如我们把三个元素的置换构成一个群
奇置换与偶置换
由上面的习题我们可以知道,任何一个置换都可以表示成多个二阶置换的复合,即
那么因此,多个置换复合也可以表示成多个二阶置换的复合
我们把任意一个置换分解成二阶置换后,如果二阶置换有奇数个,那么我们称这个置换为奇置换,反之则为偶置换。
习题(有点点难度,且与本文关系不大,可跳过):
对于集合
限于篇幅,本文先介绍到这里,后面会接着出新的部分。内容包括,魔方群究竟是什么,有多少个元素,如何利用交换子发明魔方公式,如何利用降群法解魔方等内容。
第二篇:
法会因由:魔方与群论(二)(交换子牛啤!)zhuanlan.zhihu.com
第三篇:
法会因由:魔方与群论(三)(人类使用交换子,神仙减少生成元)zhuanlan.zhihu.com























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








