三阶矩阵的lu分解详细步骤_<读书笔记6>稀疏矩阵Cholesky分解[1]

本篇为稀疏矩阵求解算法经典论著<Direct Methods for Sparse Linear System>的<读书笔记 6>

稀疏矩阵的消去树（Elimination tree）部分，在书中的第4章Cholesky分解的第一节。消去树甚至要比稀疏三角方程求解更为重要，他出现在很多算法以及定理中。引入消去树的目的在于减少计算图的可到达性。

4.1 Elimination tree

首先我们先从Cholesky分解入手，对于一个稀疏对称正定矩阵

可以分解为

,其中

为下三角矩阵，并且对角线元素为正值。在矩阵

中出现的非零entry，如果没有在矩阵A中同样的位置非零，这被称为fill-in，即矩阵

的非零样式中新填入了非零entry。我们令图

为矩阵

的无向图，这个图被称为 矩阵

的 filled graph。

Fill-in会对稀疏矩阵带来非常多的麻烦，所以一般均要通过符号分析（symbolic analysis）获取

的非零样式。分析的步骤包括了消去树（

elimination tree），计算消去树的后根次序（postordering），以及计算

的每一列的非零样式（即计算column counts）等等。

现在我们利用稀疏三角方程

作为基础，来实现

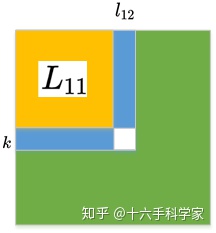
up-looking Cholesky分解。同样对

也做2*2的块分解。

从而得到三个方程：

;

;

第一个方程为递归求解；第二个方程为一个三角方程组求得

；第三个方程化简为

。从而看到每一次递归，可以依次从上向下求出矩阵

的行。并且可以看出，每一行的非零样式，是由第二个三角方程组可以得到的。可以参见：

十六手科学家：<读书笔记5>稀疏矩阵解三角方程组​zhuanlan.zhihu.com

其伪代码为

---

好的，那么现在正式来介绍消去树。考虑到上面的三个方程中的

，向量

的转置即为

的第

行。所以他的非零样式

，其中

是

的有向图，

表示

的第

行的非零样式，

表示了矩阵

的第

列的上三角部分的非零样式。

那么如果得到

？通过对

深度优先搜索DFS可以实现。但是存在更简单的方法，仅需要耗时

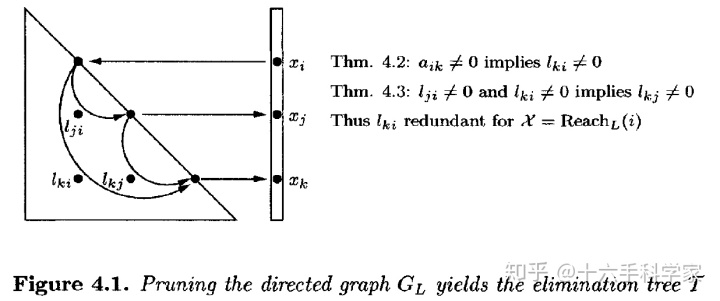
。此处依赖两个定理：

定理4.2，对于Cholesky分解

，如果

,则有

。

定理4.3，对于Cholesky分解

，如果

,则有

。

如上图所示，首先对于

，由定理4.2，保留了所有原始矩阵

的非零特性，在图中以实心圆表示。然后观察第一列

与

非零，所以由定理4.3在

中

非零，由

表示。然后再同理处理第二列，第三列......知道最后一列。即得到上图中的

非零样式。此时即完成了

符号分析。

那么如何得到消去树呢?

首先，可以通过对

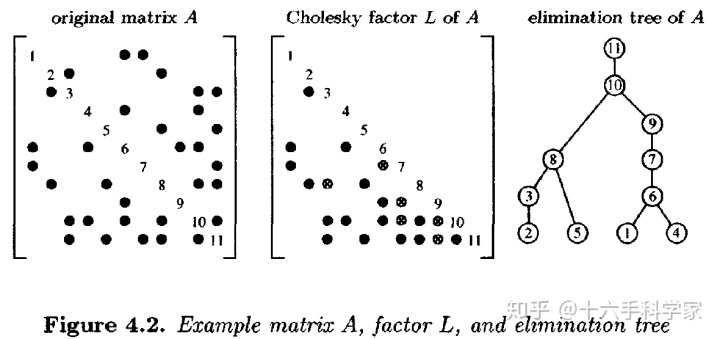
的有向图，然后通过广度优先搜索（BFS）得到消去树。即依次对节点1至n，取距离当前搜索节点i最近的节点j作为parent，没有parent的节点作为tree的根。例如在图4.2的矩阵所对应的graph如下图，node(1)的在node(6,7)中取node(6)为父节点；node(2)在node(3,8)中取节点node(3)为父节点，node(3)在node(8,9,10)中取node(8)为父节点......从而构成了如上图的消去树。

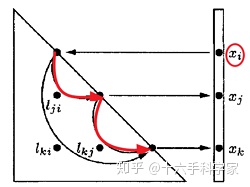
另外一种更为简单的方法。仍然见图4.1，因为存在一个path从

到

,并且经过

。所以在计算

的时候，并不需要遍历

。即如下图所示，仅需要按照红色path遍历，而经过

的黑色path是冗余的，不再需要遍历。从而对于任意节点

, 如果

从图中移除，对于

，同样不会影响path

。意味着移除这样的边，仅留下从节点

出发的最外层的边，并不会影响

。

即如果

为大于

的并且满足

的最近的节点，则对于所有

，非零的

都是冗余的。

这样的结果就是消去树。tree中节点

的父结点是

，

为第

列中从

到

的第一个非对角非零entry的行索引，(即

)，如果第

列没有非对角非零项，节点

是树的根，它没有父结点。实际上消去树应该为forest，因为可能会有多个根，但是为了简便表达，就统一称之为tree。假设treed的edge是从child到parent的有向的。这里用

表示

的消去树。并且用

表示 即

的前

行与前

列构成的子矩阵

的消去树。

同样例如图4.2中的矩阵，第一列中，

与

非零，则取

所在行为6，所以node(1)的parent为node(6)；第二列，

与

非零，则取

所在行为3，所以node(2)的parent为node(3).......知道最后一列。

证明了消去树的存在性;现在有必要计算它。还需要几个定理。

定理4.4 ：对于Cholesky分解

，如果

,并且

,意味着在消去树

中，

是

的descendant，等价于

是

中的一个path。

定理4.5：

的第

行的非零样式

由下式得到：

。

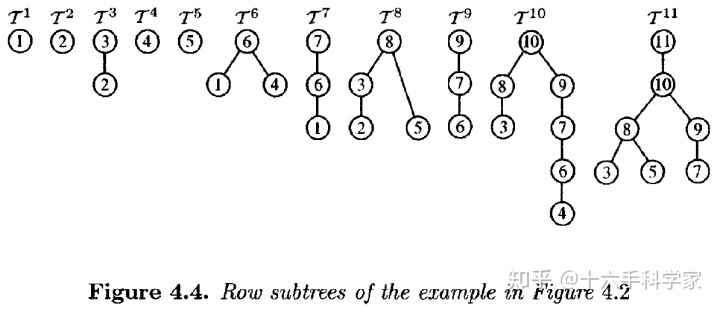
通过定理4.5可知，对于第

行的subtree

，是

的subtree。下图中为图4.2矩阵中的subtree。

定理4.6：对于消去树

中，

的每个descendant

。当且仅当

并且

,则节点

是

的一个叶。

推论4.7：对于Cholesky分解

，如果

,并且

,意味着在消去树

中，

是

的descendant，等价于

是

中的一个path。

定理4.4和推论4.7引出了一种算法，它在几乎

时间内得到消除树

。如果

已知，并且可知它为

的subtree。通过

计算

，

的children是一定能找到的（为

的root node）。由

推导出path

存在于

中，这条path在

中遍历直到达到跟节点。这个节点一定是

的child，原因是

是一定存在的。

cs_etree函数计算

的Cholesky分解的消除树(假设ata为False)。

如果cs_etree函数输入参数ata为真，则为在不形成

的情况下计算

的消除树。这是列消去树（

column elimination tree）。它将用于QR和LU因子分解算法。

函数	功能
int *cs_etree (const cs *A, int ata)	计算消去树用于Cholesky或者列消去树用于QR以及LU分解
int *cs_idone (int *p, cs *C, void *w, int ok)	返回一个int数组并释放workspace