求给定精度的简单交错序列部分和_单个神经元的简单模型：Leaky integrate and fire (LIF) model...

神经元的交流，传输与活动，都离不开一个个非常短暂的脉冲-Spike。有各种各样的模型，可以描述神经元的电位变化，发放，比如HH模型等等。但是如果只考虑比较粗糙的一些性质，比如膜电位的简单变化和spike的频率之类，可以直接利用神经元的膜电位性质（与电容类似），以及其动作电位这种比较模式化(stereotypical)，又比较短暂的性质，吧神经元抽象为一个电容，以及超过特定阈值会产生一个大的spike，且有一定的不应期(Refractory Period)的简单模型。这样的模型可以描述基本的神经元对于外界输入电流 (Injected current, 或者建模的突触输入)的相应，也可以引入噪声模型，观察神经元发放的稳定性等等。在本文内我会主要讨论一下神经元的建模，应对不同输入电流的响应，噪声模型，以及对发放稳定性(CV, Coefficient of Variation，变异系数)等特性，以及用Python代码对其实现。

这学期我将会更新一系列计算神经科学相关的内容，主要是整理一些本学期Computational Neuroscience课程上学到的东西分享给大家。也非常欢迎大家一起讨论各种计算相关的问题。

LIF 模型的基本原理

一般情况下，神经元的动作电位主要是靠Na+, K+的选择性 on/off dynamics实现的。经典的HH模型将各种离子的电位，及其门控通道等效为一个电池和其受调控的可变导钠的电阻，又吧膜电位的被动特性等效为一个电容。再将以上并联，从而得到一个对神经元电特性的建模。

Hodgkin and Huxley (1952)

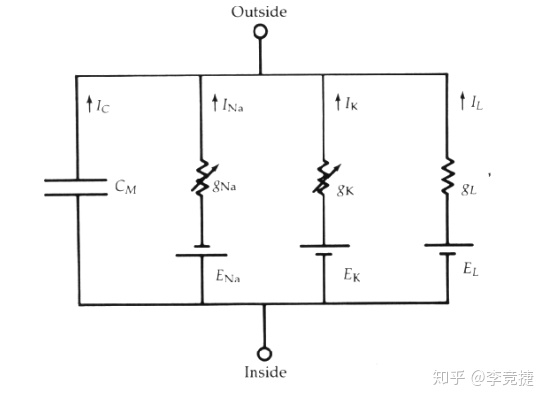
LIF模型忽略了比较brief的动作电位具体的Dynamic，只考虑膜电位的被动特性，以及动作电位的触发，所以LIF模型将HH模型简化为电容+一个电池&可变电阻的并联。同时LIF模型想要建模不同输入电流的影响（用于模拟膜片钳实验的current clamp），因此再并联了一个外部输入的电流源I_app，如下图：

Koch (1999)

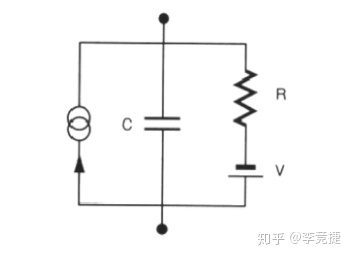
离子通道的电压门控特性靠设定一个threshold来实现，除此之外，LIF模型还考虑了动作电位之后的不应期: 在发放了一个动作电位之后: 神经元会位置在一个reset电位几毫秒。

LIF模型的公式

LIF模型的数学阐述如下: 主要是通过这个公式来描述膜电位的被动特性以及外部输入电流的影响。

这个公式每个部分都代表上图的每个并联的部分，利用基尔霍夫电流结点定律(流入节点的电流=流出节点电流)。在这里

代表细胞膜表面的电容，

，

分别代表Leak的导纳，以及被动平衡的电压 （一般就是静息电位，-70mV）。如果没有外界电流输入，公式还可以改写为时间常数的版本（纯粹的被动特性）。

在存在一个外界的

输入时，膜电位的平衡电位(稳态电位)会升高，一旦膜电位超过一个给定的阈值

后，会产生一个Spike (比如30mV)，并且会将膜电位重置到一个重置电位

并维持一个给定的不应期时间

(以上给定的参数仅为参考)，然后再利用LIF的被动电位公式进行下一步的计算。

通过LIF模型，我们可以计算出一个理论的神经元活动的发放间歇长度(ISI)，从而通过其倒数推算其理论的发放速度 (Firing Rate)。理论的ISI是这样计算的：首先有一个确定的不应期时间

，然后存在一个不应期的电位

，可以通过对微分方程进行求解，得到膜电位从

上升到

所需要的时间，再加上不应期时间

就可以得到每个ISI的时间，再求倒数，得到具体的Firing Rate。可以算出来的 Firing Rate公式推算如下：

其中，

是能触发Spike所需要的最小电流。

LIF模型的简单实现

这里给出我自己写的一个python的函数，利用一阶欧拉法迭代计算该微分方程进行求解，并且对阈值、不应期等情况进行一个计算和区分。

import numpy as np
import matplotlib.pyplot as plt

def calc_next_step(Vm, I, step_t, remaining_refrac_time):
    Vl = -70
    Gl = 0.025
    C = 0.5
    if Vm > -50 and Vm < 0: #threshold
        Vm = 30 #spike potential
    elif Vm > 0:
        Vm = -60 #reset potential
        remaining_refrac_time = remaining_refrac_time*0 + 2 #reset everything to 2
    elif remaining_refrac_time>0:
        Vm = -60 #reset potential
        remaining_refrac_time -= step_t
    else:
        Vm = Vm + step_t*(-Gl*(Vm-Vl) + I)/C
    if remaining_refrac_time<0:
        remaining_refrac_time = remaining_refrac_time*0
    return Vm,remaining_refrac_time

step_t = 0.001
t = np.arange(0,500+step_t,step_t)
Vm_out = np.zeros(np.shape(t)[0])
I = 0.9

ind = 0
Vm_out[0]=-70 #init state
remaining_refrac_time = 0
for tt in t[0:-1]:
    Vm_out[ind+1],remaining_refrac_time = calc_next_step(Vm_out[ind],I,step_t,remaining_refrac_time)
    ind += 1


plt.plot(t,Vm_out)
plt.xlabel("time /ms")
plt.ylabel("Memberance Potential /mV")
plt.show()

上述代码模拟外部电流钳输入电流

的情况，代码会产生如下结果：

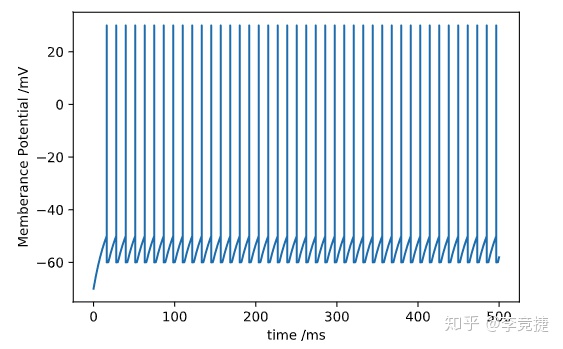
可以看到，该模拟的细胞会产生一个持续恒定的动作电位。

通过给定不同的输入电流

，我们可以得到不同Firing Rate的一个序列，如下图。可以看到再输入电流小于一定程度（在这个例子里是0.5nA）时，由于稳态的膜电位达不到阈值，不会触发spike，但是当其高于阈值后，输入电流越大，Firing Rate也越快。

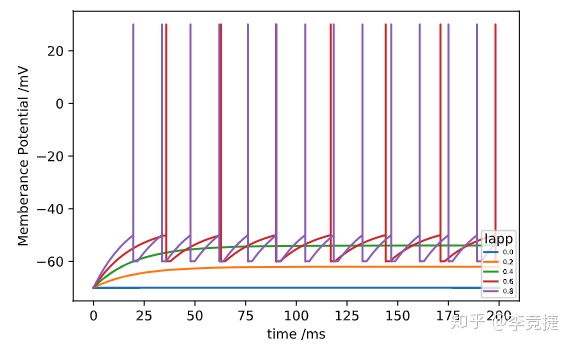
在这里 输入电流0.5nA相当于一个bifurcation point，在这里分叉出来两种截然不同的情况：firing or not firing。

LIF模型的性能分析，Firing Rate，以及噪声

接下来，我试图量化LIF模型，对不同输入电流的情况会产生不同Firing Rate的关系：我通过分别计算1）直接模拟神经元，计算实际Firing Rate，以及2）LIF模型理论可以产生的Firing Rate来进行对照。得到的结果如下图：可以看到两种方式计算出来的Firing Rate，和输入电流的关系基本是一致的

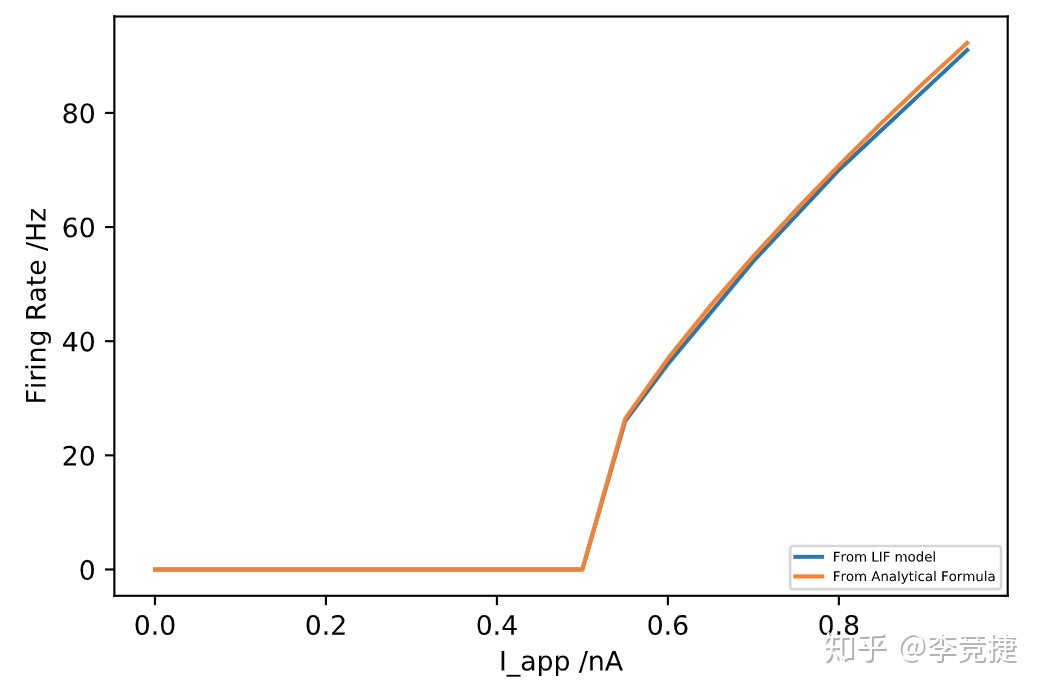
理论的LIF模型仅模拟了理想情况，无噪声时会产生的情形。于是接下来我对LIF模型加入噪声进行模拟，此时LIF模型的微分方程如下：

这种对于噪音的微分方程迭代求解方法如下：需要注意跟号

这里给出一个微分方程求解的函数：

def calc_next_step_noise(Vm, I, step_t, remaining_refrac_time,sigma):
    Vl = -70
    Gl = 0.025
    C = 0.5
    wn = np.random.normal()
    if Vm > -50 and Vm < 0: #threshold
        Vm = 30 #spike potential
    elif Vm > 0:
        Vm = -60 #reset potential
        remaining_refrac_time = remaining_refrac_time*0 + 2 #reset everything to 2
    elif remaining_refrac_time>0:
        Vm = -60 #reset potential
        remaining_refrac_time -= step_t
    else:
        Vm = Vm + step_t*(-Gl*(Vm-Vl) + I)/C + sigma*np.sqrt(step_t)*wn
    if remaining_refrac_time<0:
        remaining_refrac_time = remaining_refrac_time*0
    return Vm,remaining_refrac_time

带着有噪声的模型，再跑一遍各种输入电流的情况，得到的结果如下图：

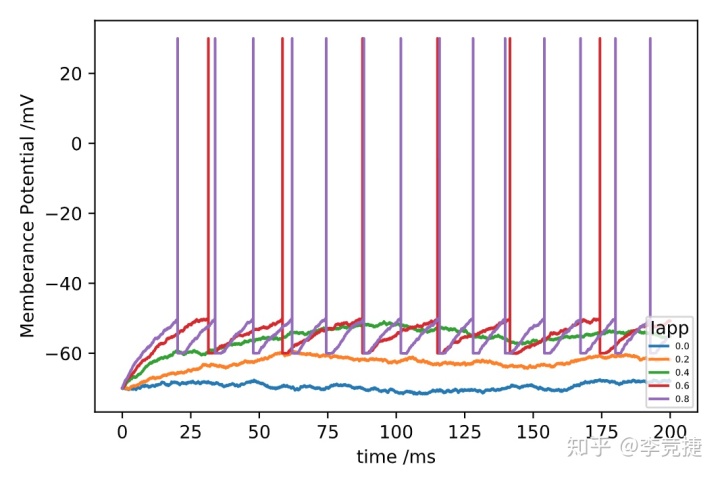
我们可以看到，存在噪声的情况下，即使原先不会达到阈值电位的比较低的输入电流的神经元也可能会达到阈值并触发动作电位。对于输入电流在阈值附近的情况，噪声会产生比较大的影响，也会对ISI产生很大的波动(红色的线)。而对于紫色的，比较大的输入电流的情况，噪声对于ISI影响有限。这里画出引入噪声和不引入噪声，Firing Rate和输入电流关系的对比，如下图：

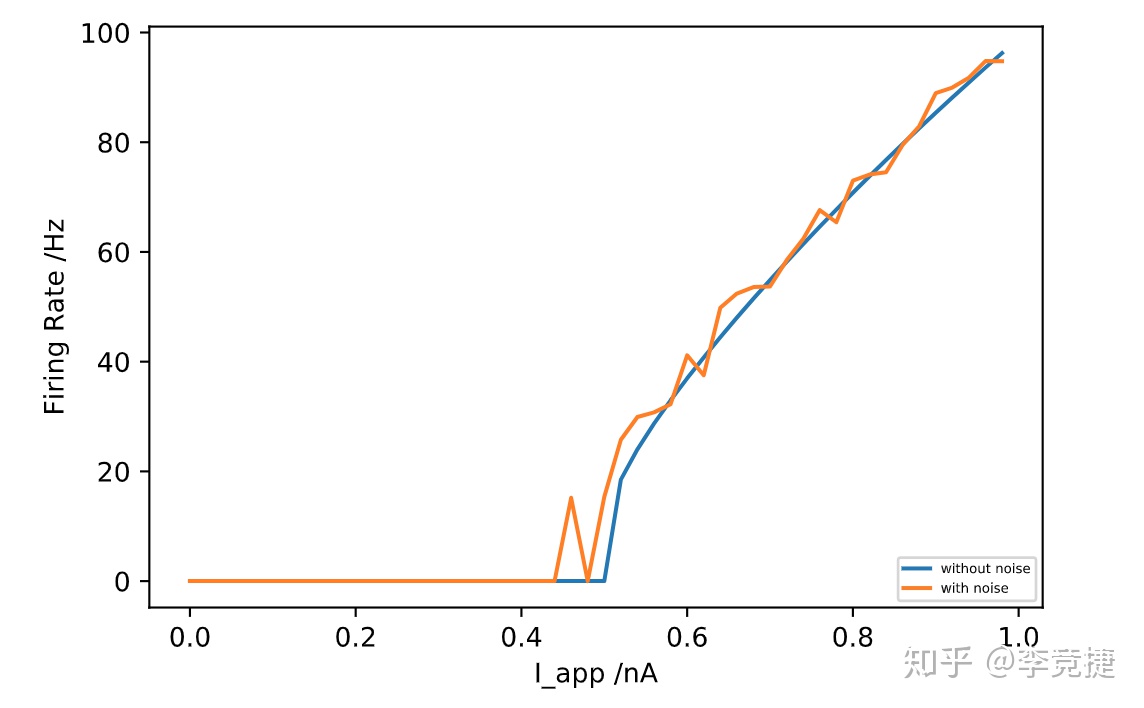
可以看到，再阈值附近，容易产生比较大的波动，不过随着输入电压的提高，噪声带来的相对误差会不明显很多。（其实我应该画一下相对的误差，用Firing Rate做个normalization，毕竟对于80Hz/82Hz，1Hz/3Hz差别还是很大的）

噪音也会让bifurcation point变得不明显。

在这里引入一个统计量：变异系数(coefficient of variation, CV)，来衡量Firing Rate的随机程度。类似的统计量还有Fano Factor，都是衡量随机程度的。

这里提一句题外话：对于一个泊松随机的序列，CV=1，但是其实在大脑，尤其是前额叶的实际测量可以发现CV其实是大于1的，如果以泊松随机来建模的话，我们可以认为泊松随机的参数

也是随时间而变化的，所以可以看到大脑内部加载的信息量所带来的混乱程度是很高的（Goris et al. 2014）。

CV计算方法如下：

我这里还有一个Python函数的例子，通过给定电压序列，先计算ISI（通过求Spike差分），再计算CV：

def extract_CV_from_voltage(voltage,step_t):
    spike_cv = np.zeros(np.shape(voltage)[0]) 
    for ii in np.arange(0,np.shape(voltage)[0],1):
        idx_spike = np.transpose(np.argwhere(voltage[ii,:]==30))
        idx_spike_diff = np.diff(idx_spike)*step_t
        if len(idx_spike_diff[0]):
            mean_isi = np.mean(idx_spike_diff) #mean ISI
            std_isi = np.std(idx_spike_diff)
            spike_cv[ii] = std_isi/mean_isi
        else:
            spike_cv[ii] = 1
    return spike_cv

然后我画出Firing Rate和CV的关系，如下图：每个点代表一次模拟，对于不同的输入电流

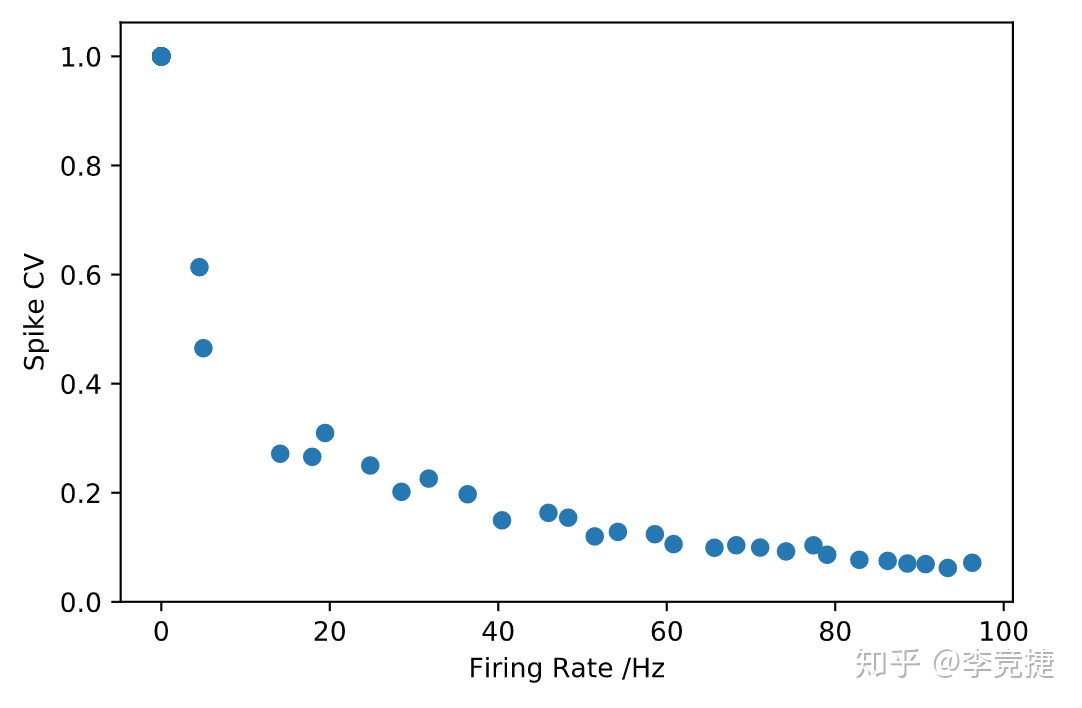
我们可以看到，对于LIF模型，随着Firing Rate的提高，神经元发放的稳定性也会逐渐提高，CV会逐渐下降。对于数学好的朋友，这个CV也是可以推导出来的(Ricciardi 1977; Renart et al. 2003)公式如下：

总而言之，LIF模型是一种建模神经元spike的比较简单基本的模型，忽略了动作电位自身的快速特性：基本只考虑了细胞的被动特性，以及动作电位threshold的特性和refreactory period的特性。但是他可以很好的展示一些神经元动作电位序列的一些特征：比如CV，对噪声的影响之类。

我不会讲HH模型的具体内容，这个很多人说。下一篇文章我开始谈谈对于神经元之间突触传递的建模。有两种方法：Current Based or Conducatance Based. 同时还有三种模型: Kick Model, Filter Model and Kinetic Model. 以及一些对于LTP，LTD的建模。欢迎大家持续关注。

References

主要来自于不知道怎么引用的上课课件和讲义。。。还有

Hodgkin, A. L., & Huxley, A. F. (1952). A quantitative description of membrane current and its application to conduction and excitation in nerve.The Journal of physiology,117(4), 500.

Koch, C., & Schutter, E. D. (1999). Biophysics of computation: Information processing in single neurons.Nature,398(6729), 678-678.

Ricciardi, L. M. (1977). Diffusion Processes and Related Topics in Biology. Springer, Berlin.

Renart, A., Brunel, N., & Wang, X. J. (2003). Mean-field theory of recurrent cortical networks: working memory circuits with irregularly spiking neurons.Computational neuroscience: A comprehensive approach, 432-490.