最优停止理论的推导_37%法则没有完美的选择，只有最优的策略

你可能听过“麦穗理论”：

一个智者带着三个人来到一片麦田前，说：你们进麦田里一直往前不要回头，摘下一支最大的麦穗。

第一个人很快就看见一支又大又漂亮的麦穗，于是就很高兴地摘下了这支麦穗。但继续往前走时发现有很多麦穗比他摘的那支要大得多。

第二个人吸取了第一个人的教训。每当想摘时，就提醒自己，后面还有更大的。结果他走到了终点，却一支麦穗都没摘。

第三个人吸取了前两个人的教训。一开始，他只观察不下手，在心中把麦穗分为”大“、”中“、”小“三类；然后他开始观察验证自己的判断是否正确；在确定自己的判断没有问题后，他摘下了之后遇到的第一支属于”大“类的麦穗。

显然第三个人更聪明，那这个度，如何把握，那就用37%法则：

37%法则是指，在统计学中，对样本数量固定(每个样本只出现一次)的情况下，面对选择其中最优的那个样本这个问题时，如何保证选择的样本尽可能最优的一种策略。就是把样本总量的前37%的样本做为参考，其中的最优的那个作为对照点，如果在剩下63%的样本中，出现比对照点好的样本，就果断选择它。

▍37% 法则应用

买房子问题：一个月内买到合适的房子，把这个月分成两个阶段。第一阶段：只看不买。第二阶段(第12天开始)：一旦遇到一个比第一阶段那个最好的房子好的房子，就毫不犹豫的买下。

找结婚对象问题：一个女孩子，从18岁开始找对象，设定目标是40岁前结婚，根据37%法则，她的两个阶段是26.1岁。26.1岁之前是观察期，她应该只交往不结婚，26.1岁之后是决策期，一旦遇到一个比之前所有遇到的都要好的人，就应该立马把他拿下。

▍延伸阅读

当事情达成某种平衡时，我们在做决定的时候应该如何去思考？如何找打这个平衡点，能让我们的决定更加明智？

当你遇到一个有感觉的人时，有两个陷阱：

一是像没吃过糖的孩子，哭着喊着要海枯石烂真爱到永远；

二是不甘心，心想后面会不会还有更好的呢？

“科学”的做法是：

• 年轻时多恋爱，拒绝把遇到的任何人当作人生伴侣，直到你熟悉恋爱市场的行情。

• 这个阶段一旦过去，选择接下来出现的第一个比之前所遇都要好的人。

这个阶段的数值是多少呢？

“最优停止理论”给出了答案：37%。

你停止找寻并和最佳人选安定下来的概率(用P代表)，与潜在恋人(n)中被你拒绝的人数(r)是相关联的，公式如下：

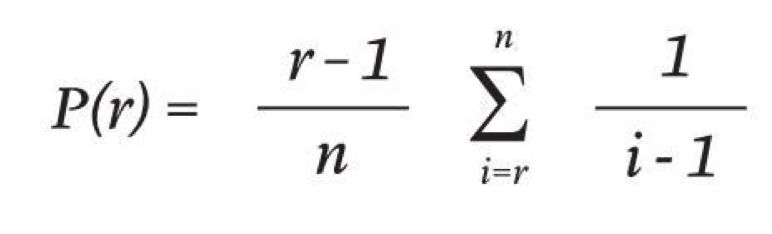
比方说吧，如果你一生可能要有10段恋爱，那么找到“那个他”的最大概率发生在拒绝4个恋人之后(代表39.87%的恋爱经历)。

如果你可能谈20段恋爱，则要拒绝前8个人(那个对的人在38.42%处等你)

什么是最优停止理论，37%这个数字又是如何推导出来的？这就不得不提最优停止理论的一个经典案例：秘书问题。

我们在公司中工作，被招聘、面试人都有所经历，假如你是一个秘书，需要招聘一个人员，筛选了几分简历，决定面试4人，甲、乙、丙、丁。

每次面试之后，你有两个选择，要么聘用此人，要么拒绝。我们如何才能招聘最佳人选的机会最大，终止面试呢？

我们假设这四个人按照顺序丁＞丙＞乙＞甲，我们面试是随机的，前提也不知道丁是最棒的，如果我们面试完这四个人，是有24种可能的，也就是4种排列。

假如我们有三种策略：

第一种策略：面试完第一人就决定录用，能录用到丁的概率是25%；

第二种策略：面试完最后一人就决定录用(前三人不要)，能录用到丁的概率是25%；

第三种策略：面试完第一人不做决定，作为判定标准，一旦出现比他高的人就录用，能录用到丁的概率是46%。假如第一个人是就是丁，后面面试的能力都比他弱，我们就自行放弃吧，选中丁的概率是为0的；假如第一个人是甲，第二个人能力都比甲好，但是录取到丁的概率是2/24；假如第一个人是乙，第二个人是甲的话，肯定不用，第二个人是乙、丙、丁就会录用，但是能录用到丁的概率就是3/24；假如第一个人是丙，只有丁比他强，因此只要丁一出现就会被录取，有6/24的可能性，以上可能性加到一起就是11/24=46%。我们发现第三种策略能选到最优人员的概率要大。

注：以上计算各位可自行搜索，或是自己列一下24个排序，就可以计算出来。

以上是N=4的时候，当N变动时，概率是什么样子的呢？

请看下表：

当N无限大，我们作为标准的策略就是N/e(e是自然常数)，概率就是1/e，是不是很神奇。假如人数是10000,，我们采取的策略是10000/2.71828=3678，不做录取，只做标准，选中最优人员的概率为1/e=36.8%≈37%。

这就是37%的由来，因此37%是我们在做最优停止时选择标准根据样本计算的依据。