多元函数概念思维导图_思维导图全解二次根式、平面直角坐标系及函数的性质概念...

二次根式、平面直角坐标系及函数，在初中数学中，占有一定的考试比例。通过思维导图总结的内容，不过是一两张纸而已，但是真正要学会弄懂，需要不断地进行运算、练习。

学习二次根式要明确二次根式的定义，以及有意义的条件，区分同类二次根式，并且能够运用二次根式进行加减乘除运算。

学习平面直角坐标系，要区分坐标轴上的坐标点，以及各象限，角平分线所处的位置，学会向上、向下、向左、向右平移坐标轴上的点。通过运算求出，点到坐标轴的距离。概念要清晰，公式要铭记。

学习函数及其图像，要知道函数的基本表达式，自变量的取值范围，几何图形中动点的问题，用函数图像来解决实际问题。思维导图基本内容如下：

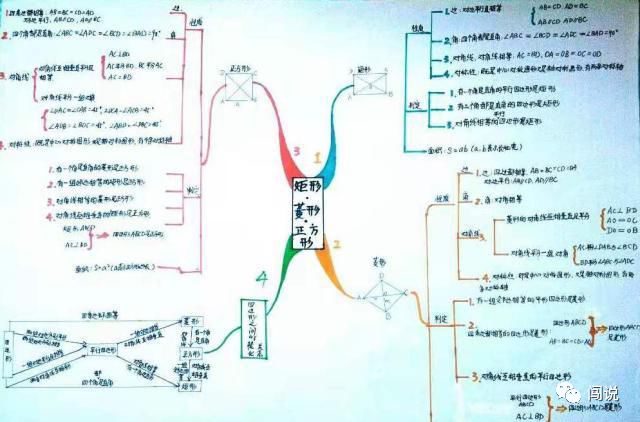
1、矩形，性质、判断、面积公式

2、菱形，性质、判断、面积公式

3、正方形，性质、判断、面积公式

4、四边形之间的转换关系。

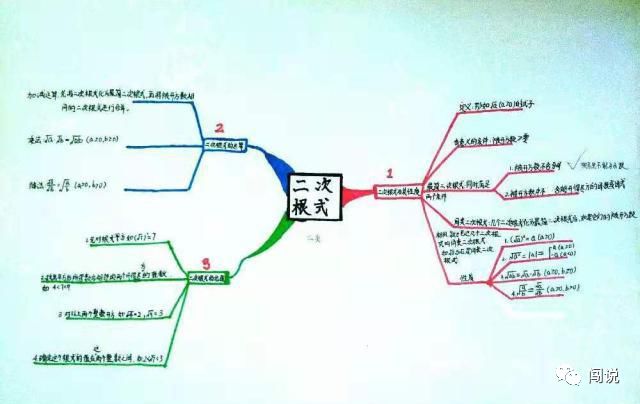
二次根式会经常作为考试的重点，需要掌握二次根式的概念，性质以及运算。

二次根式的性质，在思维导图中分为4种，请务必记住学会。

二次根式的运算，包括加法运算，乘法运算，除法运算。

二次根式的估值，方法为，1、先对根式平方，2, 找出平方后所得数字相邻的两个开得尽方的整数。3、对以上两个整数开方。4、确定这个根式的值在这两个整数之间。

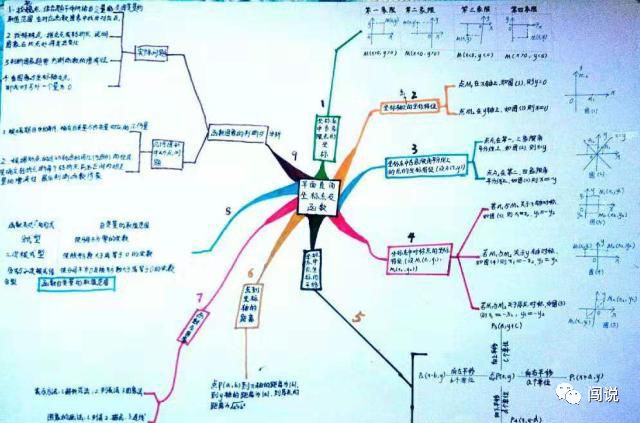
平面直角坐标系，1、用图示法确定坐标系中各个项的坐标，2、观察坐标轴上点的坐标特征，3、坐标系中各象限角平分线上点的坐标特征，4、坐标系中对称点的坐标特征。5、学会坐标系中点坐标的平移，6、点到坐标轴的距离。

函数，1、函数及其图像的表示方法，2、函数表达式的形式及函数自变量的取值范围，3、函数图像的判断与分析。

结束语：好了，今天小编的文章就到此结束了，感谢各位朋友的阅读。每一篇文章，都是小编用心写的，收集了许多的资料，实属不易！如果各位阅读的朋友觉得小编今天写的文章不错，那么就麻烦各位朋友高抬金手，在文章末尾为小编点一个小小的赞，各位朋友的赞，将会让小编高兴一整天，也会成为小编继续努力的动力！同时如果各位朋友喜欢小编写的文章，可以给小编点点关注，好让小编拥有这份荣幸，继续为各位朋友创作优质的文章！