两组声音的一维数据如何比较相似度_多维数据的Q-Q Plot检验

零、写在最前

想分享这个内容的原因是题主最近在跟Prof.Chirikjian做毕设，而在处理数据的时候用到了Q-Q Plot这个检验。当我自己在找资料的时候，大部分找到的都是一维数据的处理方法，因为我在求解机器人的estimation，所以是多维数据。因此呢，就将如何对多维数据进行Q-Q Plot检验分享一下。

一、什么是Q-Q Plot

这个Q-Q Plot首先肯定跟那个企鹅没什么关系，这里指的是Quantile，中文翻译过来就是分位数，即横纵坐标轴均为分位数，通常x轴为理论分位数（theoretical quantile），y轴为样本分位数（sample quantile）。两个分位数的比值越接近于1，则表明样本与分布的关联度越高，可以给定阈值判断是否接受假设，反映到Q-Q Plot上就是这些点是否在

这条直线附近，若在阈值接受范围内，则可接受这些数据来自假设分布的假设，反之拒绝。关于什么是分位数，可以简单理解一下，想象你是一个班级的班主任，在一次考试后你想要看一下前50%的学生考了多少分，你就会先将所有分数从小到大排列一下，然后找到排名50%的分数，而这个分数假设为60分，则分位数

。我们先从一维数据入手看看怎么寻找这两个分位数。

二、一维数据的Q-Q Plot

先来看看样本分位数（sample quantile），对于一维数据来说就很简单了，直接将数据有序排列作为分位数，即

，这样我们就找到了y轴的值。接下来看看理论分位数（theoretical quantile），首先先来看一个概念，这个概念叫做累积分布函数（cumulative distribution function），即CDF，定义为，

给定一个概率密度函数PDF，

，CDF满足

，可以理解为给定一个

，小于该值的概率。由于CDF为单调递增函数，所以一定存在逆函数，记为

，给定定义对于一维数据，理论分位数

，

。解释一下，这里括号里面的式子，采用的是二分位数的取点方法，当然可以有其他方式，只不过这种方式比较方便，举个例子来解释一下，假设现在某个随机样本有5个数据，记作

，现在我们假设他们来自正态分布，那么第一步就是找到这组数据的期望

和方差

作为模型参数，从而可以找到对应的CDF，根据二分位数公式找到理论分位数，这里先说明一下，为什么要选择二分位数，看一下下面这幅图，

理论分位数选择

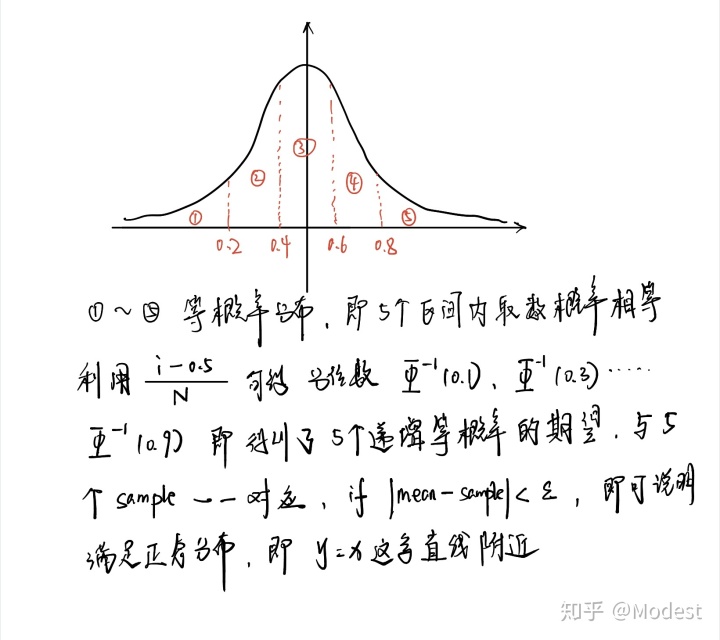
接下来看看结果，

Q-Q Plot

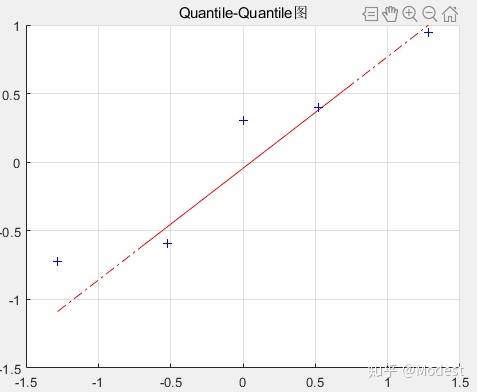
可以看出在样本数量比较少的情况下，效果并不明显，当然随着样本数量增大，根据大数定律，视觉效果会更加明显。反正，明显偏离

这条直线我们就可以说可以拒绝假设的分布成立。至此，我们已经熟悉了如何利用Q-Q Plot对一维数据进行分布假设检验。接下来看看多维。

三、多维数据的Q-Q Plot

经过了前面的介绍，我们知道了做出Q-Q Plot的四个步骤，首先寻找样本数据关于假设分布模型的参数，（例如假设分布为高斯分布，寻找期望

和方差

），然后寻找样本分位数，并将其从小到大有序排列，接下来寻找假设分布的理论分位数，最后作图，观察与给定阈值比较判断。

我们易知，对于一维数据，我们直接利用样本值当作样本分位数即可，但是如果这个数据是个向量怎么办呢，向量无法排序。这时候我们可以利用马氏距离（Mahalanobis distance），它表示一个样本与一个分布的距离，即相似度，我们可以想一下，马氏距离可以想做是将不同维度标准化进行比较，定义为，

,这样我们就可以根据相似度对n维向量进行有序排列了，这里我们选择马氏平方距离作为样本分位数，至于原因，最常用的分布就是高斯分布，而多维高斯分布就是马氏平方距离

的函数，想想后面要用到CDF跟PDF的关系你就可以理解了。

如果对马氏距离感兴趣，可以参考下面这篇文章。

Ph0en1x：马氏距离(Mahalanobis Distance)​zhuanlan.zhihu.com

选择完样本分位数后，下一步就是寻找理论分位数，同样的我们要先找到对应假设分布的CDF，这里举一个例子，假设分布为高斯分布，那么多维高斯分布的CDF可以利用上述积分公式找到，最后求得正好是卡方分布（chi-square distribution），对应的自由度即样本维度，下面这段代码是按照维纳过程随机运动的二维机器人poses，一共10000个样本，验证一下它是否满足笛卡尔坐标系下的高斯分布。

T=1;N=1000;dt=T/N;D=2;L=10000;
x0=0;y0=0;theta0=0;xend=1;yend=0;
v=1;l=0.200;r=0.033;

w1 = v/r;
w2 = v/r;


for i=1:L
   randn('state',i+1)
   dW1 = sqrt(dt) * randn(1,N);
   randn('state',i+10002)
   dW2 = sqrt(dt) * randn(1,N); %Wiener process
   xtemp=x0;
   ytemp=y0;
   thetatemp=theta0; %Initialization
   for j=1:N
      xtemp = xtemp+((r*cos(thetatemp)*(w1+w2)*dt)/2)+((sqrt(D)*r*cos(thetatemp)*(dW1(j)+dW2(j)))/2);
      ytemp = ytemp+((r*sin(thetatemp)*(w1+w2)*dt)/2)+((sqrt(D)*r*sin(thetatemp)*(dW1(j)+dW2(j)))/2);
      thetatemp = thetatemp+((r*(w1-w2)*dt)/l)+((sqrt(D)*r*(dW1(j)-dW2(j)))/l);    %kinematic equation with SDE
      x(i,j)=xtemp;
      y(i,j)=ytemp;
      t(i,j)=thetatemp; %store data 
  end
  xf(i)=x(i,N);
  yf(i)=y(i,N);
  tf(i)=t(i,N);%assemble of final pose of each path
end

xm=sum(xf)/L;ym=sum(yf)/L;tm=sum(tf)/L;
mean1 = [xm;ym;tm];

multi=[0 0 0;0 0 0;0 0 0];
for o=1:L
    multi=multi+([xf(o)-xm;yf(o)-ym;tf(o)-tm]*[xf(o)-xm yf(o)-ym tf(o)-tm]);
end
cov1 = multi/L;

d1=zeros(1,L);
for q=1:L
    d1(q)=[xf(q)-xm yf(q)-ym tf(q)-tm]*inv(cov1)*[xf(q)-xm;yf(q)-ym;tf(q)-tm];
end
d2=sort(d1);

x=0:100;
y=x;
pt=((1:L)-0.5)/L;  
x2=chi2inv(pt,3); 
scatter(x2,d2','*'),hold on
plot(x,y);

看一下结果，

笛卡尔坐标系下运行结果

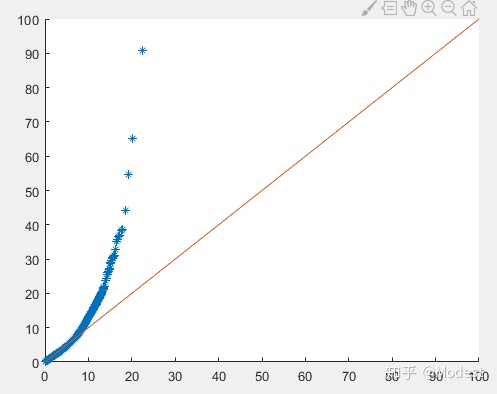
结果很明显，并不满足笛卡尔坐标系下的高斯分布，换一个思路，进行坐标变换，变换到指数坐标系中，即李群空间中，看一下结果，

指数坐标系下运行结果

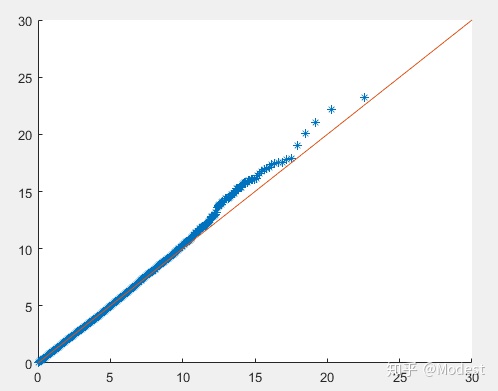
这次结果会好一点，后续进行阈值检验，在给定阈值条件下，不能拒绝该假设，这样就完成对多维数据的Q-Q Plot test。

四、结语

这种检验方法常常被用在高斯分布，卡方分布，学生t分布等模型验证上，与常用的参数检验或非参数检验相比，比较直观，除此之外，也可以用于检验两个样本是否来自同一分布，当然这时的直线斜率不一定就是1了。希望对你有用。