程序中判断一个三角形是不是等腰直角三角形的代码_初中数学 | 三角形知识点总结...

点击上方“蓝字”关注我们吧！ 三角形知识点总结

三角形的有关概念

1.三角形：由不在同一直线上的三条线段首尾顺次相接组成的图形叫三角形。

 三角形的特征：①不在同一直线上；②三条线段；③首尾顺次相接；④三角形具有稳定性。

2.三角形中三条重要线段：角平分线、中线、高

(1)角平分线：三角形的一个内角的平分线与这个角的对边相交，这个角的顶点和交点之间的线段叫做三角形的角平分线。

(2)中线：在三角形中，连接一个顶点和它的对边中点的线段叫做三角形的中线。

(3)高：从三角形的一个顶点向它的对边所在直线作垂线，顶点和垂足间的线段叫做三角形的高。

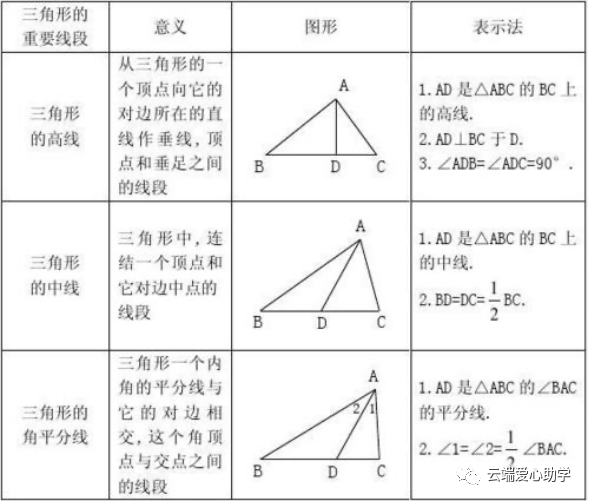
说明：①三角形的角平分线、中线、高都是线段。②三角形的角平分线、中线都在三角形内部且交于一点；三角形的高可能在三角形的内部(锐角三角形)、外部(钝角三角形)，也可能在边上(直角三角形)，它们(或延长线)相交于一点。

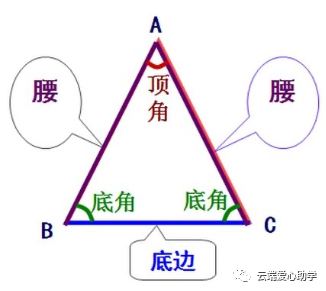
等腰三角形的性质和判定

1.性质

(1)等腰三角形的两个底角相等(简写成“等边对等角”)；

(2)等腰三角形的顶角的平分线，底边上的中线，底边上的高重合(简写成“等边三角形三线合一”)；

(3)等腰三角形的两底角的平分线相等(两条腰上的中线相等，两条腰上的高相等)；

(4)等腰三角形底边上的垂直平分线到两条腰的距离相等。

(5)等腰三角形的一腰上的高与底边的夹角等于顶角的一半。

(6)等腰三角形底边上任意一点到两腰距离之和等于一腰上的高(等面积法可证明)；

(7)等腰三角形是轴对称图形，只要有一条对称轴，顶角平分线所在的直线是它的对称轴，等边三角形有三条对称轴。

2.判定

在同一三角形中，有两条边相等的三角形是等腰三角形(定义)。

在同一三角形中，有两个角相等的三角形是等腰三角形。(简称：对角对等边)

三、直角三角形和勾股定理

    1.直角三角形的定义：有一个角是直角的三角形是直角三角形，在直角三角形中，斜边中线等于斜边的一半；30度所对的直角边等于斜边的一半；直角三角形常用面积法求斜边上的高。

    2.勾股定理：直角三角形两直角边a，b的平方和等于斜边c的平方，即a₂＋b₂＝c₂。

勾股数一定是正整数，常见勾股数：3,4,5；5,12,13；6,8,10,；7,24,25；8,15,17；9,12,15。

方法总结

    当不明确直角三角形的斜边长，应把已知最长边分为直角边和斜边两种情况讨论。无理数在数轴上的表示和线段长表示通常用到勾股定理。翻折题型常用勾股定理(口诀：翻折求边找直角，勾股定理设未知量)

    如果三角形的三边长a，b，c有关系a₂＋b₂＝c₂，那么这个三角形是直角三角形。勾股定理的逆定理，常用于判断三角形的形状，先确定最大边(可以设为c)。

三角形中的中线定理

1.定理内容：三角形一条中线两侧所对边平方和等于底边的    一半平方与该边中线平方和的2倍。

2.中线的定义：任何三角形都有三条中线，而且这三条中线    都在三角形的内部，并交于一点。由定义可知，三角形的    中线是一条线段。

3.由于三角形有三条边，所以一个三角形有三条中线。

4.重心：且三条中线交于一点。这点称为三角形的重心。

5.每条三角形中线分得的两个三角形面积相等。

直角三角形的判定

判定1：有一个角为90°的三角形是直角三角形。

判定2：若a的平方+b的平方=c的平方，则以a、b、c为边的三角形是以c为斜边的直角三角形(勾股定理的逆定理)。

判定3：若一个三角形30°内角所对的边是某一边的一半，那么这个三角形是以这条长边为斜边的直角三角形。

判定4：两个锐角互余的三角形是直角三角形。

判定5：证明直角三角形全等时可以利用HL，两个三角形的斜边长对应相等，以及一个直角边对应相等，则两直角三角形全等。[定理：斜边和一条直角对应相等的两个直角三角形全等。简称为HL]

判定6：若两直线相交且它们的斜率之积互为负倒数，则这两直线垂直。

判定7：在一个三角形中若它一边上的中线等于这条中线所在边的一半，那么这个三角形为直角三角形。

勾股定理的逆定理

    如果三角形三边长a，b，c满足，那么这个三角形是直角三角形，其中c为斜边。

①勾股定理的逆定理是判定一个三角形是否是直角三角形的一种重要方法，它通过“数转化为形”来确定三角形的可能形状，在运用这一定理时，可用两小边的平方和与较长边的平方作比较，若它们相等时，以a，b，c为三边的三角形是直角三角形；若时，以a，b，c为三边的三角形是钝角三角形；若时，以a，b，c为三边的三角形是锐角三角形；

②定理中a，b，c及只是一种表现形式，不可认为是唯一的，如若三角形三边长a，b，c满足，那么以a，b，c为三边的三角形是直角三角形，但是b为斜边.

③勾股定理的逆定理在用问题描述时，不能说成：当斜边的平方等于两条直角边的平方和时，这个三角形是直角三角形。

※

三角形定理公式

1.三角形的三边关系定理及推论：三角形的两边之和大于第三边，两边之差小于第三边。

2.三角形的内角和定理：三角形的三个内角的和等于180度。

3.三角形的外角和定理：三角形的一个外角等于和它不相邻的两个的和。

4.三角形的外角和定理推理：三角形的一个外角大于任何一个和它不相邻的内角。

5.三角形的三条角平分线交于一点(内心)。

6.三角形的三边的垂直平分线交于一点(外心)。

7.三角形中位线定理：三角形两边中点的连线平行于第三边，并且等于第三边的一半。

撰稿:赵梓伶

审核:鲁军霞

审定:郭思琪

责任编辑:熊倩/焦雅欣/魏秋菊

公众号编辑:杨瀚淩

微信搜一搜 云端爱心助学