几何画板200个经典课件_立体画板2.15教程（4）——课件示例1

教程太长，系统限制不能一次发完成，要分成多段发表.

用户可在以下位置下载全部软件、教程和课件：

www.jianpinghuaban.com

立体画板教程 >课件示例1

立体画板教程 > 课件示例1 >正方体与球

该课件的示例文件为：8球与正方体.chb，作法如下：

1 做坐标平面 ,

2 选择其中一个坐标平面上的对角线上的两个点，执行“构造”“线段”菜单命令，作一条线段。

3 选择该线段，执行“构造”“线段的中点”命令，如下图所示,,这个中点记为点O。

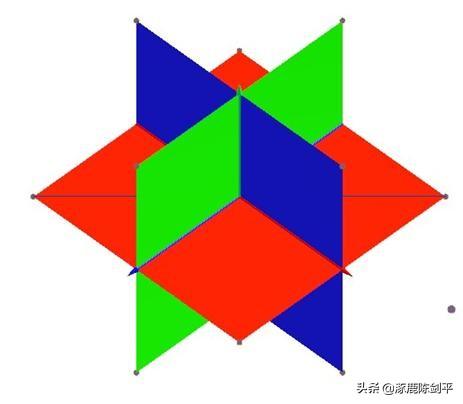
4 点击工具条上的画线段按钮，然后在画板空白处拖动，则画出一条线段，

5 点击工具条上的选择按钮，然后选择这条线段，执行“构造”“线段上的点”命令，则得到线段上的点，如上图所示。依次选择这三个点，执行“显示”“标签。。。”命令，得到下图所示的对话框，点击确定，则得到三个点的标签，如下图

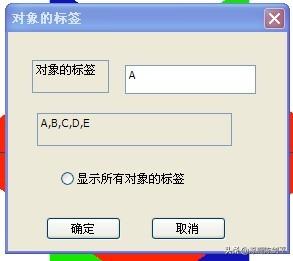
6 依次选择点A，C，选择“变换”“标记向量”命令，

7 选择点O，执行“变换”“平移””命令，得到一个平移点，再选择点O和这个平移点，执行“构造”“球体”命令，得到球体，如图所示

在选择一个点时，若该点被一个平面所挡，可先给这个平面做一个显示按钮，隐藏该平面后再选择这个点，

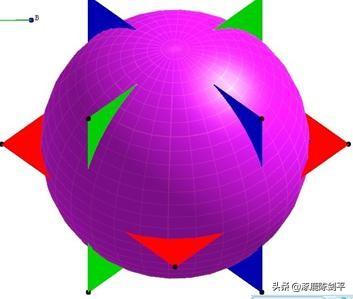
8 移动点C的位置，则球的大小可发生改变

9 选择点C，点击工具条上的“动画”按钮，则得到点C 的动画按钮。点击该按钮，点C的位置开始移动，球的大小自动改变。选择该动画对象，执行“编辑”，“属性”菜单命令，把动画的方向设置为“双向”。

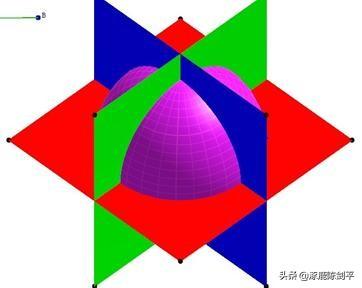
10 还可为坐标平面做一个显示按钮，隐藏某个坐标平面，如下图。

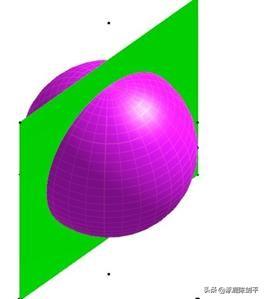
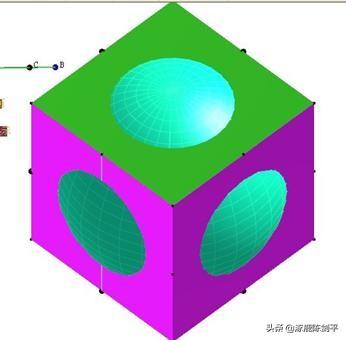
11 做正方体。执行“绘图”，“绘制标准正方体”菜单命令，则得到一个标准位置和大小的正方体如下图所示，从图中可清楚得看到正方体与球体的关系。若球体变小，可隐藏该正方体。

• 立体画板教程 > 课件示例1 >二面角

1 做一个圆，并做圆上的一个点，如下图，选择如图中的三个点对象 执行“构造”“三角形面”命令得到如图所示的三角形面对象，

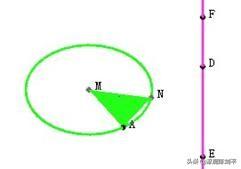
再做一个点D，选择点D和前面所做的面对象，执行“构造”“面的垂线”，选择面的垂线，执行“构造”“线上的点”命令，得到线上的点E,再同样做点F。如上图。

2 再做一个圆上的点P，选择这个点，点击工具按钮“动画”，得到圆上点的动画按钮。

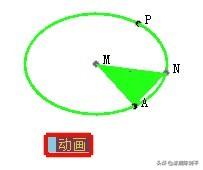
3 依次选择点M,E执行“变换”“标记向量命令”，选择点A,P执行“变换”“平移”命令，得到两个平移点。

依次选择点M,F执行“变换”“标记向量命令”，选择点A,P执行“变换”“平移”命令，再得到两个平移点。选择这4个点，执行“显示”“标签…”命令，在得到的对象框中输入A1，则得到4 个点的标签，如上图。

4 依次选择点A1,A3,F,执行“构造”“四边形面”命令。依次选择点A2,A4,F,执行“构造”“四边形面”命令。得到如图所示的二面角。

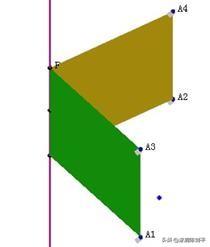
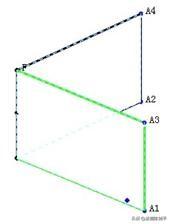
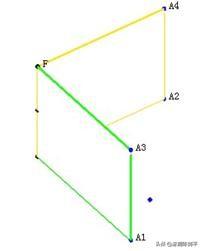
5 点动画按钮，这个二面角可旋转变化。

6 改变点M，A，P，D，E，F的位置，则二面角可发生变形。

7 选择二面角的面，执行“设置”“几何体的类型”命令，也可直接点击有关的按钮，几何体类型也可发生变化，如上图。

8 也可在键盘上按键：J,M,K,I,N,B,以及方向健进行平移，旋转，缩放。

• 立体画板教程 > 课件示例1 >长方体的展开

1 执行“画图2”，“绘制坐标系”菜单命令，执行“设置”，“显示与隐藏坐标系”命令，则得到用户可进行操作的坐标系，并隐藏参考坐标系，如下图所示。

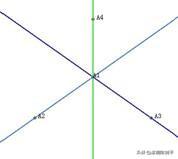
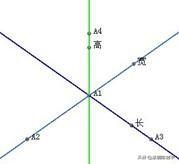
2 点击左上角的做点工具按钮，然后在三个坐标轴上点击，则得到三个坐标轴上的点。也可先选择坐标轴，然后执行“构造”，“线上的点”，也可做出这三个点。分别选择这三个点，执行“显示”，“标签…….”菜单命令，把这三个点的标签分别设置为“长”，“宽”，“高”，如上图。

16.3.3 做一个自由点，标签设置为“顶点”，选择点A1和“顶点”执行“变换”，“标记向量”菜单命令，再选择点“长”，“宽”，“高”，执行“变换”，“平移”命令菜单，则得到平移对象，分别选择这三个点，执行“显示”，“标签……”菜单命令，在标签栏键入“顶点1”，则三个点的标签分别被设置为“顶点2”， “顶点3”， “顶点4”，如下图。

再设置“顶点”到“顶点3”的向量，对“顶点2”进行平移，得的点标签设置为“顶点5”。

再设置“顶点”到“顶点4”的向量，对“顶点2”，“顶点5”，“顶点3”进行平移，得的点标签设置为“顶点6”，“顶点7”，“顶点8”。这时得到了长方体的八个顶点。如下图。

4 执行“数据”，“新建参数”菜单命令，新建一个参数t，数值设置为60.

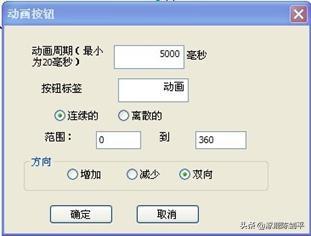
选择这个参数，点击工具按钮“动画”，得到一个对话框，如下图，把范围设置为0到90，方向设置为双向。标签设置为“展开与合并”。选择参数t，执行“变换”，“标记角”菜单命令，把这个参数设置为旋转变换的角。

5 选择顶点4和顶点6(注意次序)，执行“构造”，“线段”菜单命令，得到线段，选择该线段，执行“变换”，“标记轴”菜单命令，选择顶点7和顶点8，执行“变换”，“旋转”命令，得到两个旋转点，标签设置为P,Q.

上面的标记角也可用下面的方法。选择顶点4和顶点6，执行“变换”，“标记轴”菜单命令。

6 再选择“顶点”和“顶点2”，执行“构造”，“线段”命令，选择该线段，执行“变换”，“标记轴”菜单命令，选择点P,Q和顶点4，顶点6，执行“变换”，“旋转”菜单命令，得到4个旋转点。标签分别设置为P1,P2,P3,P4.

在上面的过程中不能选择到顶点4和顶点6，可先给顶点4到顶点6线段设置一个显示按钮，隐藏为条线段。

选择顶点和顶点2，P2，执行“构造”，“平行四边形面”命令，得到一个面对象。同样方法做平行四边形面P1P2P3P4。

7 再分别以顶点2和5的线段为轴，顶点5和3的线段为轴，顶点3和顶点的线段为轴，做出另三个面的展开图。

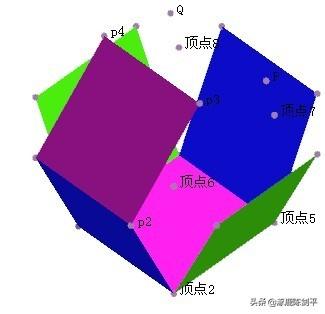
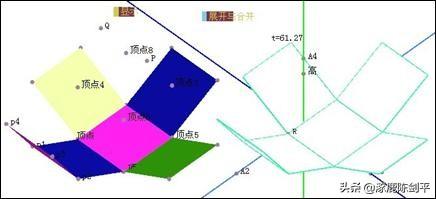
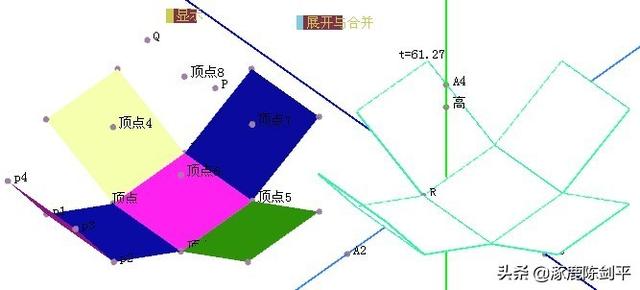
然后可隐藏无关的点，把一些点的大小设置为比较小。

8 做一个自由点，标签设置为R，标记顶点到点R4 向量，选择长方体的六的面，执行“变换”，“平移”菜单命令，选择六个平移的面，点击体类型按钮，把其体类型设置为“线框2”。这样就得到两个展开图，一个是实心体的，一个是线框体的。如下图。

这时移动点“长”，“高”，“宽”，“顶点”，R等，可改变立方体的大小和位置。

9 展开角的大小还可这样设置，选择点A1,A2，构造线段，在线段上做一个点，再依次选择点A1,线段上点，A2，执行“度量”，“比”命令，得到一个度量参数，标签设置为t2，执行“数据”，“计算”菜单命令，做计算t2*90，把计算得到的参数标记为旋转角。这样移动线段上的点，就可对长方体进行展开与合并。

• 立体画板教程 > 课件示例1 >通风塔

做法待续，课件效果如下图所示。(课件在文件：通风塔.chb)

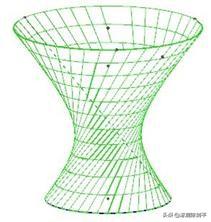
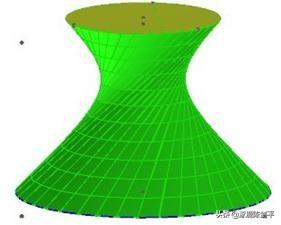
改变上下底半径和高度，可变形为花篮或者纸篓。(见文件：花篮.chb)如上图。

再变形，或变为飓风。(文件：飓风.chb)

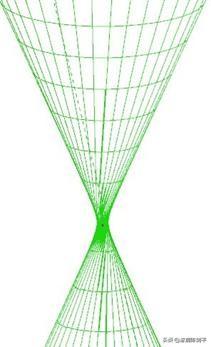
• 立体画板教程 > 课件示例1 >几个组合体

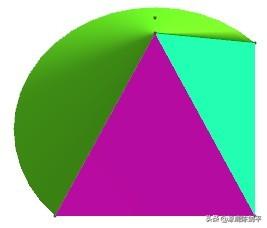
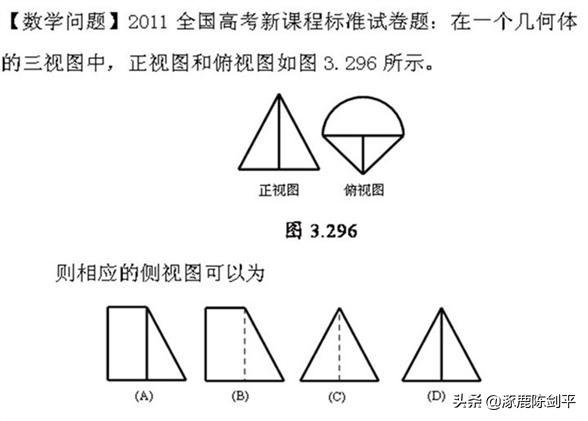
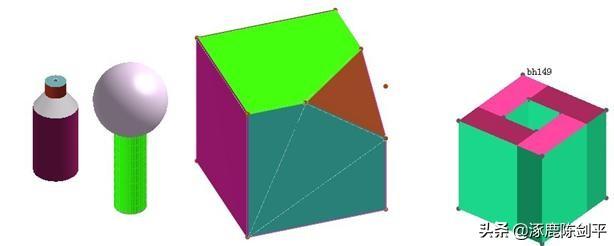
1 课本21页问题(有关三视图)

人民教育出版社新课程标准数学教材必修2第21页的问题：如下图已知几何体的三视图，想象对应的几何体的结构特征，并画出它的直观图。

(所在文件：组合体1.chb)

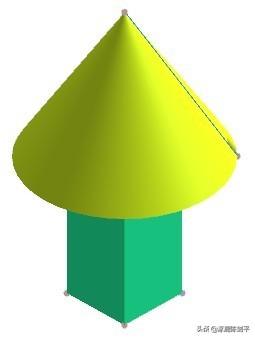
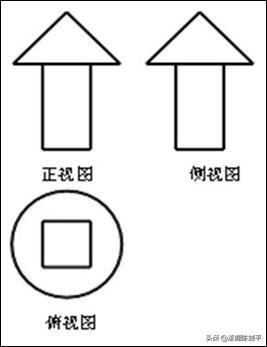
2人民教育出版社新课程标 准数学教材必修2第19页的问题：如下图是一个奖杯的三视图，你能想象出它的几何结构特征，并画出它的直观图吗？

(见文件：组合体2.chb)

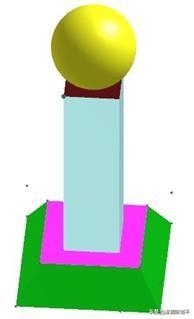
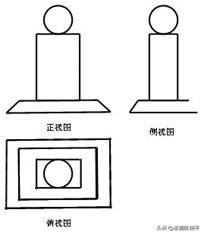
3(所在文件为：组合体3.chb)

• 立体画板教程 > 课件示例1 >一道高考题

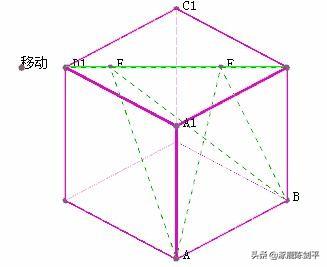
09宁夏题：2009年高考宁夏海南试卷题：如图，正方体ABCD-A1B1C1D1的棱长为1，线段B1D1上有两个动点E,F，且EF=

,则下列结论中错误的是

(A)

(B) EF平行于 平面ABCD (C) 三棱锥A-BEF的体积为定值 (D) 异面直线AE,BF所成的角为定值。(所在文件：高考题1.chb)

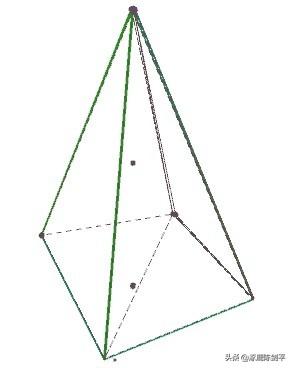
• 立体画板教程 > 课件示例1 >棱锥棱台棱柱的结构特征

作法待续：

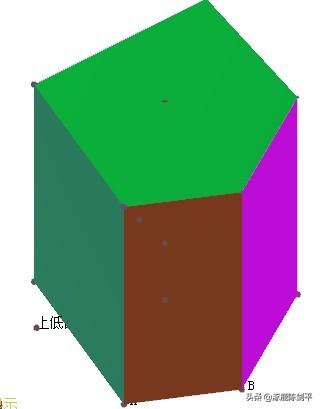
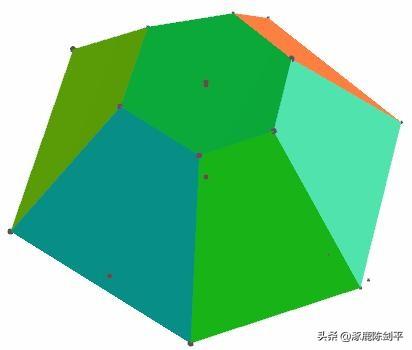
• 立体画板教程 > 课件示例1 >杠铃

做法待续：(插图所在文件：杠铃.chb)

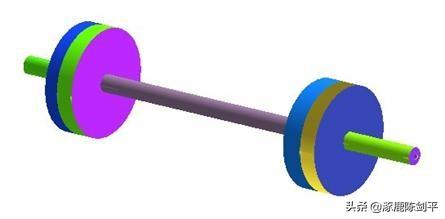
• 立体画板教程 > 课件示例1 >正方体的三视图

做法待续：(插图所在文件：1立方体的三视图.chb)

点击按钮“长方体的控制点”，可显示出长方体的6个控制点，移动这6点的位置可以改变长方体的形状。点击按钮“投影1”等，可演示投影过程。

用同样的方法你可做出任意几何体的三视图。

还可以旋转三个投影图，把他们旋转到同一个平面上，这更易于学生的理解。

• 立体画板教程 > 课件示例1 >认识常见的几何体

做法待续：(插图所在文件：2认识常见的几何体2页.chb)这是课本上第2页的课件

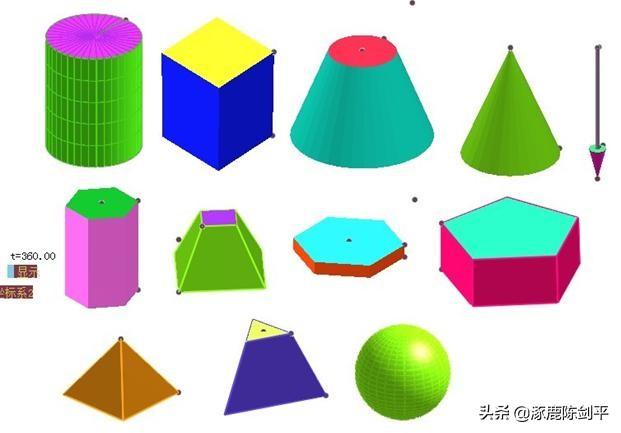
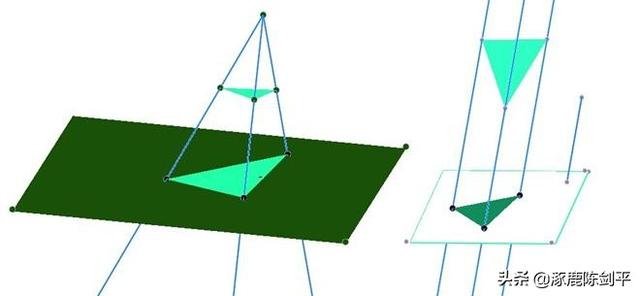
• 立体画板教程 > 课件示例1 >中心投影与平行投影

做法待续：(插图所在文件：9中心投影.chb)

• 立体画板教程 > 课件示例1 >简单组合体的结构特征

做法待续：(插图所在文件：10简单组合体的结构特征(6页).chb)这是课本上第6页的课件

• 立体画板教程 > 课件示例1 >人教版课本问题

必修2课本问题

画出下图中L围绕l旋转一周形成的空间几何体(插图所在文件：13课本35页2题.chb)

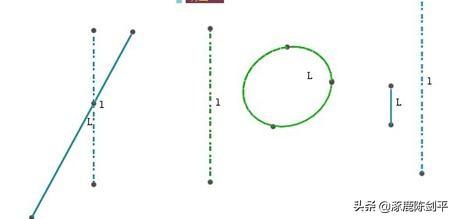
执行“绘图”、“绘制坐标系”命令，绘制坐标系。在OX轴上做点A,B。再在空间任意做一个自由点C，选择点O,C，执行“变换”，“标记向量”命令，再选择点A,Z,B，执行“变换”，“平移”菜单命令，则得到三个平移点，如下图。

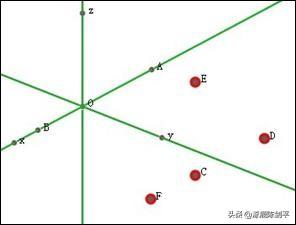
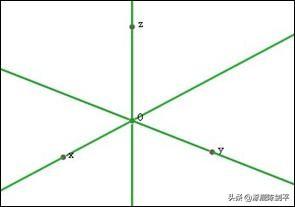
依次选择点C,D,E,执行“构造”，“圆”菜单命令，得到一个圆。选择点F和Z轴，执行“构造”，“平行线”命令，得到一条平行线。移动点A和B，则可改变这个圆的大小和平行线的位置。

选择这个圆，执行“构造”，“圆上点”命令，则到一个圆上的自由点，标签设置为G，再依次选择点D,E,G,执行“构造”，“三点弧”命令，得到一个三点弧对象。移动点G的位置，与点D重合。则三点弧变成一个圆。

之所以要这样做是因为画板目前没有做圆的旋转体功能。

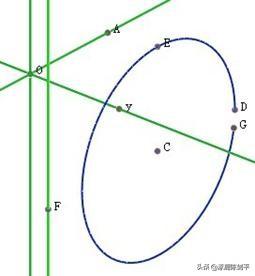
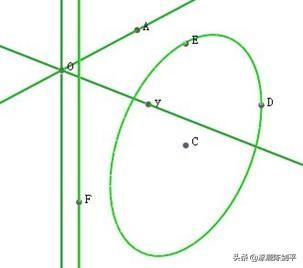
再新建一个参数，并为参数做一个动画按钮。依次选择选择圆弧，平行线，参数，执行“构造”，“旋转体”，则得到如图所示的旋转体。改变几何体的属性为不封闭，增加纬密度，得到下图，点击动画按钮，则可得到不同旋转度数的旋转体。

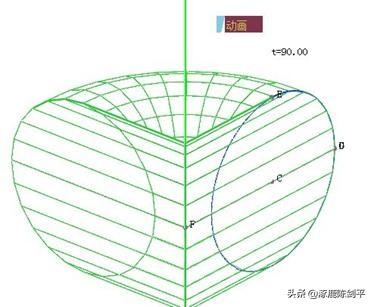
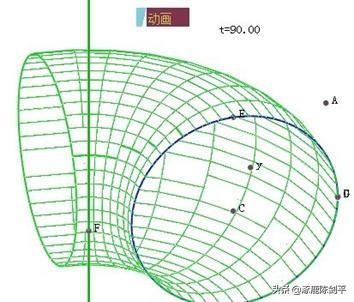
改变平行线的位置，得可得到不同类型的几何体，如下图

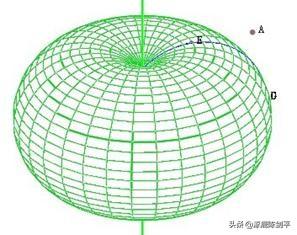
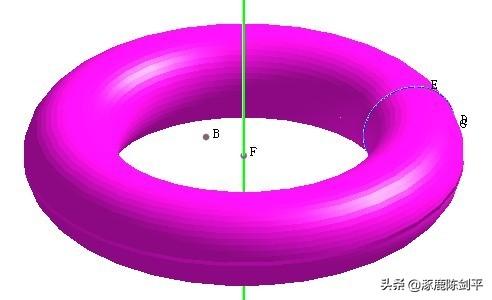
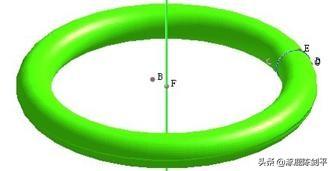
同样方法做出另外的几何体，如下图所示。

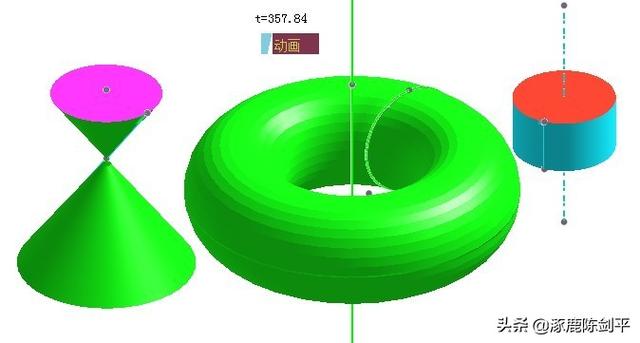
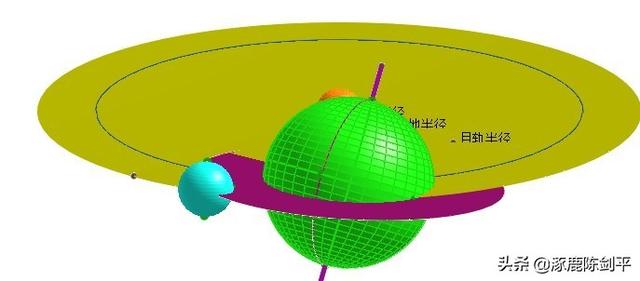
• 立体画板教程 > 课件示例1 >太阳与地球

做法待续：(插图所在文件：15太阳与地琺.chb)

• 立体画板教程 > 课件示例1 >正四面体的展开

做图基本步骤：1 做正三角形，2 做各个边中点和中位线，3 建立一个自由参数，标记该参数为角，4 标记各中位线为旋转轴，旋转顶点，5做出旋转三角形，6 为参数制作动画按钮，动画范围是0-109.

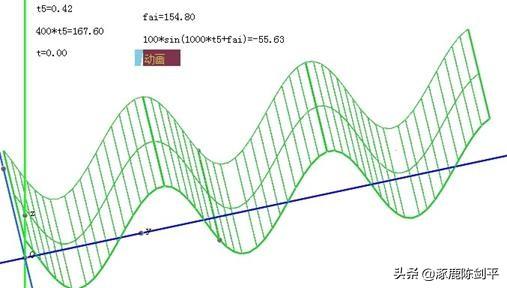
• 立体画板教程 > 课件示例1 >波涛

图形所在文件：16线的轨迹.chb

做法同做线段的轨迹，在6.4做线段轨迹的基础上，新建一个参数fai，把计算参数：400*sin(1000*t)改为：400*sin(1000*t+fai)，并为参数设置一个动画按钮，点击这个按钮则得到波涛的动画。

立体画板 陈剑平