图的存储结构：邻接矩阵 + 邻接表 2 种形式，不同场景下选用其对应的存储结构，这次来聊聊邻接表。
1、稀疏矩阵
有一个稀疏因子，这是节省空间的一种存储方式。
2、邻接表
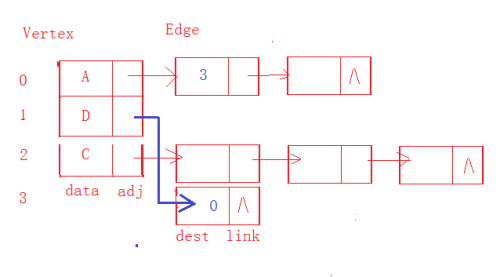
以邻接矩阵存储图结构的话，当实际边数远远小于图的最大边数时，将会存储很多0，势必造成存储空间的巨大浪费；这时，就必须将邻接矩阵该用为邻接表；将邻接矩阵各行组织为一个单链表，类哈希的存储结构。
存储结构(控制头)：
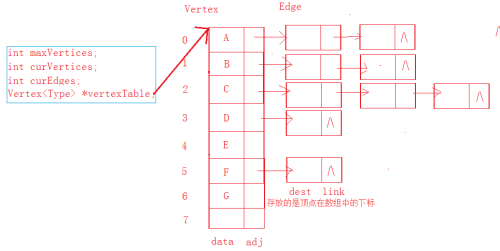3、核心方法
均由C++实现，无向图的邻接表；
(1)、删除边(是链表的删除操作，相对简单)：
推荐阅读：
从零开始学习数据结构-->入门篇
从零开始学习数据结构-->链表
从零开始学习数据结构-->线性表
从零开始学习数据结构-->栈
从零开始学习数据结构-->队列
从零开始学习数据结构-->矩阵+串
从零开始学习数据结构-->哈希表
从零开始学习数据结构-->散列桶
从零开始学习数据结构-->二叉树
1int maxVertices; //最大顶点数
2int curVertices; //当前顶点数
3int curEdges; //当前边数
4
5template<typename Type>
6class Edge{ //边的存储结构
7public:
8 Edge(int num) : dest(num), link(NULL){}
9public:
10 int dest; //是另一个顶点的下标
11 Edge *link;
12};
13template<typename Type>
14class Vertex{ //顶点的存储结构
15public:
16 Type data; //存放的顶点
17 Edge *adj;18};1920Vertex *vertexTable; //指向顶点的指针，是申请数组用的 1bool removeEdge(const Type &v1, const Type &v2){ //删除边
2 int i = getVertexIndex(v1);
3 int j = getVertexIndex(v2);
4
5
6 if(i==-1 || j==-1){ //保证顶点的保存在
7 return false;
8 }
9 //v1-->v2
10 Edge *p = vertexTable[i].adj;11 if(p == NULL){ //判断有没有边12 return false;13 }1415 if(p->link == NULL && p->dest == j){ //删除的是第一个边，其后没有边了；16 vertexTable[i].adj = NULL;17 delete p; 18 }else if(p->dest == j){ //删除的是第一个边,并且其后还有边19 vertexTable[i].adj = p->link;20 delete p;21 }else{22 while(p->link != NULL){23 if(p->link->dest == j){24 Edge *q = p->link;25 p->link = q->link;26 delete q;27 }28 p = p->link;29 }30 }31 //v2-->v132 Edge *s = vertexTable[j].adj;33 if(s == NULL){ //判断有没有边34 return false;35 }3637 if(s->link == NULL && s->dest == i){ //删除的是第一个边，其后没有边了；38 vertexTable[j].adj = NULL;39 delete s;40 curEdges--;41 return false;42 }else if(s->dest == i){ //删除的是第一个边,并且其后还有边43 vertexTable[j].adj = s->link;44 delete s;45 curEdges--;46 return true;47 }else{48 while(s->link != NULL){49 if(s->link->dest == i){50 Edge *q = s->link;51 s->link = q->link;52 delete q;53 curEdges--;54 return true;55 }56 s = s->link;57 }58 }5960 return true;61} 1bool removeVertex(const Type &v){ //删除顶点
2 int i = getVertexIndex(v);
3 if(i == -1){
4 return false;
5 }
6
7 Edge *p = vertexTable[i].adj; //先删除边上的dest和此边 8 while(p != NULL){ 9 vertexTable[i].adj = p->link;10 int k = p->dest;11 Edge *q = vertexTable[k].adj;12 if(q->dest == i){13 vertexTable[k].adj = q->link;14 delete q;15 }else{16 while(q->link != NULL && q->link->dest != i){17 q = q->link;18 }19 Edge *t = q->link;20 q->link = t->link;21 delete t;22 }23 delete p;24 p = vertexTable[i].adj;25 curEdges--;26 }2728 curVertices--; //下面实行覆盖，指针和最后的那个顶点的adj相等;29 vertexTable[i].data = vertexTable[curVertices].data;30 vertexTable[i].adj = vertexTable[curVertices].adj;31 vertexTable[curVertices].adj = NULL;3233 int k = curVertices;34 p = vertexTable[i].adj;35 while(p != NULL){ //修改其它顶点的dest.36 Edge *s = vertexTable[p->dest].adj;37 while(s != NULL){38 if(s->dest == k){39 s->dest = i;40 break;41 }42 s = s->link;43 }44 p = p->link;45 }46 return true;47} 1#ifndef _GRAPH_H_
2#define _GRAPH_H_
3
4#include
5using namespace std;
6
7#define VERTEX_DEFAULT_SIZE 10
8
9template<typename Type>
10class Graph{
11public:
12 bool isEmpty()const{
13 return curVertices == 0;
14 }
15 bool isFull()const{
16 if(curVertices >= maxVertices || curEdges >= curVertices*(curVertices-1)/2)
17 return true; //图满有2种情况：(1)、当前顶点数超过了最大顶点数，存放顶点的空间已满
18 return false; //(2)、当前顶点数并没有满，但是当前顶点所能达到的边数已满
19 }
20 int getCurVertex()const{
21 return curVertices;
22 }
23 int getCurEdge()const{
24 return curEdges;
25 }
26public:
27 virtual bool insertVertex(const Type &v) = 0; //插入顶点
28 virtual bool insertEdge(const Type &v1, const Type &v2) = 0; //插入边
29 virtual bool removeVertex(const Type &v) = 0; //删除顶点
30 virtual bool removeEdge(const Type &v1, const Type &v2) = 0; //删除边
31 virtual int getFirstNeighbor(const Type &v) = 0; //得到第一个相邻顶点
32 virtual int getNextNeighbor(const Type &v, const Type &w) = 0; //得到下一个相邻顶点
33public:
34 virtual int getVertexIndex(const Type &v)const = 0; //得到顶点下标
35 virtual void showGraph()const = 0; //显示图
36protected:
37 int maxVertices; //最大顶点数
38 int curVertices; //当前顶点数
39 int curEdges; //当前边数
40};
41
42template<typename Type>
43class Edge{ //边的存储结构
44public:
45 Edge(int num) : dest(num), link(NULL){}
46public:
47 int dest;
48 Edge *link;
49};
50template<typename Type>
51class Vertex{ //顶点的存储结构
52public:
53 Type data;
54 Edge *adj; 55}; 56template<typename Type> 57class GraphLnk : public Graph{ 58#define maxVertices Graph::maxVertices //因为是模板，所以用父类的数据或方法都得加上作用域限定符 59#define curVertices Graph::curVertices 60#define curEdges Graph::curEdges 61public: 62 GraphLnk(int sz = VERTEX_DEFAULT_SIZE){ 63 maxVertices = sz > VERTEX_DEFAULT_SIZE ? sz : VERTEX_DEFAULT_SIZE; 64 vertexTable = new Vertex[maxVertices]; 65 for(int i = 0; i 66 vertexTable[i].data = 0; 67 vertexTable[i].adj = NULL; 68 } 69 70 curVertices = curEdges = 0; 71 } 72public: 73 bool insertVertex(const Type &v){ 74 if(curVertices >= maxVertices){ 75 return false; 76 } 77 vertexTable[curVertices++].data = v; 78 return true; 79 } 80 bool insertEdge(const Type &v1, const Type &v2){ 81 int v = getVertexIndex(v1); 82 int w = getVertexIndex(v2); 83 84 if(v==-1 || w==-1){ 85 return false; 86 } 87 88 Edge *p = vertexTable[v].adj; 89 while(p != NULL){ //这里主要判断边是否已经存在 90 if(p->dest == w){ //无向图，判断一边即可; 91 return false; 92 } 93 p = p->link; 94 } 95 //v1-->v2 //采用头插 96 Edge *s = new Edge(w); 97 s->link = vertexTable[v].adj; 98 vertexTable[v].adj = s; 99100 //v2-->v1 //采用头插101 Edge *q = new Edge(v);102 q->link = vertexTable[w].adj;103 vertexTable[w].adj = q;104105 curEdges++;106 return true;107 }108 bool removeVertex(const Type &v){109 int i = getVertexIndex(v);110 if(i == -1){111 return false;112 }113114 Edge *p = vertexTable[i].adj;115 while(p != NULL){116 vertexTable[i].adj = p->link;117 int k = p->dest;118 Edge *q = vertexTable[k].adj;119 if(q->dest == i){120 vertexTable[k].adj = q->link;121 delete q;122 }else{123 while(q->link != NULL && q->link->dest != i){124 q = q->link;125 }126 Edge *t = q->link;127 q->link = t->link;128 delete t;129 }130 delete p;131 p = vertexTable[i].adj;132 curEdges--;133 }134135 curVertices--; //下面实行覆盖136 vertexTable[i].data = vertexTable[curVertices].data;137 vertexTable[i].adj = vertexTable[curVertices].adj;138 vertexTable[curVertices].adj = NULL;139140 int k = curVertices;141 p = vertexTable[i].adj;142 while(p != NULL){143 Edge *s = vertexTable[p->dest].adj;144 while(s != NULL){145 if(s->dest == k){146 s->dest = i;147 break;148 }149 s = s->link;150 }151 p = p->link;152 }153 return true;154 }155 bool removeEdge(const Type &v1, const Type &v2){156 int i = getVertexIndex(v1);157 int j = getVertexIndex(v2);158159160 if(i==-1 || j==-1){ //保证顶点的保存在161 return false;162 }163 //v1-->v2164 Edge *p = vertexTable[i].adj;165 if(p == NULL){ //判断有没有边166 return false;167 }168169 if(p->link == NULL && p->dest == j){ //删除的是第一个边，其后没有边了；170 vertexTable[i].adj = NULL;171 delete p; 172 }else if(p->dest == j){ //删除的是第一个边,并且其后还有边173 vertexTable[i].adj = p->link;174 delete p;175 }else{176 while(p->link != NULL){177 if(p->link->dest == j){178 Edge *q = p->link;179 p->link = q->link;180 delete q;181 }182 p = p->link;183 }184 }185 //v2-->v1186 Edge *s = vertexTable[j].adj;187 if(s == NULL){ //判断有没有边188 return false;189 }190191 if(s->link == NULL && s->dest == i){ //删除的是第一个边，其后没有边了；192 vertexTable[j].adj = NULL;193 delete s;194 curEdges--;195 return false;196 }else if(s->dest == i){ //删除的是第一个边,并且其后还有边197 vertexTable[j].adj = s->link;198 delete s;199 curEdges--;200 return true;201 }else{202 while(s->link != NULL){203 if(s->link->dest == i){204 Edge *q = s->link;205 s->link = q->link;206 delete q;207 curEdges--;208 return true;209 }210 s = s->link;211 }212 }213214 return true;215 }216 int getFirstNeighbor(const Type &v){217 int i = getVertexIndex(v);218 if(i != -1){219 Edge *p = vertexTable[i].adj;220 if(p != NULL){221 return p->dest;222 }223 }224225 return -1;226 }227 int getNextNeighbor(const Type &v, const Type &w){228 int i = getVertexIndex(v);229 int j = getVertexIndex(w);230231 if(i==-1 || j==-1){232 return -1;233 }234 Edge *p = vertexTable[i].adj;235 while(p != NULL){236 if(p->dest == j && p->link != NULL){237 return p->link->dest;238 }239 p = p->link;240 }241242 return -1;243 }244public:245 int getVertexIndex(const Type &v)const{246 for(int i = 0; i 247 if(vertexTable[i].data == v){248 return i;249 }250 }251252 return -1;253 }254 void showGraph()const{255 for(int i = 0; i 256 cout<":-->";257 Edge *p = vertexTable[i].adj;258 while(p != NULL){259 cout<dest<<"-->";260 p = p->link;261 }262 cout<<"Nul. "<<endl;263 } 264 }265private:266 Vertex *vertexTable; //指向顶点的指针，是申请数组用的267};268269#endif 1#include"Graph.h"
2
3int main(void){
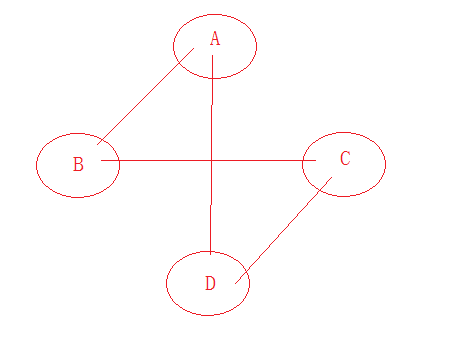
4 GraphLnk<char> gl;
5 gl.insertVertex('A');
6 gl.insertVertex('B');
7 gl.insertVertex('C');
8 gl.insertVertex('D');
9 gl.insertEdge('A','B');
10 gl.insertEdge('A','D');
11 gl.insertEdge('B','C');
12 gl.insertEdge('C','D');
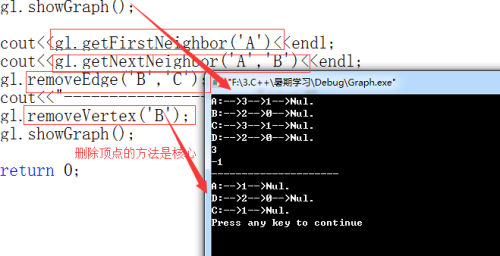
13 gl.showGraph();
14
15 cout<'A')<<endl;16 cout<'A','B')<<endl;17 gl.removeEdge('B','C');18 cout<<"---------------------"<<endl;19 gl.removeVertex('B');20 gl.showGraph();2122 return 0;23}从零开始学习数据结构-->二叉树方法实现
从零开始学习数据结构-->线索二叉树从零开始学习数据结构-->树、森林与二叉树的转换
从零开始学习数据结构-->大堆+小堆
从零开始学习数据结构-->AVL树之旋转算法从零开始学习数据结构-->AVL树之插入算法
从零开始学习数据结构-->AVL树之删除算法 从零开始学习数据结构-->红黑树 从零开始学习数据结构-->图之邻接矩阵 认真的人 自带光芒
扫一扫
7677
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
