奇异方程组的特解用matlab,用列主元消去法分别解方程组Ax=b，用MATLAB程序实现（最有效版）...

数值分析里面经常会涉及到用MATLAB程序实现用列主元消去法分别解方程组Ax=b

具体的方法和代码以如下方程(3x3矩阵)为例进行说明：

用列主元消去法分别解方程组Ax=b，用MATLAB程序实现：

(1)

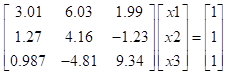
1、 实现该方程的解的MATLAB代码可以分为两种，一种是入门级别的，只是简单地计算出这道题即可，第二种是一种通用的代码，可以实现很多3x3矩阵的方程解，写好以后只需要改不同矩阵里的元素即可算出相应的解，需要建立在对MATLAB比较熟悉的基础上，具体如下：

第一种代码实现—入门级：

A=[3.01,6.03,1.99,;1.27,4.16,-1.23,;0.987,-4.81,9.34]

A1=[3.01,6.03,1.99,1;1.27,4.16,-1.23,1;0.987,-4.81,9.34,1]

B1=A1(1,1:4)

C1=A1(2,1:4)

D1=A1(3,1:4)

E1=-1.27/3.01*B1+C1

F1=-0.987/3.01*B1+D1

p1=E1(1,2)

q1=F1(1,2)

if (abs(p1)>=abs(q1))

a1=p1

a2=q1

FF1=E1

EE1=F1

else

a1=q1

a2=p1

FF1=F1

EE1=E1

end

G1=-a2/a1*FF1+EE1

H1=[E11;FF1;G1]

J1=H1(1:3,1:3)

b1=H1(1:3,4)

x1=J1\b1

第二种代码实现如下—熟练通用级：

A=[3.01,6.03,1.99,;1.27,4.16,-1.23,;0.987,-4.81,9.34]

A1=[3.01,6.03,1.99,1;1.27,4.16,-1.23,1;0.987,-4.81,9.34,1]

B1=A1(1,1:4)

C1=A1(2,1:4)

D1=A1(3,1:4)

f1=A1(1,1)

f2=A1(2,1)

f3=A1(3,1)

if (abs(f1)>=abs(f2))

if(abs(f1)>=abs(f3))

f11=f1

E11=B1

f22=f2

E12=C1

f33=f3

E13=D1

else

f11=f3

E11=D1

f22=f1

E12=B1

f33=f2

E13=C1

end

end

if(abs(e2)>=a