linux 下 qserialport waitforreadyread_北师大版初中数学八年级（下）第一章第四节角平分线（精品）...

第一章 三角形的证明

1.4角平分线

一、知识点梳理

1.角平分线性质定理：

①角平分线平分已知角

②角平分线上的点到这个角两边的距离相等

2.角平分线判定定理：

在一个角的内部，到角的两边距离相等的点在这个角的平分线上

3.作图要求：掌握尺规作图做已知角的角平分线

二、经典题型总结

题型一：利用角平分线的性质证明线段相等

题型二：利用角平分线的性质求线段的长

题型三：利用角平分线的性质定理进行角平分线的判定

题型四：利用角平分线的性质解决实际问题

三、解题技巧点睛

1.当题目中出现“角平分线”时马上想到角平分线的两条性质，一定会用到

2.在角平分线的题目中如果出现平行线，则定会涉及到等腰三角形

3.三角形中两个底角平分线的交角与顶角的关系

三角形中两个底角外角平分线的交角与顶角的关系公式：

四、易错点分析

五、中考真题再现

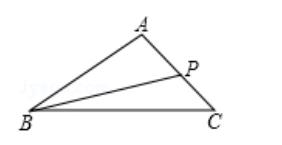
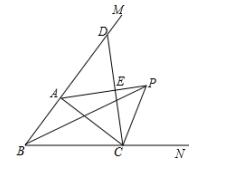
(2019.甘肃.20题)如图，在△ABC中，点P是AC上一点，连接BP，求作一点M，使得点M到AB和AC两边的距离相等，并且到点B和点P的距离相等．(不写作法，保留作图痕迹)

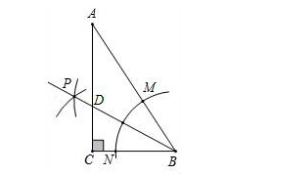
(2019.宁夏.15题)如图，在Rt△ABC中，∠C＝90°，以顶点B为圆心，适当长度为半径画弧，分别交AB，BC于点M，N，再分别以点M，N为圆心，大于MN的长为半径画弧，两弧交于点P，作射线BP交AC于点D．若∠A＝30°，则＝　 　．

六、习题巩固训练

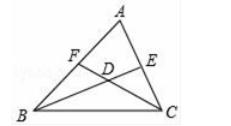
1.如图，BE、CF是△ABC的角平分线，∠A=50°，BE、CF相交于D，则∠BDC的度数是　 　．

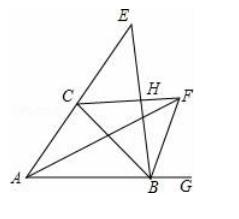
2.已知如图，∠GBC，∠BAC的平分线相交于点F，BE⊥CF于H，若∠AFB＝40°，∠BCF的度数为　 　．

3.如图所示，若AB∥CD，AP、CP分别平分∠BAC和∠ACD，PE⊥AC于点E，PE＝6，则AB与CD之间的距离为　 　．

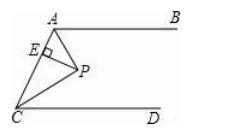
4.如图，已知P是∠AOB的角平分线上的一点，∠AOB＝60°，PD⊥OA，M是OP的中点，点C是OB上的一个动点，若PC的最小值为3cm，则MD的长度为　 　．

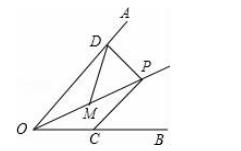
5.如图，BD是△ABC的外角∠ABP的角平分线，DA＝DC，DE⊥BP于点E，若AB＝5，BC＝3，则BE的长为　 　．

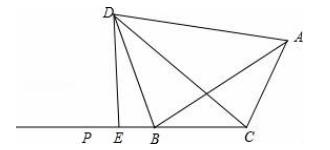
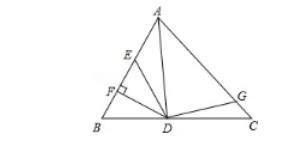
6.如图，AD是△ABC的角平分线，DF⊥AB，垂足为F，DE=DG，△ADG和△AED的面积分别为60和35，则△EDF的面积为　 　．

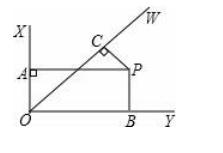
7.如图，∠XOY＝90°，OW平分∠XOY，PA⊥OX，PB⊥OY，PC⊥OW，其中A，B，C为垂足，若OA+OB+OC＝1，则OC＝　 　．

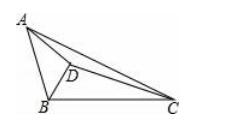
8.如图，三角形ABC中，BD平分∠ABC，AD垂直于BD，三角形BCD的面积为45，三角形ADC的面积为20，则三角形ABD的面积等于　 　．

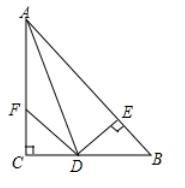
9.如图：在△ABC中，∠C=90°，AD是∠BAC的平分线，DE⊥AB于E，F在AC上，BD=DF，BC=8，AB=10，则△FCD的面积为__________．

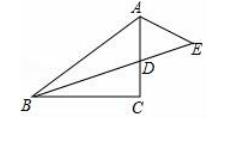
10.如图，在Rt△ABC中，∠C＝90°，AC＝3，BC＝4，∠ABC的平分线交边AC于点D，延长BD至点E，且BD＝2DE，连接AE．

(1)求线段CD的长；

(2)求△ADE的面积．

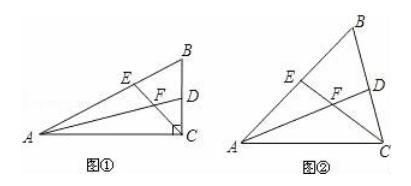
11.如图，在△ABC中，∠ABC的平分线与∠ACB的外角的平分线相交于点P，连接AP．

(1)求证：PA平分∠BAC的外角∠CAM；

(2)过点C作CE⊥AP，E是垂足，并延长CE交BM于点D．求证：CE＝ED．

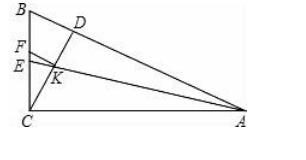
12.如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB于D，AE平分∠BAC，交CD于K，交BC于E，F是BE上一点，且BF＝CE，

求证：FK∥AB．

13.如图，在Rt△ABC中，∠C＝90°，AC＝3，BC＝4，∠ABC的平分线交边AC于点D，延长BD至点E，且BD＝2DE，连接AE．

(1)求线段CD的长；

(2)求△ADE的面积．

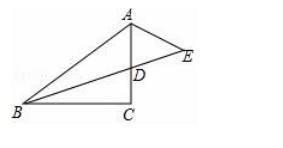
14.在Rt△ABC中，∠ACB＝90°，∠B＝60°，AD、CE分别是∠BAC、∠BCA的平分线，AD、CE相交于点F，

①请你判断并写出FE与FD之间的数量关系．

②如果∠ACB不是直角，其他条件不变，①中所得结论是否仍然成立？若成立，请证明；若不成立，请说明理由．

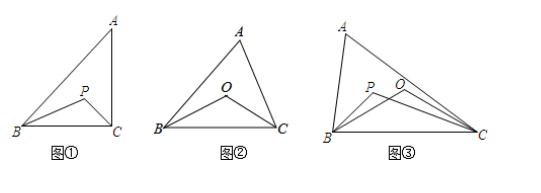
15.已知：△ABC是三边都不相等的三角形，点O和点P是这个三角形内部两点．

(1)如图①，如果点P是这个三角形三个内角平分线的交点，那么∠BPC和∠BAC有怎样的数量关系？请说明理由；

(2)如图②，如果点O是这个三角形三边垂直平分线的交点，那么∠BOC和∠BAC有怎样的数量关系？请说明理由；

(3)如图③，如果点P(三角形三个内角平分线的交点)，点O(三角形三边垂直平分线的交点)同时在不等边△ABC的内部，那么∠BPC和∠BOC有怎样的数量关系？请直接回答．

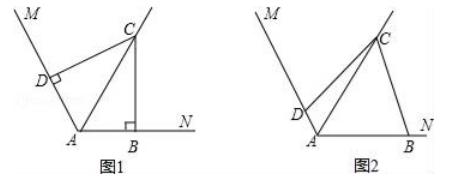
16.已知∠MAN=120°，AC平分∠MAN．

(1)在图1中，若∠ABC=∠ADC=90°，求证：AB+AD=AC；

(2)在图2中，若∠ABC+∠ADC=180°，则(1)中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由．