小学阶段采用的是将任意一个三角形的三个内角，拼接在一起形成一条直线，根据这个事实得出任意三角形的内角和是180度的结论。到初中学了平行线的特性之后，就可以很严谨地证明这个结论。在小学只需要知道这个结论就行。
根据这个结论知道两个内角的度数，可求出第三个内角的度数。
虽然三角形只有三个内角，但任意一个三角形至少有两个内角是锐角。也就是说一个三角形中，最多只有一个直角，因为两个直角就是180度了，第三个角都没有了，所以不可能存在这种情况。或最多一个钝角，它比直角的度数还大，更不可能有两个钝角。
有两种三角形是比较特殊的。一种是等边三角形也称为正三角形。当我们看到正三角形，我们的第一反应是什么？三条边完全相等，而且三个内角每个都是60度。也就是相当于告诉了我们各个角的度数。
等腰直角三角形，因为三角形的内角和是180度，而且我们知道一个角是直角，根据等边对等角，所以说另外两个角均为45度。
在做题过程中看到135度或45度，头脑中要闪过一个念头，如果添加一条辅助线，是否有可能转化成等腰直角三角形。
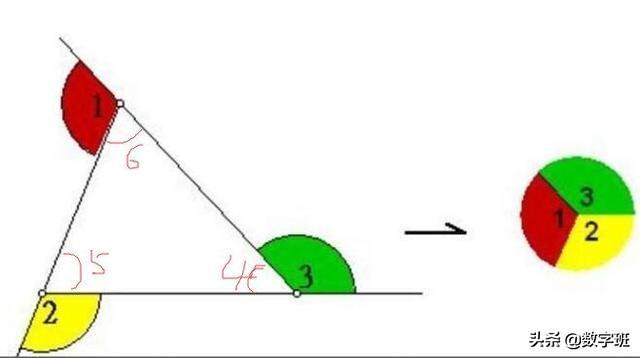
角3与角4互补
在三角形的角度问题当中，外角与它相邻的内角和等于180度。因此外角也就等于与它不相邻的两个内角的和。这个在解题过程中经常会用到。
在三角形中，内角度数有大小的区别，边长有长短之分。但并不是随便三条线段都能围成三角形的。在同一个三角形内，三条边的长度关系是有一定限制范围的。在一个三角形中任意两条边之和大于第三边，任意两边之差小于第三边。这个也是三条线段能否围成一个三角形的必要条件之一。
在同一个三角形内有等边对等角的规律。最特殊的情况就是三条边长一样长的情况，也就是大家熟悉的正三角形。
我们看一道简单的练习题。
已知一个三角形的一条边长为3厘米，另外一条边长为5厘米，问这个三角形的边长L在什么范围？
分析：因为是取值范围，所以说答案不是一个固定的数。
这个取值范围怎么算呢？这个就需要根据构成三角形的三条边的长度关系来计算。根据任意两边之和大于第三边，任意两边之差小于第三边。
5-3=2(厘米)；5+3=8(厘米)。
也就是说这一条边长的范围是大于2厘米且小于8厘米。根据三角形的周长等于三条边长的和。
所以：10厘米
扫一扫
119
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
