networkx 点的属性_python图算法库Networkx笔记-第一章

基础操作：

import networkx as nx
import matplotlib.pyplot as plt

%matplotlib inline 


# 创建一个graph object
G  = nx.Graph()

# 添加一个节点
G.add_node('A')

# 通过列表添加节点
G.add_nodes_from(['B','C'])

# 添加一条边
G.add_edge('A','B')

# 通过列表添加多条边
G.add_edges_from([('B','C'),('A','C')])


# 把图画出来
plt.figure(figsize=(7.5,7.5))

# 使用对象G作为画像
nx.draw_networkx(G)
plt.show()

# 这里出来的图可能不一样，可以使用random.seed固定
import random
from numpy import random as nprand

seed = hash("asdads") % 2**32
nprand.seed(seed)
random.seed(seed)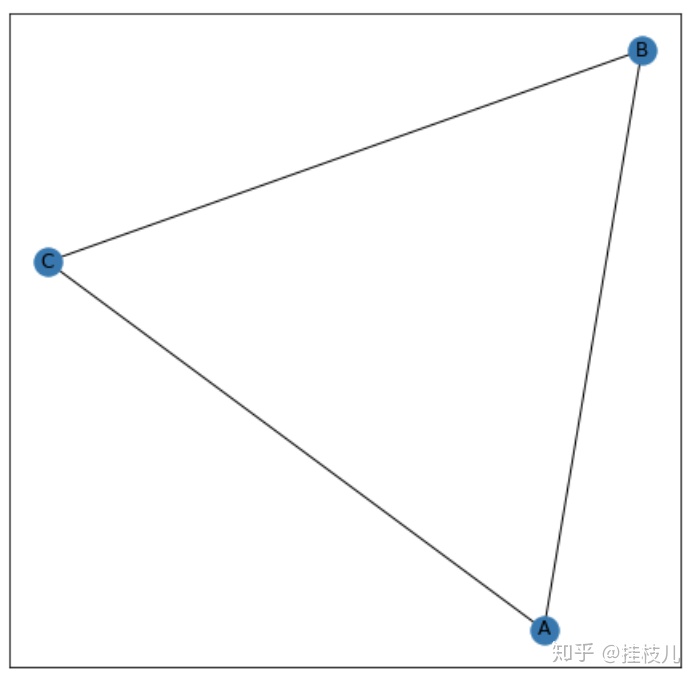

# 再加2个节点
plt.figure(figsize=(7.5,7.5))
G.add_edges_from([('B','D'),('C','E')])
nx.draw_networkx(G)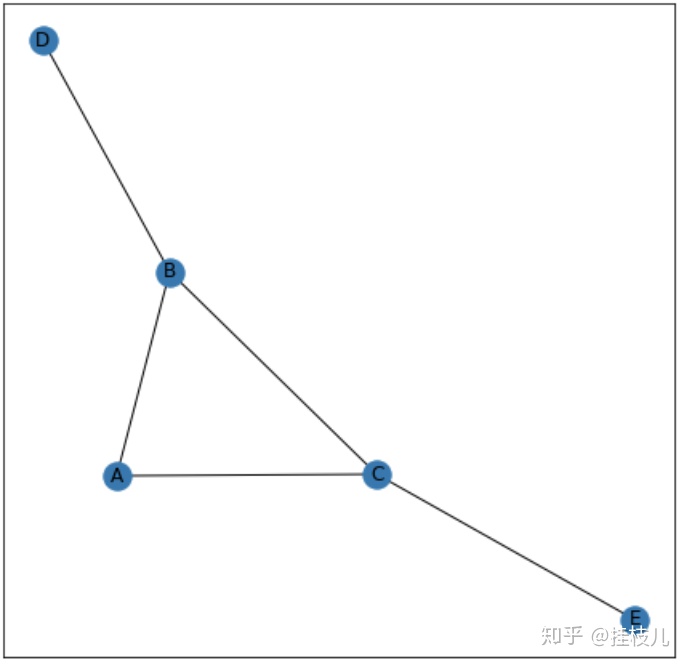

开始把玩Networkx

我们将会开始熟悉一下概念：

• Graph类
• 节点的Attributes
• 遍的权重Edge Weights
• 有向图DiGraph Class
• 平行边MultiGraph and MultiDiGraph

Graph类

• 我们使用karate_clb_graph()来帮助理解

plt.figure(figsize=(8,8))
G = nx.karate_club_graph()
# 尝试把连起来的点连接到一起
karate_pos = nx.spring_layout(G,k=0.05)
nx.draw_networkx(G,karate_pos)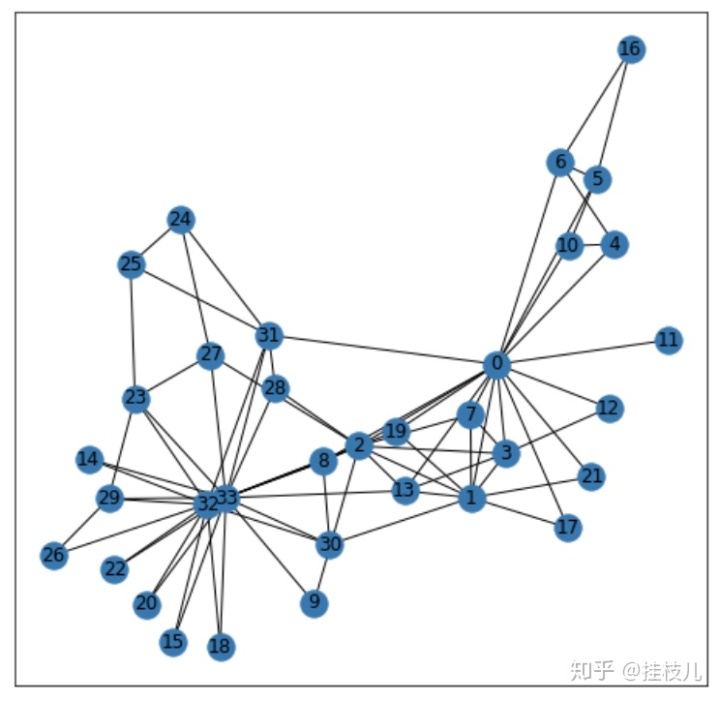

我们可以通过Graph类直接访问节点和边属性

print(list(G.nodes))

>>> 
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33]

print(G.edges)

>>>
[(0, 1), (0, 2), (0, 3), (0, 4), (0, 5), (0, 6), (0, 7), (0, 8), (0, 10), (0, 11), (0, 12), (0, 13), (0, 17), (0, 19), (0, 21), (0, 31), (1, 2), (1, 3), (1, 7), (1, 13), (1, 17), (1, 19), (1, 21), (1, 30), (2, 3), (2, 7), (2, 8), (2, 9), (2, 13), (2, 27), (2, 28), (2, 32), (3, 7), (3, 12), (3, 13), (4, 6), (4, 10), (5, 6), (5, 10), (5, 16), (6, 16), (8, 30), (8, 32), (8, 33), (9, 33), (13, 33), (14, 32), (14, 33), (15, 32), (15, 33), (18, 32), (18, 33), (19, 33), (20, 32), (20, 33), (22, 32), (22, 33), (23, 25), (23, 27), (23, 29), (23, 32), (23, 33), (24, 25), (24, 27), (24, 31), (25, 31), (26, 29), (26, 33), (27, 33), (28, 31), (28, 33), (29, 32), (29, 33), (30, 32), (30, 33), (31, 32), (31, 33), (32, 33)]

我们可以通过节点的索引查看某个节点是否在图上

G.has_node(0)

>>> True

除了单节点的情况，我们也可以输入某一个节点，得到这个节点的临边节点

list(G.neighbors(0))

>>>
[1, 2, 3, 4, 5, 6, 7, 8, 10, 11, 12, 13, 17, 19, 21, 31]

一样的，看某条边在图上是否存在

(0,1)in G.edges

向图中的点加入ID属性

Graph属性支持向节点加入任何类型的属性。对于一个节点，他们的节点属性都存储在了G.nodes[v],v就是节点的id。我们可以利用这个属性把节点分为2类

member_club = [ 
    0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 
    0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 
    1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 
    1, 1, 1, 1]

for node_id in G.nodes:
    G.nodes[node_id]['club'] = member_club[node_id]

# 也可以通过手动的方式在加入节点的时候输入额外的属性
G.add_node(11,club=0)

G.nodes[0]
>>> {'club': 0}

我们可以通过颜色标签对图标进行进一步的可视化

node_colors = [
    '#1f78b4' if G.nodes[v]['club'] == 0 else '#33a02c' for v in G
]

plt.figure(figsize=(15,8))
nx.draw_networkx(G,karate_pos,label=True,node_color=node_colors)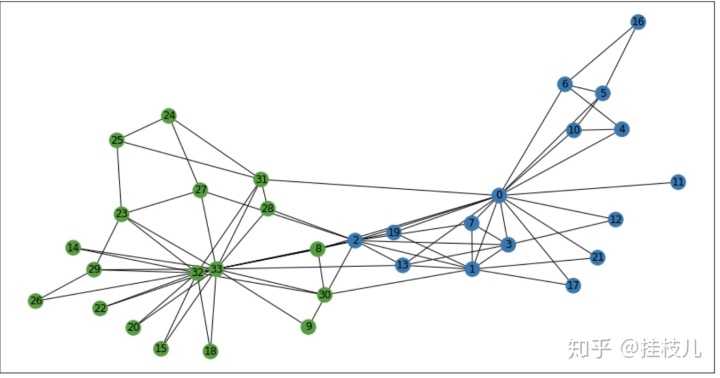

对于边，我们也可以加入属性，比如我们针对边加入是否属于一个club的属性，同时我们还可以根据属性来选择节点

for v,w in G.edges:
    if G.nodes[v]['club'] == G.nodes[w]['club']:
        G.edges[v,w]['internal'] = True
    else:
        G.edges[v,w]['internal'] = False


internal = [e for e in G.edges if G.edges[e]['internal']]
external = [e for e in G.edges if ~G.edges[e]['internal']]

我们可以根据目前得到的属性来进一步可视化我们的关系网络。但是注意一次性只支持画一种Linestyle,所以我们分2次画完。

plt.figure(figsize=(12,7))
nx.draw_networkx_nodes(G,karate_pos,node_color=node_colors)
nx.draw_networkx_labels(G,karate_pos)

# 然后分别画同类边和不同类边2种节点

nx.draw_networkx_edges(G,karate_pos,edgelist=internal)
nx.draw_networkx_edges(G,karate_pos,edgelist=external,style='dashed')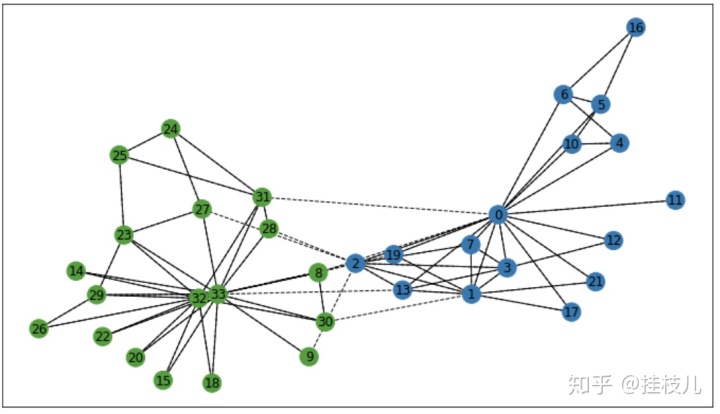

向边添加权重属性

边的权重对于节点的连接存在不同的强弱的时候特别有用。比如，2个好友的通话频率？2个城市间的航班频率等。虽然实力的club图没有这种节点，但我们可以衍生出一种Tie Strength的概念。连接属性随着2个节点的共同邻居数增长而增长。下面提供一个函数来计算连接权重：

def tie_strength(G,v,w):
    
    v_neighbors = set(G.neighbors(v))
    w_neighbors = set(G.neighbors(w))
    
    return 1 + len(v_neighbors & w_neighbors)

# 为什么要+1？  因为权重为0就没有边拉

使用函数对每条边赋予权重

# Calculate weight for each edge 
for v, w in G.edges: 
    G.edges[v, w]["weight"] = tie_strength(G, v, w) 
# Store weights in a list 
edge_weights = [ G.edges[v, w]["weight"] for v, w in G.edges ]

我们可以把边的权重传入spring_layout()函数，来让链接的紧密的点靠的更近一些

weighted_pos = nx.spring_layout(G,pos=karate_pos,k=.3,weight='weight')

最后可视化一个带有权重的图

plt.figure(figsize=(16,7))
nx.draw_networkx( 
    G, weighted_pos, width=8, node_color=node_colors, 
    edge_color=edge_weights, edge_cmap=plt.cm.Blues,
    edge_vmin=0, edge_vmax=6) 
 # Draw solid/dashed lines on top of internal/external edges 
nx.draw_networkx_edges(
    G, weighted_pos, edgelist=internal, edge_color="gray") 
nx.draw_networkx_edges(
    G, weighted_pos, edgelist=external, edge_color="gray", style="dashed")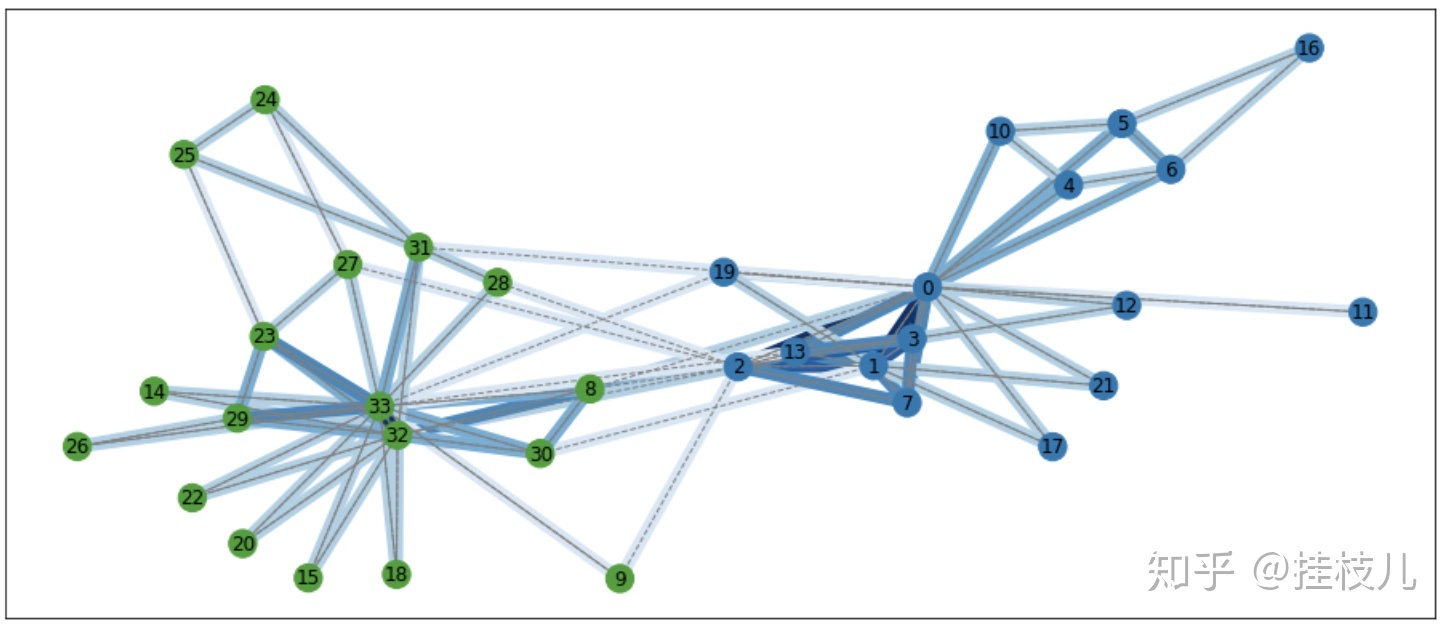

有向图—— when direction matters

这里用了一个另外的例子

G = nx.read_gexf(data)
student_pos = nx.spring_layout(G,k=1.5)
nx.draw_networkx(G,student_pos,arrowsize=20)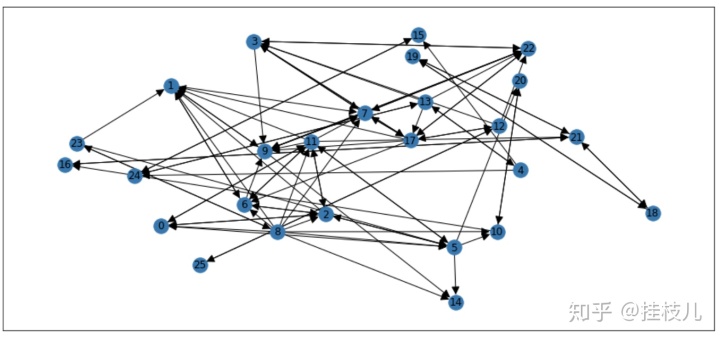

在有向图中，我们有2种临边关系。一个节点可以通过进或出两种节点类型来进行分类。在有向图中调用neighbors()方法会返回他们的向外延展的节点。当然也可以调用successor()方法2者的作用完全一样。同样的我们也可以调用节点的predecessor()方法会返回入度的节点。

[*G.predecessors('0')]
>>>['2', '11', '8']

[*G.successors('0')]
>>>['2', '5', '11']

[*G.neighbors('0')]
>>>['2', '5', '11']

在有向图中，我们可以通过使用in_edges（保证第一个元素是入点)以及out_edges（保证第一个元素是出点），以及，我们可以通过to_undirected()方法把有向图变为无向图，reciprocal=True的话只有有向图中2边都存在的节点才会在无向图中最终出现。下面在代码中画图实现：

G_either = G.to_undirected()
G_both = G.to_undirected(reciprocal=True)

plt.subplot(1,2,1)
nx.draw_networkx(G_either,student_pos)

plt.subplot(1,2,2)
nx.draw_networkx(G_both,student_pos)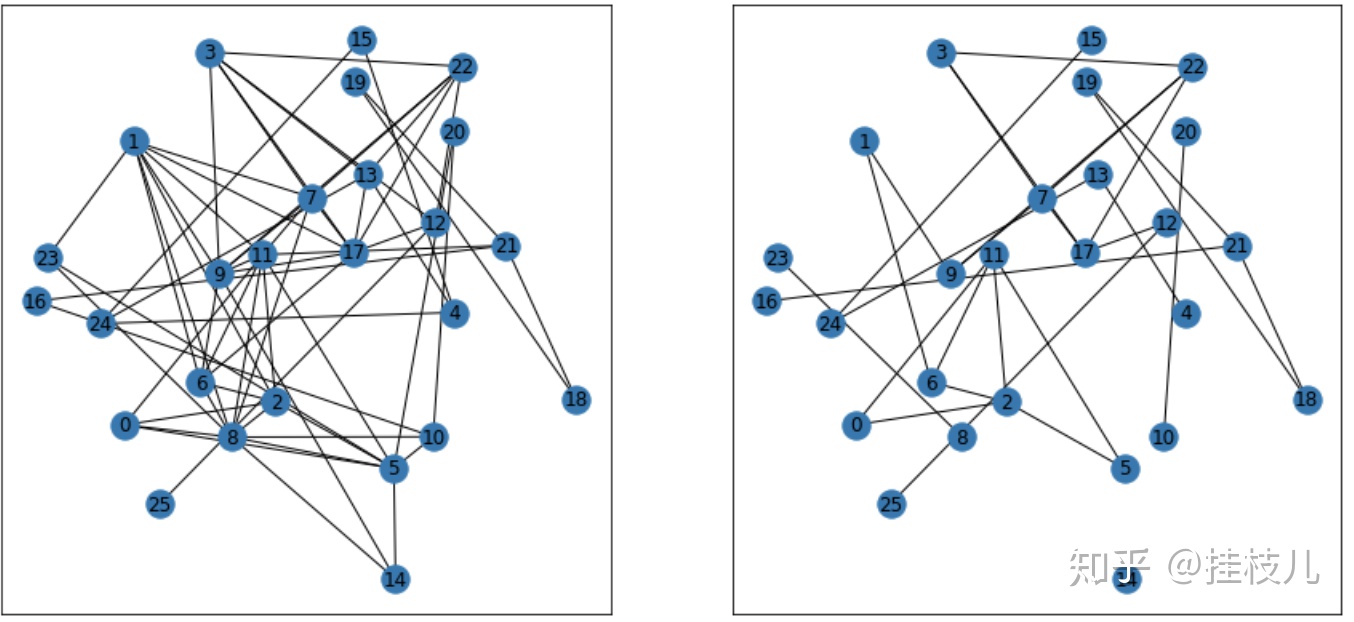

MultiGraph and multiDiGraph

当2个节点有不止一条边时候，我们可以通过MultiGraph和MultiDiGraph类来解决问题

# The seven bridges of Königsberg 
G = nx.MultiGraph() 
G.add_edges_from([ 
    ("North Bank", "Kneiphof", {"bridge": "Krämerbrücke"}), 
    ("North Bank", "Kneiphof", {"bridge": "Schmiedebrücke"}), 
    ("North Bank", "Lomse",    {"bridge": "Holzbrücke"}), 
    ("Lomse",      "Kneiphof", {"bridge": "Dombrücke"}), 
    ("South Bank", "Kneiphof", {"bridge": "Grüne Brücke"}), 
    ("South Bank", "Kneiphof", {"bridge": "Köttelbrücke"}), 
    ("South Bank", "Lomse",    {"bridge": "Hohe Brücke"}) 
])

list(G.edges)
>>>
[('North Bank', 'Kneiphof', 0),
 ('North Bank', 'Kneiphof', 1),
 ('North Bank', 'Lomse', 0),
 ('Kneiphof', 'Lomse', 0),
 ('Kneiphof', 'South Bank', 0),
 ('Kneiphof', 'South Bank', 1),
 ('Lomse', 'South Bank', 0)]