本文详细解析了矢量合成和分解的法则，通过蜡块在浮力作用下在水中运动的实例，介绍了如何建立坐标系，分析蜡块的速度、位移。接着，讨论了合运动与分运动的特性，包括独立性、等时性、等效性和同体性，并通过实例说明了如何进行运动的合成与分解。文章还涉及了小船渡河问题，探讨了最短时间和最短位移的条件，提供了解题步骤和相关例题，帮助读者深入理解运动合成与分解的原理。
小编乱入
/
知知识会识会
知识会0 1 一个平面运动的实例
1. 建立坐标系
如下图所示，为研究密封在玻璃管内水中蜡块的运动，以蜡块开始运动的位置为原点O建立坐标系．
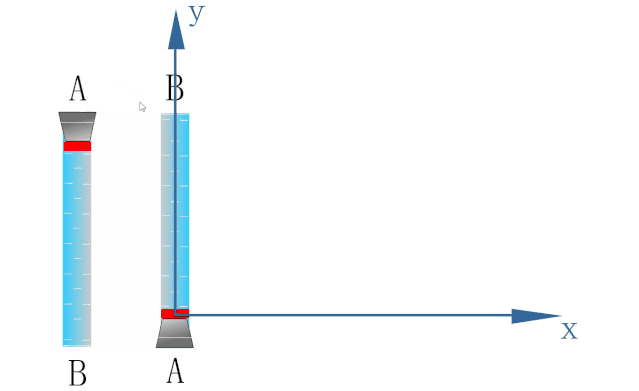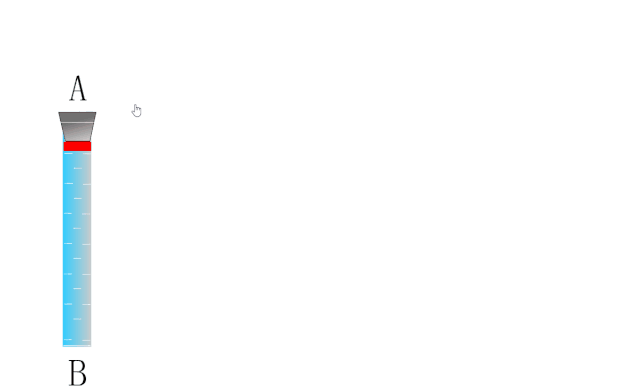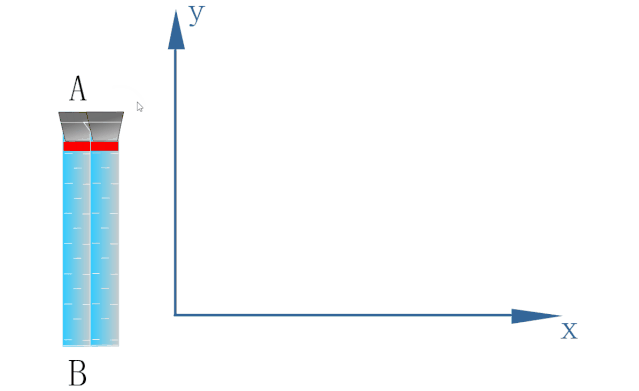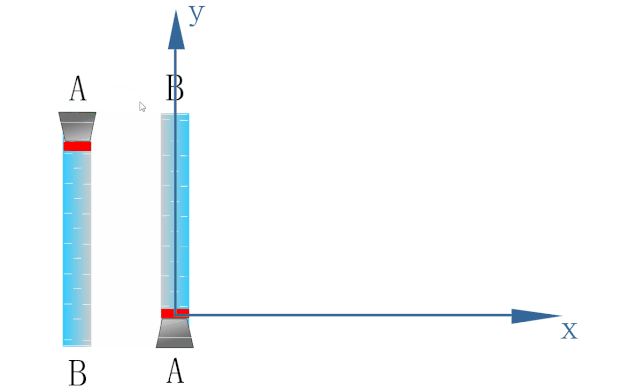
蜡块在浮力的作用下恰能以速度v1沿y轴方向做匀速直线运动．
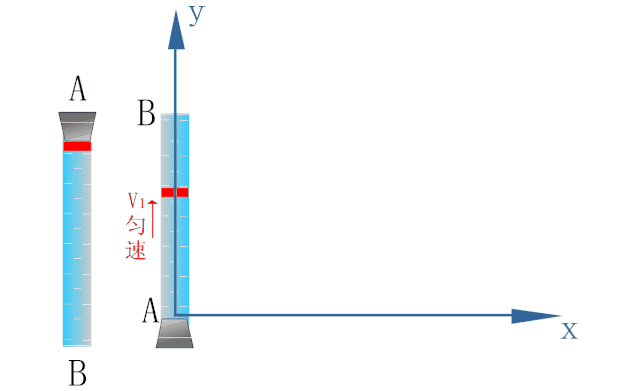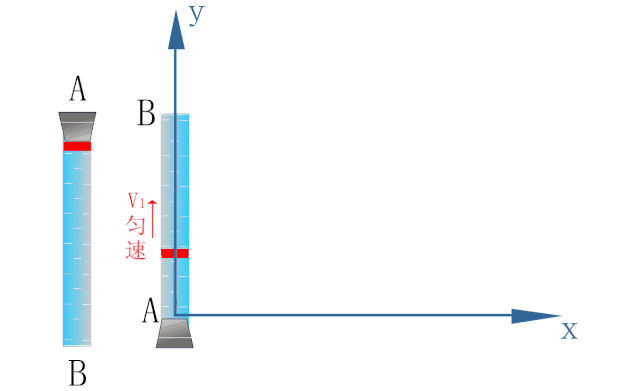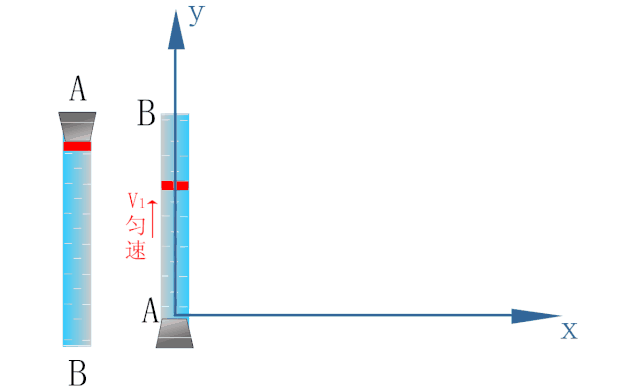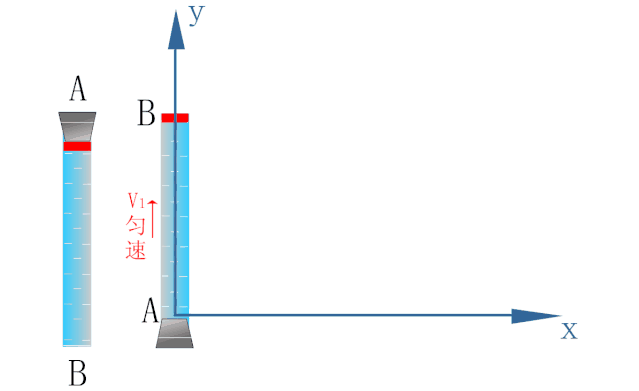
玻璃管能以速度v2沿x轴方向做匀速直线运动．
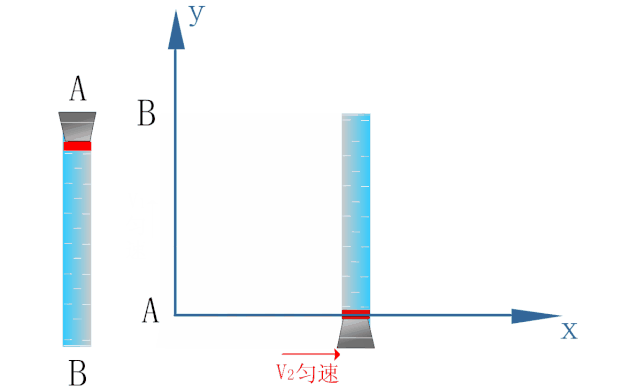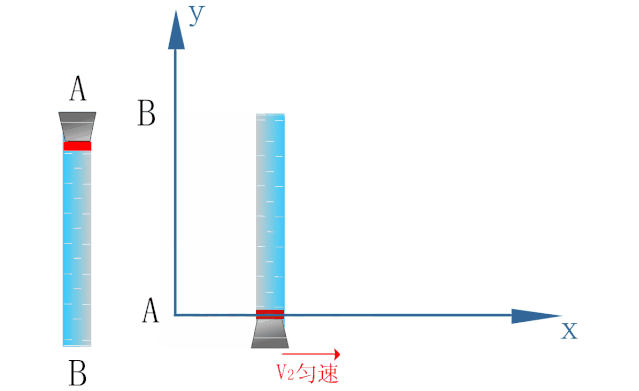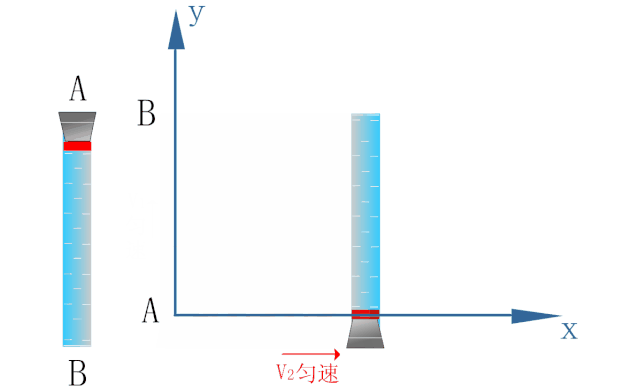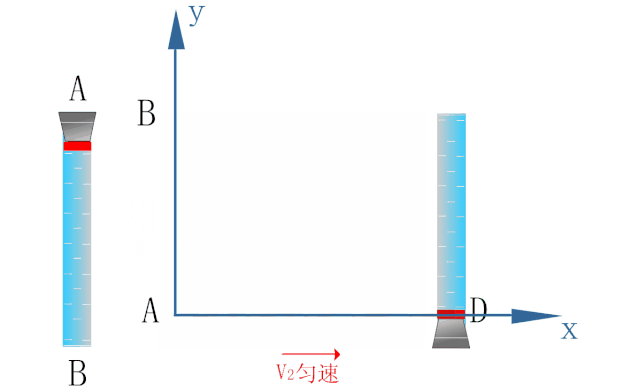
若在玻璃管沿x轴方向做匀速直线运动的同时释放小蜡块，则小蜡块的运动情况如下图所示．
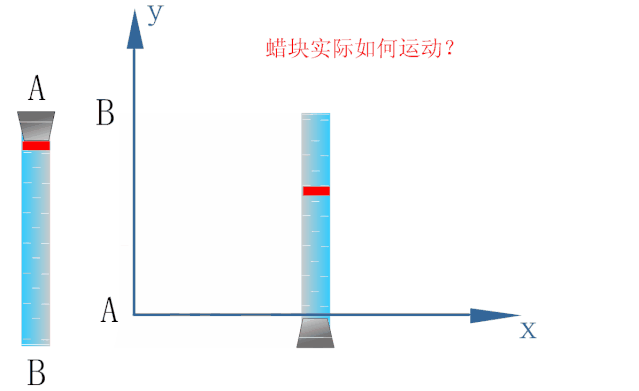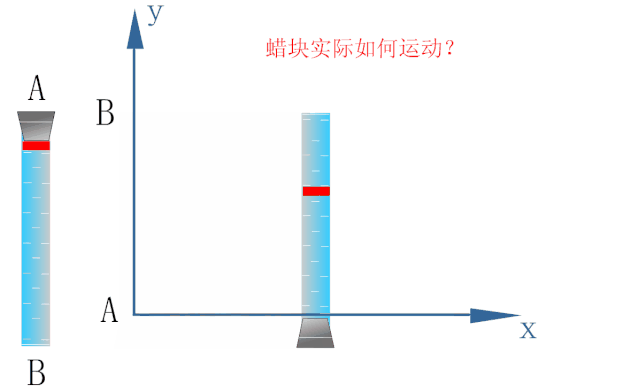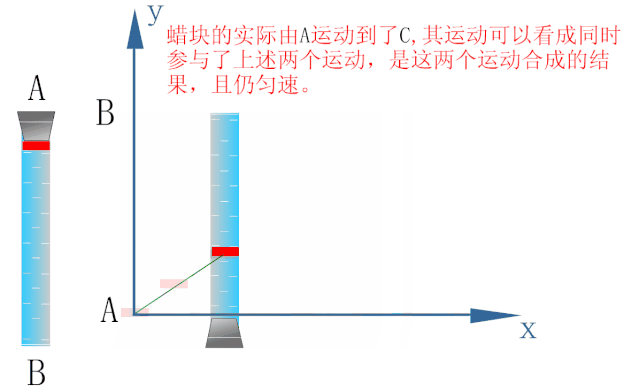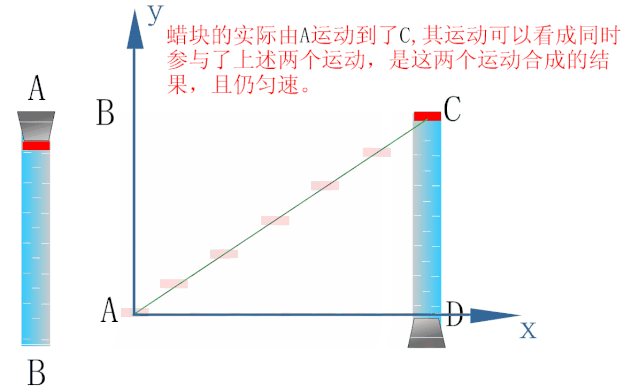
2. 蜡块运动的轨迹
从蜡块开始运动的时刻计时，在某时刻t，蜡块的位置P可以用它的x、y两个坐标表示，即
x＝v2t
y＝v1t
以上两式联立，消掉t，可得
由于v1和v2都是常量(这里说的“常量”，指的是它不随位置、时间变化.)所以
也是常量，可见代表的是一条过原点的直线，这样就用数学语言表达了蜡块的运动轨迹是一条过原点的直线．
3. 蜡块运动的速度、位移
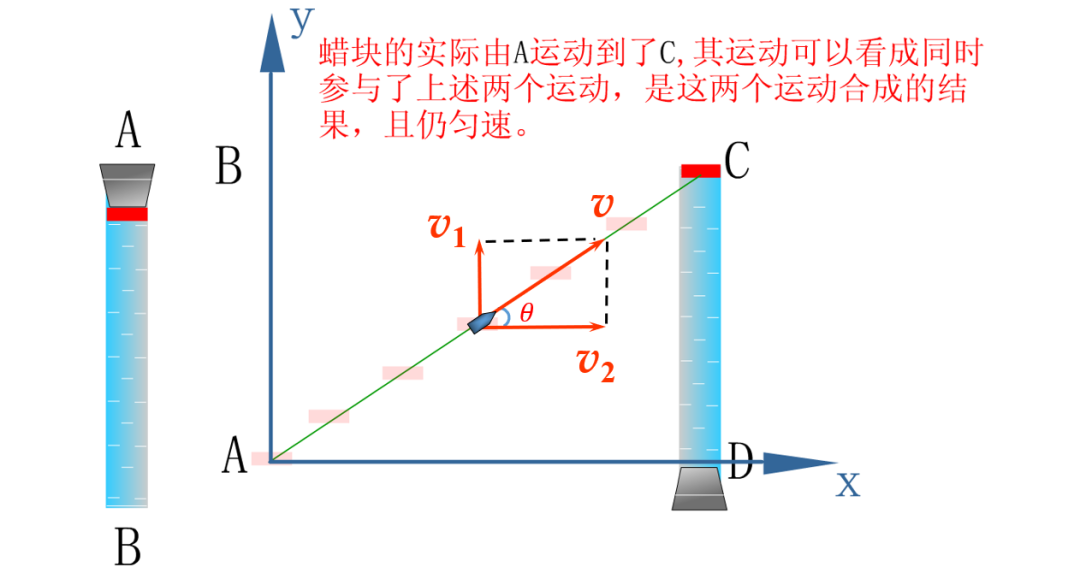
由上图所示，蜡块运动的速度为
方向：tan θ＝
由上图所示，蜡块位移的大小l＝
0 2 运动的合成与分解
如下图所示，在上面的例子中，蜡块沿y轴方向的运动和沿x轴方向的运动都叫作分运动；而蜡块相对于地面实际进行的运动叫作合运动．
由分运动求合运动的过程，叫作 运动的合成 ；由合运动求分运动的过程，叫作 运动的分解 ．运动的合成与分解互为逆运算．
运动的合成与分解遵从 平行四边形 定则或三角形定则．
1. 合运动与分运动的特性
(1)独立性：一个物体同时参与几个分运动，各分运动独立进行，不受其他分运动的影响．
(2)等时性：各分运动经历的时间与合运动经历的时间 相等 ，求物体的运动时间时，可选择一个简单的运动进行求解．
(3)等效性：各分运动叠加起来与合运动有相同的效果，即分运动与合运动可以等效替代．这样为了解题方便，我们就可以根据解题的需要进行运动的合成和分解．
(4)同体性：各分运动与合运动是同一个物体的运动．
运动的合成与分解
实验演示：运动的合成和分解
2. “三步走”求解合运动或分运动
(1)根据题意确定物体的合运动与分运动．
(2)利用“化曲为直”的思想把曲线运动分解为两个方向上的直线运动，根据平行四边形定则作出矢量合成或分解的平行四边形．
(3)根据所画图形求解合运动或分运动的参量，求解时可以利用勾股定理、三角函数等数学知识．
示范例题
例题1.(单选题)关于合运动与分运动，下列说法正确的是( )
A．合运动的速度等于两个分运动的速度之和
B．合运动的时间一定等于分运动的时间
C．两个直线运动的合运动一定是直线运动
D．合运动的速度方向一定与其中某一分速度方向相同
【答案】B
【解析】根据平行四边形定则知，合运动的速度可能比分运 动的速度大，可能比分运动的速度小，可能与分运动的速度 相等，故A错误；
合运动与分运动具有等时性，故B正确；
两个直线运动的合运动不一定是直线运动，故C错误；
合运动的速度方向可能与某一分运动的速度方向相同，也可能不同，故D错误．
K重难
01 两个互成角度的直线运动的合运动
1. 合运动性质的判断
2. 两个互成角度的直线运动的合运动性质的判断
根据合加速度方向和合初速度方向的关系，判定合运动是直线运动还是曲线运动，具体分为以下几种情况：
(1)两个匀速直线运动的合运动一定是 匀速直线 运动．
(2)两个初速度均为零的匀变速直线运动的合运动一定是 初速度为零的匀变速直线运动．
(3)一个匀速直线运动和一个匀变速直线运动的合运动是 匀变速 运动，当二者速度方向共线时为匀变速直线运动，不共线时为匀变速曲线运动．
(4)两个匀变速直线运动的合运动一定是 匀变速 运动．
若两运动的合初速度方向与合加速度方向在同一条直线上，则合运动是匀变速直线运动，如下图所示．
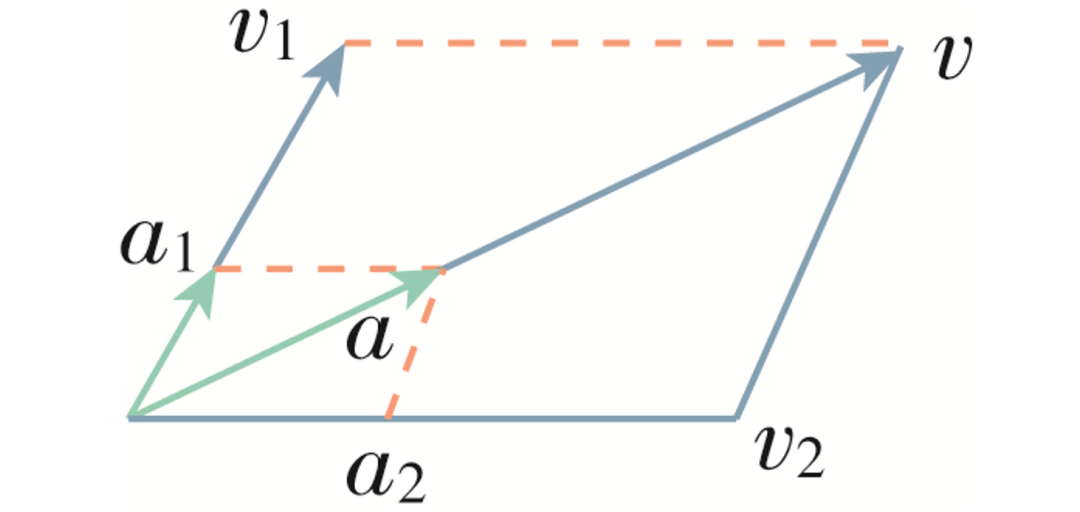
若合初速度方向与合加速度方向不在一条直线上，则合运动是匀变速曲线运动，如下图所示．
两个直线运动的合运动性质的判断
示范例题
例题1.(单选题)关于两个运动的合运动，下列说法中正确的是( )
A．两个直线运动的合运动一定是直线运动
B．两个互成角度的匀速直线运动的合运动一定是匀速直线运动
C．两个互成角度的匀变速直线运动的合运动一定是匀变速直线运动
D．两个分运动的时间和它们的合运动的时间不相等
【答案】B
【解析】两个分运动是直线运动，其合运动不一定是直线运动；两个匀速直线运动的合运动一定是匀速直线运动，故选项B正确，A错误．
两个互成角度的匀变速直线运动，合初速度为v，合加速度为a，由物体做曲线运动的条件可知，当v与a共线时，合运动为匀变速直线运动，当v与a不共线时，合运动为匀变速曲线运动，故选项C错误．
分运动和合运动具有等时性，故选项D错误．
例题2.(单选题)如下图所示，一块橡皮用不可伸长的细线悬挂于O点，用铅笔靠着细线的左侧水平向右匀速移动，运动中始终保持悬线竖直，则橡皮运动的速度( )
A．大小和方向均不变
B．大小不变，方向改变
C．大小改变，方向不变
D．大小和方向均改变
【答案】A
【解析】橡皮参与了两个分运动，一个是沿水平方向与铅笔速度相同的匀速直线运动，另一个是沿竖直方向与铅笔移动速度大小相等的匀速直线运动，这两个直线运动的合运动是斜向上的匀速直线运动，故选项A正确．
点拨
先确定两个分运动，再确定合运动．
(1)橡皮在水平方向做匀速直线运动，在竖直方向也做匀速直线运动．
(2)橡皮的实际运动是两个匀速直线运动的合运动．
0 2 小船渡河问题
1. 小船渡河问题可以基于以下几点进行理解和分析
(1)将船的实际运动看成船随水流的运动和船在静水中的运动的合运动．船的航行方向是实际运动的方向，即合速度的方向．
(2)如下图所示，v水表示水流速度，v静水表示船在静水中的速度，将船在静水中的速度v静水沿平行于河岸和垂直于河岸方向正交分解，则v水－v静水cos θ为船实际上沿水流方向的运动速度，v⊥＝v静水sin θ为船在垂直于河岸方向的运动速度．两个方向的运动情况相互独立、互不影响．
2. 两类渡河问题
2-1 渡河时间最短问题
问题：船在静水中的速度为v船，水流的流速为v水．船怎样行驶才能使过河时间最短呢？最短时间是多少呢？
解决：为船任意选择一个行驶方向进行研究，如下图所示，船头与河岸的夹角为θ．那么，船速可以分解为：用以过河的v1和顺流而下的v2，v1垂直于河岸，v2平行于河岸．
v1=v船sin θ
v2=v船cos θ
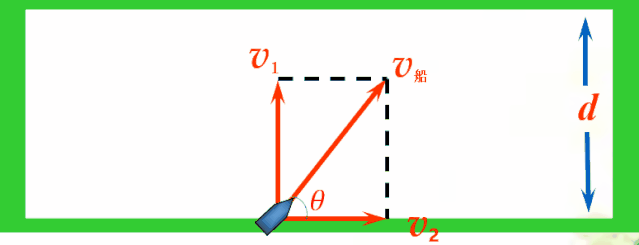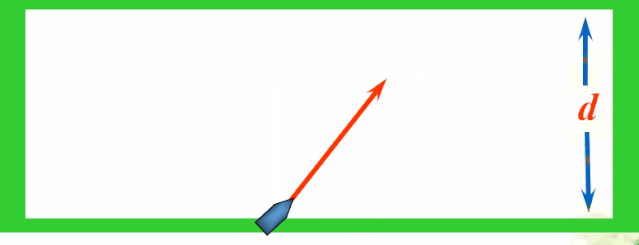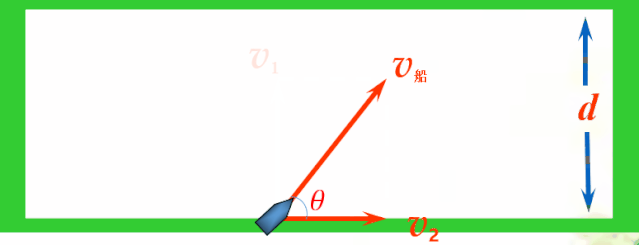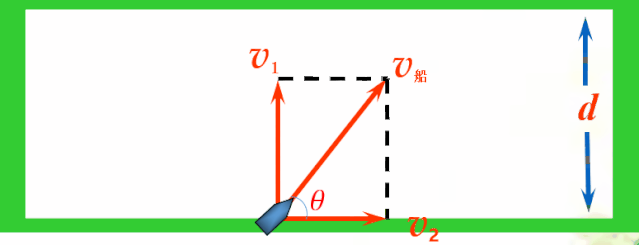
(1)从物理角度分析，顺流而下的速度v2对过河毫无意义，他叠加到水速的效果上，只是使船沿河向下游的速度变大了而已．只有v1才有意义．那么当船头垂直于河岸行驶时，速度就不会浪费了，所以船头应该垂直于河岸行驶．
(2)从数学角度分析，当
时，v1最大，过河时间最短．
以上两种分析方法殊途同归，得到相同的结论：
虽然这样过河时间最短，但是，位移不是最短的哦！小船真实的运动轨迹如下图所示．
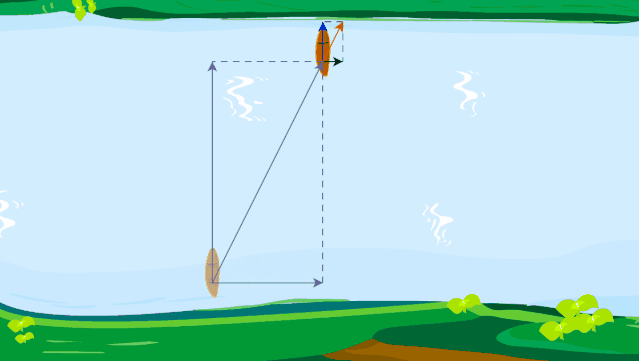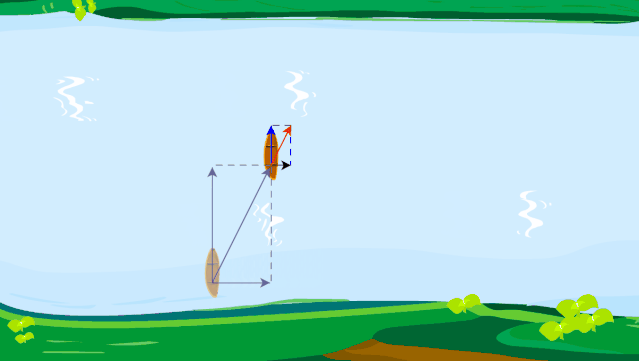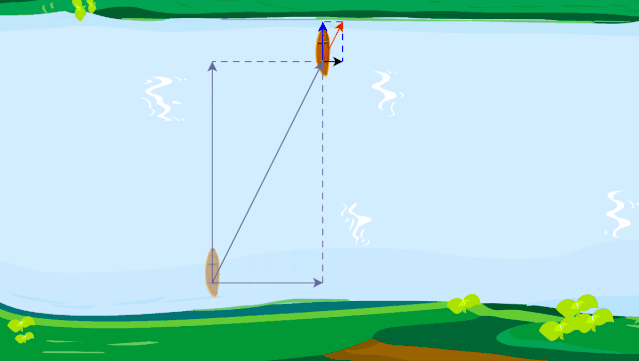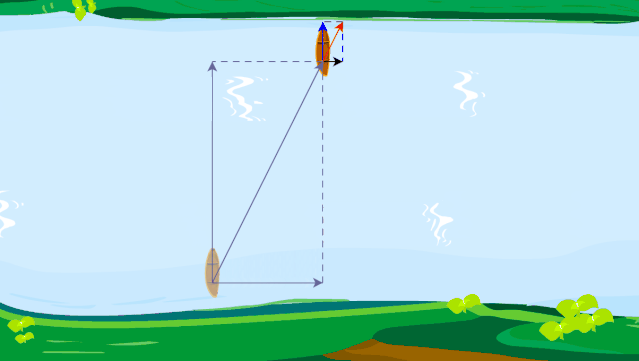
小船如何渡河时间最短
2-2 渡河位移最小问题
(1)问题1：船在静水中的速度为v船，水流的流速为v水，v船>v水．船怎样行驶才能使过河的位移最短呢？最短位移是多少呢？过河时间是多少呢？
分析：船即使不开动自己的动力，也能获得一个水给它的速度v水，即船顺流而下．船还有自己的动力能产生速度v船．
船头朝向不同，船行驶的真实轨迹就会不同，这样船可以行驶出无数条轨迹．很明显其中垂直于河岸的轨迹位移最短．
解决：
①合成法
水给予船的漂流速度大小和方向不变，为了使船的真实轨迹垂直于河岸，就需要通过调整船头方向，使船速与水流速合成一个垂直于河岸的实际过河速度，如下图所示．其中：设船与河岸的夹角为α，则
②分解法
为了抵消水流的影响，船必须有一个逆流而上的速度v船1，且v船1=v水，另外船还必须有一个垂直于河岸过河的速度v船2，它们是v船的两个分速度．所以，船头必须沿斜向上游方向行驶．设船与河岸的夹角为α，则
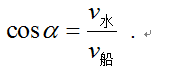
以上两种分析方法殊途同归，得到相同的结论：
虽然这样过河位移最短，但是，时间不是最短的哦！
(2)问题2：船在静水中的速度为v船，水流的流速为v水，v船
分析：船是否能垂直河岸过河呢？因为v船船走不出垂直于河岸的轨迹．
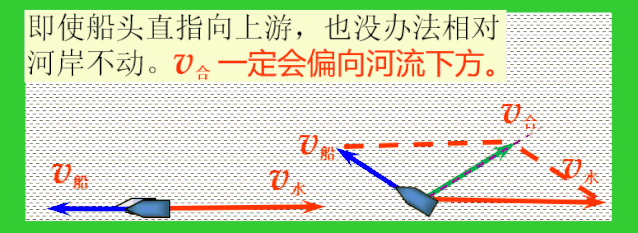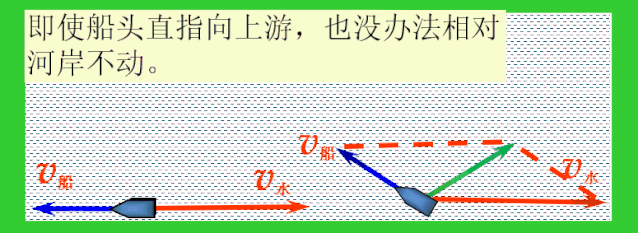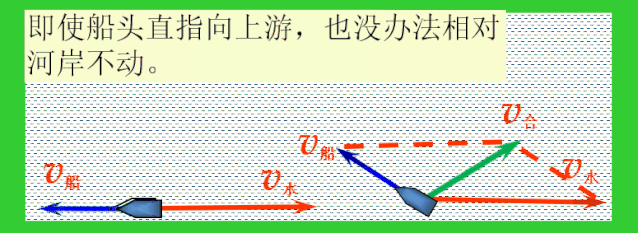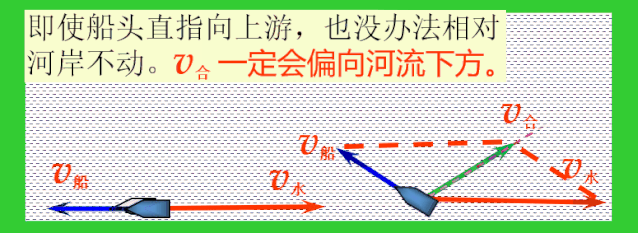
虽然走不出垂直于河岸的轨迹，但是由于船头不同的指向，依然可以走出无数条不同的轨迹，在这些轨迹中跟河岸的夹角最大的轨迹位移最短．
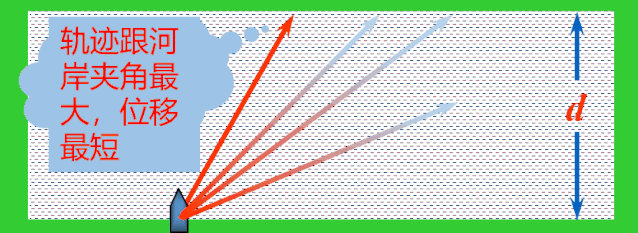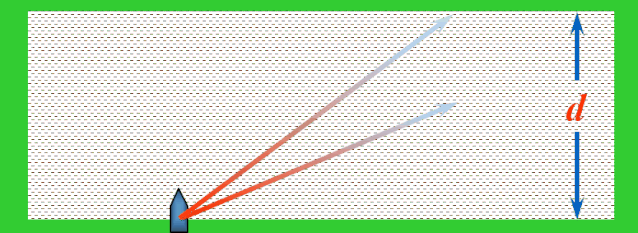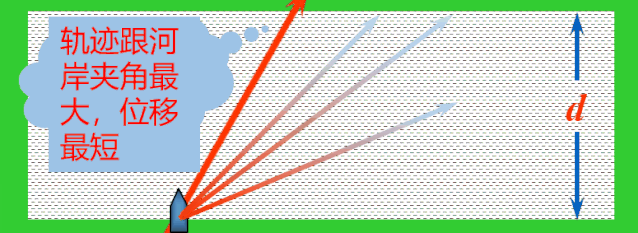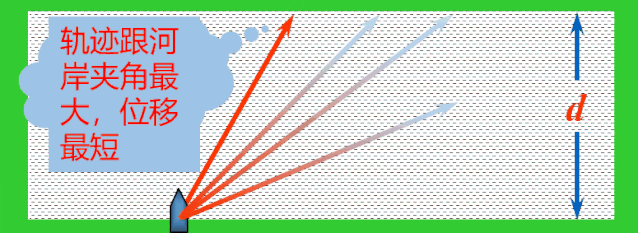
解决：当船头指向与水流方向成θ角时，依据运动合成的平行四边形定则，船的实际运动速度v合表示如图．
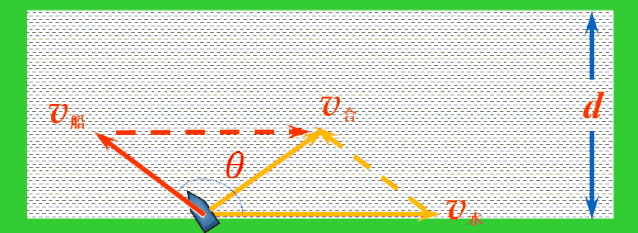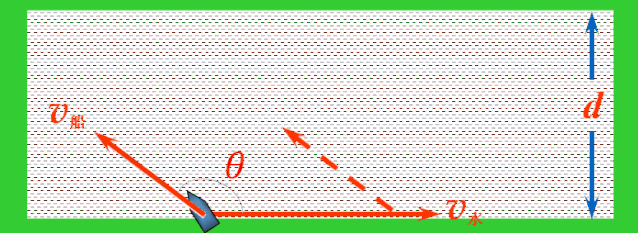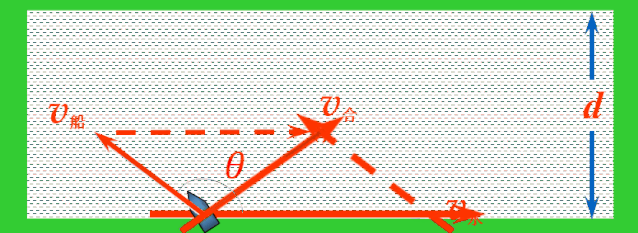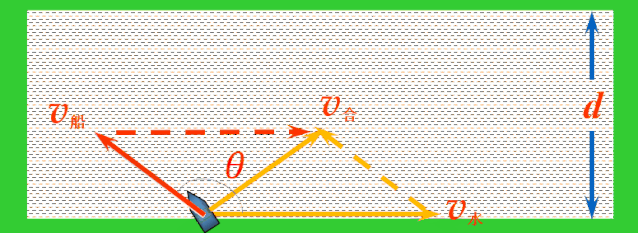
应用矢量三角形法则，平移v船，使v船和v水首尾相接，连接v水的首端和v船的尾端的有向线段就是v合．
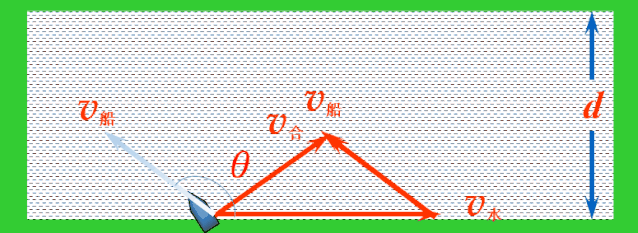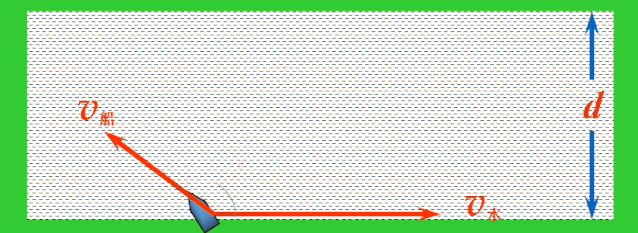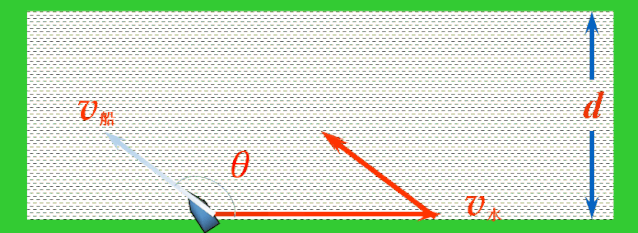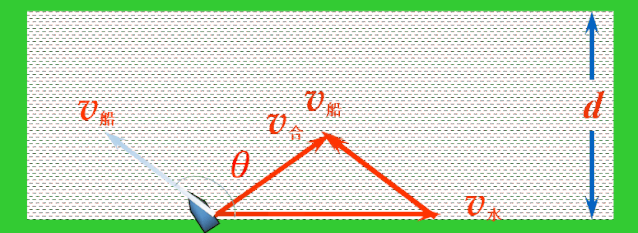
随着船头指向变化，v船绕着v水的尾端形成一个半圆，v水不变，v合的大小与方向均发生变化．当v合与半圆相切时，与河岸的夹角最大，这时船过河的位移最短．
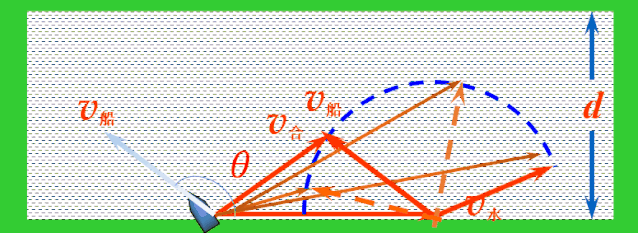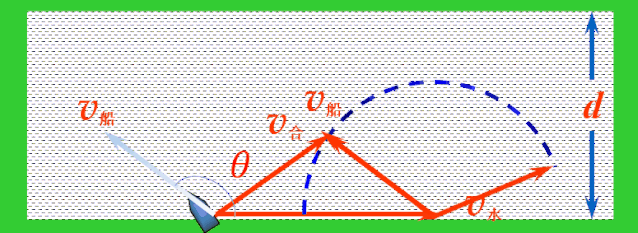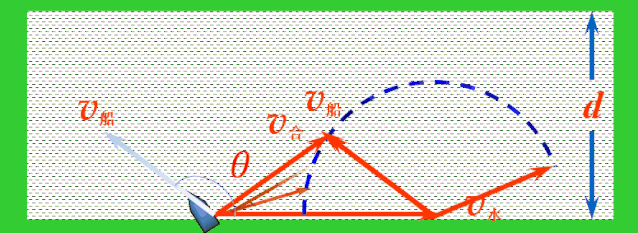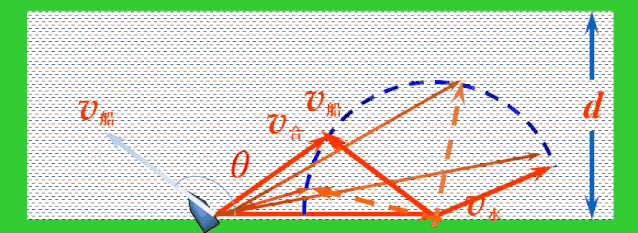
当v合与半圆相切时，v合与v船成直角，设船头跟河岸的夹角为α，则有：
cos α=v船/v水，(α与θ互补)
v合=v水sin α
最短位移xmin＝d/cos α
过河时间t=d/(v船sin α)
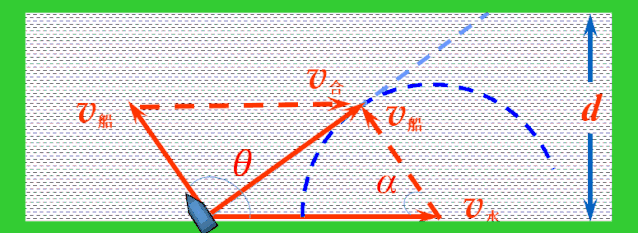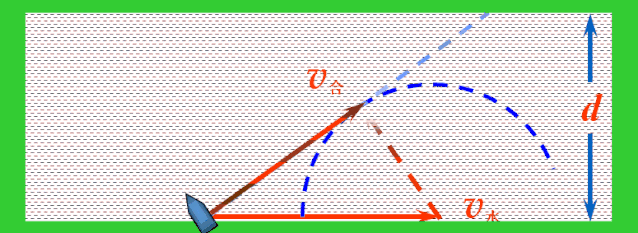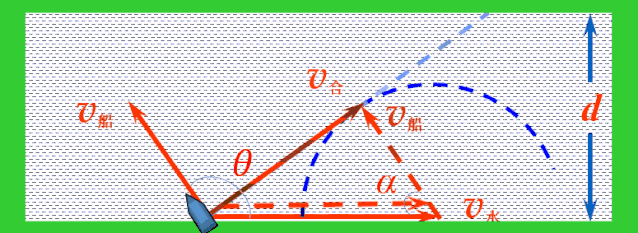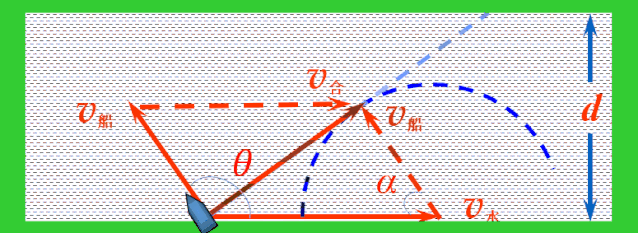
当面对复杂问题没有头绪的时候，聪明的人总是先任选一种情况进行探索，找一下规律，例如刚才我们就是通过研究船头与河水流向成θ角时的情况找到了解决问题的方法．
小船如何渡河距离最短？
示范例题
例题1.(解析题)小船要渡过200m宽的河，水流速度为2 m/s，船在静水中的速度为4 m/s．
(1)若小船的船头始终正对对岸，它将在何时、何处到达对岸？
(2)要使小船到达正对岸，应如何航行？历时多久？
(3)小船渡河的最短时间为多少？
(4)若水流速度为5 m/s，船在静水中的速度为3 m/s，则怎样渡河才能使船驶向下游的距离最小？最小距离为多少？(sin 53°＝0.8，cos 53°＝0.6，结果取整数)
【答案】(1)50s时在正对岸下游100m处靠岸；
(3)50s；
(4)船头与上游河岸的夹角为53°；最小距离为267m；
【解析】(1)小船渡河过程参与了两个分运动，即船随水流的运动和船在静水中的运动．因为分运动之间具有独立性和等时性，故小船渡河时间等于它在垂直河岸方向上的分运动的时间，即
小船沿水流方向的位移
s水＝v水t⊥＝2×50m＝100m
即小船将在正对岸下游100m处．
(2)要使小船到达正对岸，即合速度v应垂直于河岸，如下图所示．
则
(3)考虑一般情况，设船头与上游河岸成任意角α，如下图所示．
小船的渡河时间取决于小船垂直于河岸方向上的分速度
v⊥＝v静水sin α
故小船渡河时间为
当α＝90°，即船头与河岸垂直时，渡河时间最短，最短时间为 tmin＝50s．
(4)因为v′静水
设船头(v′静水)与上游河岸成β角，合速度v′与下游河岸成γ角，可以看出γ角越大，船驶向下游的距离x′越小．以v′水矢量的末端为圆心，以v′静水的大小为半径画圆，当合速度v′与圆相切时，γ角最大．
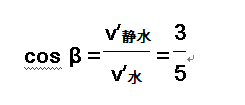
船头与上游河岸的夹角
β＝53°
代入数据解得
x′≈267m．
点拨
小船渡河问题主要考查合运动与分运动的关系，要弄清物理情境．要使小船渡河的时间最短，只要小船在静水中的速度方向垂直河岸即可，但是求渡河的最小位移时，要注意小船在静水中的速度与水流速度的大小关系，选用不同的分析方法．在分析求解具体问题时，要明确小船渡河时其航行的方向为合速度的方向，这是解答此类问题的关键．
0 3 实际运动中的关联速度问题
关联速度问题一般是指物拉绳(或杆)和绳(或杆)拉物问题．高中阶段研究的绳都是不可伸长的，杆都是不可伸长且不可压缩的，即绳或杆的长度不会改变．
1. 速度规律
绳、杆等连接的两个物体在运动过程中，其速度通常是不一样的，但两个物体沿绳或杆方向的速度大小相等，我们称之为关联速度．
2. 解决关联速度问题的一般步骤
第一步：先确定合运动，即物体的实际运动．
第二步：确定合运动的两个实际作用效果，一是沿绳(或杆)方向的平动效果，这个效果改变速度的大小；二是沿垂直于绳(或杆)方向的转动效果，这个效果改变速度的方向．即将实际速度分解为垂直于绳(或杆)和平行于绳(或杆)方向的两个分量．
第三步：按平行四边形定则进行分解，作出运动矢量图．
第四步：根据沿绳(或杆)方向的速度相等列方程求解．
3. 常见的模型
3-1 车拉船模型
问题：车拉船运动，车匀速前进，速度为v，当绳与水平方向成α角时，船速v′是多少？
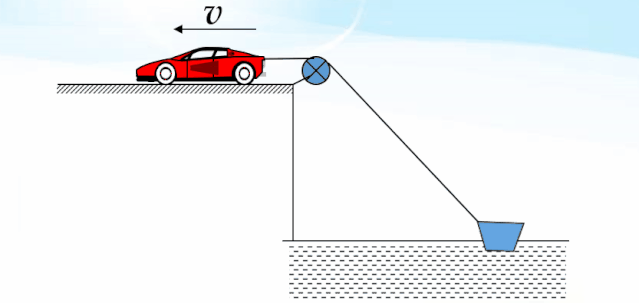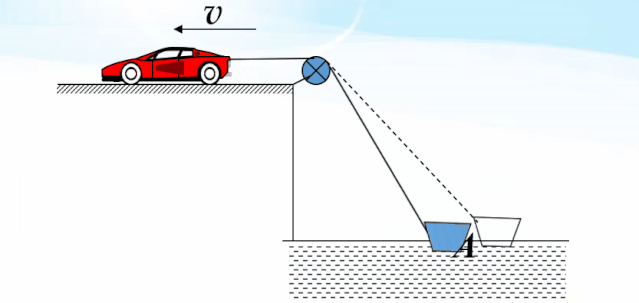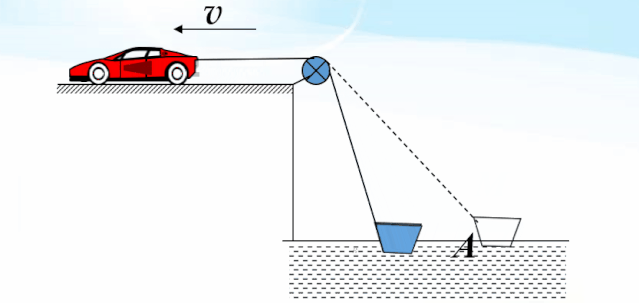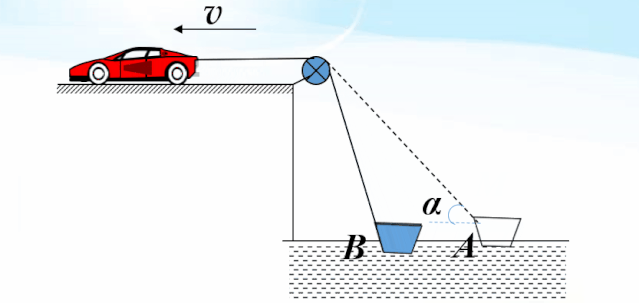
分析：绳与船接触的点M是个特殊的点，此点既在绳上又在船上．在船上，是实际运动(合运动)．在绳上，同时参与两个分运动．
点M从A到B的运动情况比较复杂，为了便于理解和观察，把运动过程等效分解为两个独立的运动过程．一个是绕滑轮做的圆周运动，这个运动不改变绳长，每一时刻的速度方向都垂直于绳的方向．另一个是沿着绳的方向做的直线运动，这个运动是由于车拉动绳向O点收缩引起的．
所以点M的速度每时每刻都可以分解为两个速度．
一个是垂直于绳的方向的v1．
另一个是沿着绳的方向的v2．
则有：
v1=v′sin α
v2=v′cos α
车和船都在同一根绳上，由于绳的长度不会改变，所以车和船的实际速度沿绳方向的分速度大小相同．
解决：车在绳上的分速度等于船在绳上的分速度．即
v=v2
v=v′sin α
所以
v′=v/sin α
绳子的“关联”速度问题
3-2 其他模型
(1)两个物体的绳子末端速度的分解
如下图所示，两个物体的速度都需要分解，其中两个物体的速度沿着绳子方向的分速度是相等的，即vA∥=vB∥．
(2)两个物体的硬杆末端速度的分解
如下图所示，a、b沿杆的方向上各点的速度大小相等．
vacos θ=vbcos α
va：vb=cos α：cos θ
示范例题
例题1.(单选题)固定在竖直平面内的半圆形刚性铁环，半径为R，铁环上穿着小球，铁环圆心O的正上方固定一个小定滑轮．用一条不可伸长的细绳，通过定滑轮以一定速度拉着小球从A点开始沿铁环运动，某时刻小球运动至如下图所示位置，若绳末端的速度为v，则小球此时的速度为( )
【答案】A
【解析】小球的速度方向沿铁环的切线方向，将小球的速度分解为沿绳方向和垂直于绳方向的分量，沿绳方向的速度为v，则v′cos 30°＝v，解得
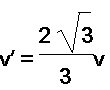选项A正确．
点拨
找准合运动，分解合运动，不能分解分运动．
声明：以上内容摘自包学习APP_动态教辅《高中物理丨必修第二册》，欢迎来包学习和更多小伙伴一起学习更多知识吧。
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
