软渲染器实现过程详解

ProEthan

已于 2022-04-17 11:18:35 修改

阅读量1.1k

点赞数 4

文章标签：矩阵 opengl

于 2022-03-21 17:27:44 首次发布

本文链接：https://blog.csdn.net/weixin_39655480/article/details/108993191

版权

文章目录

前言
一、渲染管线概述
二、渲染管线详解
- 1.顶点输入处理
- 2.顶点着色器
- 3.光栅化
- 4.片段着色器
总结

前言

能够想到自己动手实现一个软渲染器，相信大家都对图形学有所了解，对其中的渲染部分更有一个清晰的认识。你可能用的是OpenGL或者D3D，但是殊途同归，其中的思想是一致的，明白了这个思想，了解渲染管线的流程，自己也可以动手实现一个软渲染器。这个过程是对之前所学知识的一次巩固，并能发现自己在学习过程中遗漏的点，当然，更可贵的是，完成这样一个软渲染器后你会更加坚定自己的发展方向（能够很好的完成它，难道不是真爱？）

开源地址：GitHub/ProEthan/SoftwareRendering

一、渲染管线概述

这是OpenGL渲染管线的一个流程，下面我结合自己实现的软渲染器对这个流程做一个讲解。

1、顶点数据：顶点数据存储在内存中，如何告诉GPU数据在哪？如何让GPU知道传过来的这堆数据是什么？这就涉及到输入处理的问题。关于数据在哪的问题，可以使用C++中的指针来绑定一个内存位置进行标示；关于数据是什么的问题，就可以采用一些描述性的字段啦，OpenGL和D3D11都有各自的实现方式，但是总体还是差不多的，主要是标示这堆顶点数据每个顶点有哪些属性以及每个属性的占用空间和相对开始位置。比如，对于一个三角形：

float triangle[] = {
    -0.5, -0.5, 0.0, 255, 0, 0, 1,
     0.5, -0.5, 0.0, 0, 255, 0, 1,
     0.0,  0.5, 0.0, 0, 0, 255, 1,
};

相信大家能猜到，每行的前3个float是顶点的位置，后四个float是顶点的RGBA值。但是计算机猜不到啊，所以在这个阶段你还需要解释这些数据都是什么。可以使用步长、起始位置等标示。最终可以将他们封装到一个结构体数组中，数组中的每一个结构体元素包含一个顶点的所有属性。当然，你也可以有其他的方式来解释和存储顶点数据。

2、顶点着色器：这是渲染管线的开始位置，经过顶点数据的输入处理阶段后，一段有规律的数据就传到了这里。顶点着色器接收一个顶点的输入。可以做一个循环，遍历结构体数组中的每个顶点。在这个阶段，单独处理每一个顶点数据，主要做顶点的空间变换：

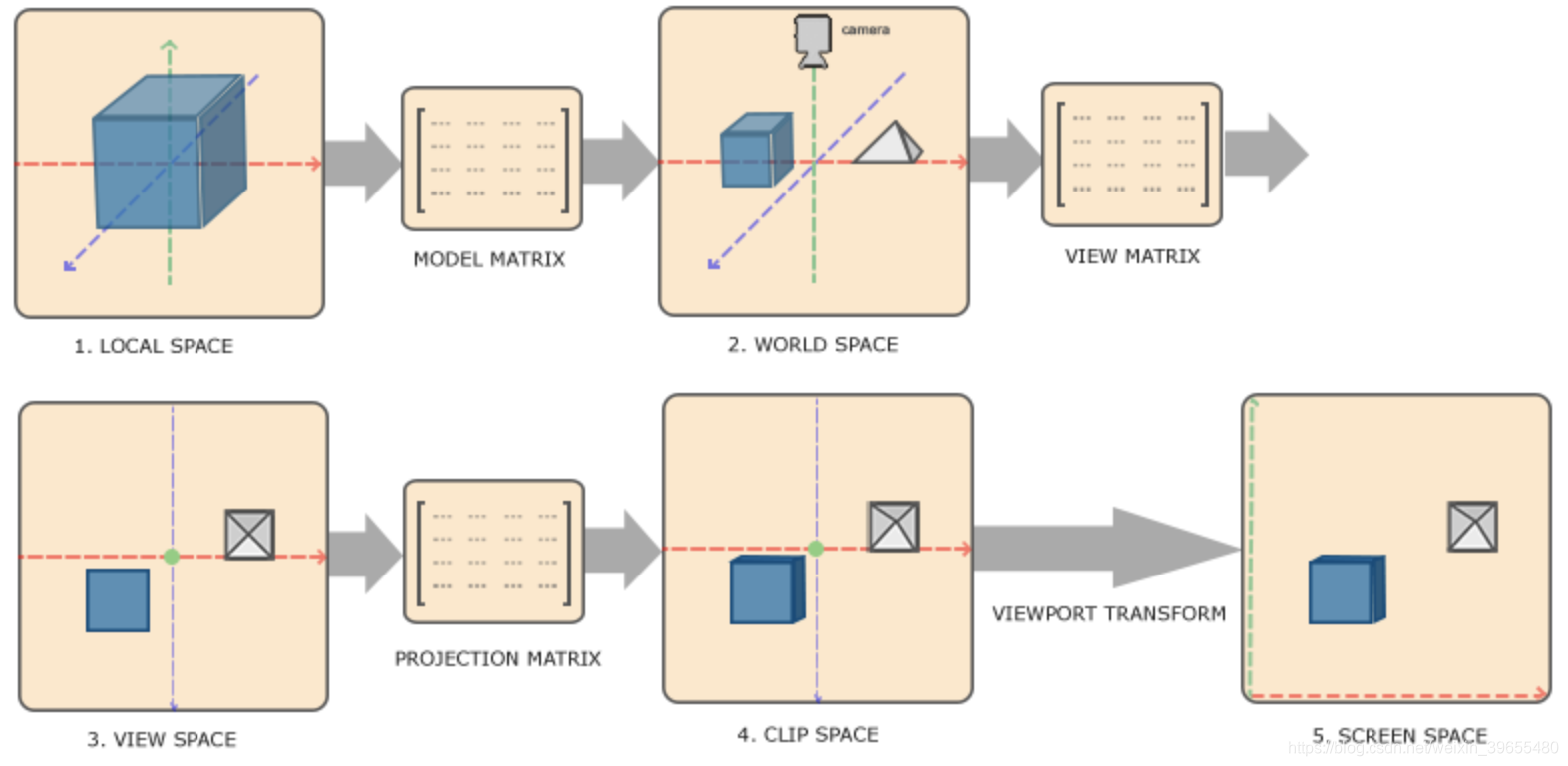
相信学习了一些图形API的你们已经知道怎么做了，其实就是几个矩阵运算，用model矩阵将顶点数据vertex从局部空间变换到世界空间，用view矩阵将从世界空间变换到摄影机空间，再用projection矩阵将其变换到裁剪空间，最后做一个裁剪和透视除法变换到屏幕空间。这其中涉及到几个难点，分别是绕任意轴旋转矩阵的推导、透视投影矩阵的推导之后会详细讲解。

3、图元装配阶段：将空间变换后的一个三角形的三个顶点保存到一个数组中。

4、几何着色器：暂时可以不用处理这个阶段。

5、光栅化阶段：这应该是渲染管线中最复杂的一个阶段，接收三角形三个顶点的输入，输出填充后的三角形内的所有顶点数据，主要是做“插值”。包括顶点插值、纹理坐标插值、法向量插值。

6、片段着色器：光栅化阶段后三角形的顶点数据数量暴增，片段着色器接收一个顶点数据的输入（此时的每个顶点也被称为片段），输出处理完后的一个片段数据。在这个阶段中主要是给每个片段加入颜色、加入光照。最终赋予每个片段以各自的颜色。光照可以参考下Blinn-Phong光照模型，后期拔高的话可以了解下PBR。

二、渲染管线详解

1.顶点输入处理

2.顶点着色器

下面主要讲解几个矩阵的求法：

对于一个顶点坐标 p(x, y, z)，我们如何利用一个矩阵对它进行空间变换呢？想必大家都有所了解，聪明的数学家们引入了齐次坐标这个东西（可以方便位移操作）。也就是对于一个三维空间的顶点再加上一个维度w，既是p(x, y, z, w)。这样做的好处就是我们利用矩阵来实现顶点的空间变换啦。看看具体是怎么做的：

（1）缩放

（2）平移

（3）旋转

首先我们讨论一下二维空间的旋转：

1、二维空间绕原点旋转

对于点 v(x, y)，绕原点 (0, 0) 逆时针旋转 θ 弧度得到 v'(x', y')：

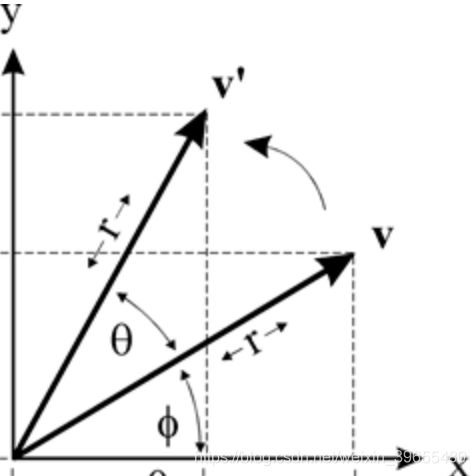
则有：

x = r * cosφ

y = r * sinφ

x' = r * cos(θ + φ) = r * (cosθ * cosφ - sinθ * sinφ) = x * cosθ - y * sinφ

y' = r * sin(θ + φ) = r * (sinθ * cosφ + sinθ * cosφ) = x * sinθ + y * cosφ

则有：

$\begin{bmatrix} x'\\ y' \end{bmatrix}$ = $\begin{bmatrix} cos\theta &-sin\theta \\ sin\theta & cos\theta \end{bmatrix}$ * $\begin{bmatrix} x\\ y \end{bmatrix}$

2、二维空间绕任意点旋转

绕任意点 (p, q) 旋转 θ 弧度，可以拆分成三步：将这个任意点平移到原点、绕原点旋转、逆操作平移回去。既然涉及到位移，那么就要引入齐次坐标w。

首先对平移到原点：

$\begin{bmatrix} 1 &0 &-p \\ 0&1 &-q \\ 0&0 &1 \end{bmatrix}$ * $\begin{bmatrix} x\\ y\\ 1 \end{bmatrix}$

其次绕原点旋转 θ 弧度：

$\begin{bmatrix} cos\theta & -sin\theta & 0\\ sin\theta & cos\theta & 0\\ 0& 0 & 1 \end{bmatrix}$ * $\begin{bmatrix} 1 &0 &-p \\ 0&1 &-q \\ 0&0 &1 \end{bmatrix}$ * $\begin{bmatrix} x\\ y\\ 1 \end{bmatrix}$

最后逆操作平移回去：

$\begin{bmatrix} 1 &0 &p \\ 0&1 &q \\ 0&0 &1 \end{bmatrix}$ * $\begin{bmatrix} cos\theta & -sin\theta & 0\\ sin\theta & cos\theta & 0\\ 0& 0 & 1 \end{bmatrix}$ * $\begin{bmatrix} 1 &0 &-p \\ 0&1 &-q \\ 0&0 &1 \end{bmatrix}$ * $\begin{bmatrix} x\\ y\\ 1 \end{bmatrix}$

根据矩阵的结合律，前三个矩阵先相乘得到绕任意点旋转的矩阵为：

3、三维空间绕坐标轴旋转（以绕z轴为例）

对于点 (x, y, z)，绕 z 轴旋转 θ 弧度得到 (x', y', z, 1)。其实就是固定 z 不变，映射到 xy 坐标系，就转换到二维空间绕原点旋转啦，是不是很简单。矩阵变换如下：

$\begin{bmatrix} cos\theta & -sin\theta & 0\\ sin\theta & cos\theta & 0\\ 0& 0 & 1 \end{bmatrix}$ * $\begin{bmatrix} x\\ y\\ z \end{bmatrix}$

当然，如果引入齐次坐标w，矩阵变换就如下：

$\begin{bmatrix} cos\theta & -sin\theta & 0 &0 \\ sin\theta & cos\theta & 0 &0 \\ 0& 0&1& 0\\ 0& 0 & 0& 1 \end{bmatrix}$ * $\begin{bmatrix} x\\ y\\ z\\ 1 \end{bmatrix}$

同理，可以得到绕 y 轴旋转的变换矩阵：

绕 x 轴旋转的变换矩阵：

4、三维空间绕起始点为原点的任意轴旋转

如果你懂了二维空间绕任意点的思路，其实就很容易想到三维空间绕任意轴旋转方法。

P点(x, y, z, 1)绕向量u(u, v, w)旋转 θ 角，得到点Q，已知P点的坐标和向量u，如何求Q点的坐标。
我们可以把向量u进行一些旋转，让它与x轴重合，之后旋转P到Q就作了一次绕x轴的三维基本旋转，之后我们再执行反向的旋转，将向量u变回到它原来的方向。

其中：

sinα = u / (u^2 + v^2 + w^2)

cosα = $\sqrt{u^2+w^2}$ / (u^2 + v^2 + w^2)

sinβ = w / $\sqrt{u^2+w^2}$

cosβ = u / $\sqrt{u^2+w^2}$

先将向量u绕z轴旋转 α 得到向量u' ，使u落到xz平面上，对应的P点的旋转变换为P'：

$\begin{bmatrix} cos\alpha & -sin\alpha &0 &0 \\ sin\alpha &cos\alpha & 0&0 \\ 0&0 &1 &0 \\0 &0 & 0&1 \end{bmatrix}$ * $\begin{bmatrix} x\\ y\\ z\\ 1 \end{bmatrix}$

再将 u' 绕y轴旋转 β 得到向量 u''，使 u 落到 x 轴上，对应的P'点的旋转变换为P''：

$\begin{bmatrix} cos\beta & 0 & sin\beta &0 \\ 0 & 1 &0 &0 \\ -sin\beta & 0& cos\beta &0 \\ 0& 0 & 0 & 1 \end{bmatrix}$ * $\begin{bmatrix} cos\alpha & -sin\alpha &0 &0 \\ sin\alpha &cos\alpha & 0&0 \\ 0&0 &1 &0 \\0 &0 & 0&1 \end{bmatrix}$ * $\begin{bmatrix} x\\ y\\ z\\ 1 \end{bmatrix}$

然后将 P'' 绕 u‘’ 旋转 θ 得到 Q''，即点绕x轴旋转，对应的旋转变换为：

$\begin{bmatrix} 1 &0 &0 & 0\\ 0& cos\theta & -sin\theta &0 \\ 0& sin\theta &cos\theta & 0\\ 0& 0& 0& 1 \end{bmatrix}$ * $\begin{bmatrix} cos\beta & 0 & sin\beta &0 \\ 0 & 1 &0 &0 \\ -sin\beta & 0& cos\beta &0 \\ 0& 0 & 0 & 1 \end{bmatrix}$ * $\begin{bmatrix} cos\alpha & -sin\alpha &0 &0 \\ sin\alpha &cos\alpha & 0&0 \\ 0&0 &1 &0 \\0 &0 & 0&1 \end{bmatrix}$ * $\begin{bmatrix} x\\ y\\ z\\ 1 \end{bmatrix}$

然后的然后就是，这个前两步的逆操作啦：

逆操作的第一步，将 u'' 绕 y 轴旋转 -β ，对应的 Q''点的旋转变换为Q' ：

$\begin{bmatrix} cos\beta & 0 & -sin\beta &0 \\ 0 & 1 &0 &0 \\ sin\beta & 0& cos\beta &0 \\ 0& 0 & 0 & 1 \end{bmatrix}$ * $\begin{bmatrix} 1 &0 &0 & 0\\ 0& cos\theta & -sin\theta &0 \\ 0& sin\theta &cos\theta & 0\\ 0& 0& 0& 1 \end{bmatrix}$ * $\begin{bmatrix} cos\beta & 0 & sin\beta &0 \\ 0 & 1 &0 &0 \\ -sin\beta & 0& cos\beta &0 \\ 0& 0 & 0 & 1 \end{bmatrix}$ * $\begin{bmatrix} cos\alpha & -sin\alpha &0 &0 \\ sin\alpha &cos\alpha & 0&0 \\ 0&0 &1 &0 \\0 &0 & 0&1 \end{bmatrix}$ * $\begin{bmatrix} x\\ y\\ z\\ 1 \end{bmatrix}$

逆操作的第二步，将 u' 绕 z 轴旋转 -α ，对应的 Q' 点的旋转变换为 Q ：

$\begin{bmatrix} cos\alpha & sin\alpha &0 &0 \\ -sin\alpha &cos\alpha & 0&0 \\ 0&0 &1 &0 \\0 &0 & 0&1 \end{bmatrix}$ * $\begin{bmatrix} cos\beta & 0 & -sin\beta &0 \\ 0 & 1 &0 &0 \\ sin\beta & 0& cos\beta &0 \\ 0& 0 & 0 & 1 \end{bmatrix}$ * $\begin{bmatrix} 1 &0 &0 & 0\\ 0& cos\theta & -sin\theta &0 \\ 0& sin\theta &cos\theta & 0\\ 0& 0& 0& 1 \end{bmatrix}$ * $\begin{bmatrix} cos\beta & 0 & sin\beta &0 \\ 0 & 1 &0 &0 \\ -sin\beta & 0& cos\beta &0 \\ 0& 0 & 0 & 1 \end{bmatrix}$ * $\begin{bmatrix} cos\alpha & -sin\alpha &0 &0 \\ sin\alpha &cos\alpha & 0&0 \\ 0&0 &1 &0 \\0 &0 & 0&1 \end{bmatrix}$ * $\begin{bmatrix} x\\ y\\ z\\ 1 \end{bmatrix}$

至此，我们就完成啦，成功的将P点旋转到了Q点！虽然有点绕，但是思路是不是很简单。

最后将前面的矩阵相乘得到最终的旋转矩阵：

如果向量 u 是经过单位化的，则有 u^2 + v^2 + w^2 = 1，上式则变为（记为M）：

5、三维空间绕起始点任意点的任意轴旋转

哈哈，这一步当然也是如法炮制的啦。

先将这个任意点平移到原点，再绕过原点的任意轴旋转，然后做逆操作平移回来，就得到最终的旋转变换矩阵啦！

假设这个任意点为 D(a, b, c)，方向向量为 u(u, v, w)。由于会用到上面👆的矩阵M，下面👇就直接用M啦。

首先，做平移操作，将D点平移到原点，对应的矩阵变换为：

$\begin{bmatrix} 1 &0 & 0 & -a\\ 0& 1& 0 &-b \\ 0& 0& 1& -c\\ 0& 0& 0 & 1 \end{bmatrix}$ * $\begin{bmatrix} x\\ y\\ z\\ 1 \end{bmatrix}$

接着，绕起始点为原点的任意轴旋转，对应的旋转矩阵为：

M * $\begin{bmatrix} 1 &0 & 0 & -a\\ 0& 1& 0 &-b \\ 0& 0& 1& -c\\ 0& 0& 0 & 1 \end{bmatrix}$ * $\begin{bmatrix} x\\ y\\ z\\ 1 \end{bmatrix}$

然后，就是平移的逆操作啦，对应的旋转矩阵为：

$\begin{bmatrix} 1 &0 & 0 & a\\ 0& 1& 0 &b \\ 0& 0& 1& c\\ 0& 0& 0 & 1 \end{bmatrix}$ * M * $\begin{bmatrix} 1 &0 & 0 & -a\\ 0& 1& 0 &-b \\ 0& 0& 1& -c\\ 0& 0& 0 & 1 \end{bmatrix}$ * $\begin{bmatrix} x\\ y\\ z\\ 1 \end{bmatrix}$

最终就得到绕起始点为任意点的任意轴旋转的变换矩阵啦

思路是不是很简单！

（4）投影变换矩阵

前面的操作将顶点从局部空间转换到世界空间，然后可以加上摄影机（原理其实就是上面的基础空间变换，通过反向平移、缩放、旋转顶点来模拟摄影机），这就到了摄影机空间，然后就是我们接下来要讲的啦——裁剪空间。

裁剪空间需要做两件事：投影和裁剪。

投影：将坐标标准化。有正交投影和透视投影两种。

裁剪：标准化坐标后，裁剪掉（-1，1）^3之外的顶点。

1、正交投影

大体上，我们拆分为三个主要步骤：正则、规范、标准。

首先我们要定义一个可见的空间区域——正交空间，由于是正交投影，那么这个空间区域是一个长方体，分别指定它的近平面、远平面、左平面、右平面、上平面、下平面。规定里面的顶点可见，外面的顶点则裁剪掉。

接着我们做一个标准化。

第一步（平移）：我们首先将顶点坐标平移到以原点为中心点的位置。

第二部（缩放）：缩放至空间为（-1，1）^ 3

对应的矩阵运算为：

这样我们就得到来一个标准化空间。

正交投影的方式比较简单，直接将x，y映射到view，（-1，1）范围外的则裁剪掉；z<-1或者z>1的顶点也裁剪掉。

2、透视投影

透视投影定义的透视空间与我们的真实人眼所见的空间很像——近大远小的现象。所以，它与上面定义的正交空间不同：（左边定义的是透视(可见)空间）

如何判断一个顶点在透视空间内，如何计算它投影到view上的位置（x，y），就是我们接下来要做的。

透视投影比正交投影复杂一点。但是我们在之前的学习中已经掌握了很好的方法——化繁为简。

首先将透视投影转化为正交投影，再利用上面已有的正交投影的方法解决问题。这样的话，问题就变得简单了，如何将透视空间转化为正交空间呢？

就是给定透视空间内一点（x，y，z，w），如何将它转化为正交空间内的（x‘，y’，z'，w‘）

并且，我们最终的目的是找到这样一个矩阵 M 来表示这个转换过程！

我们先记住两大法宝：

1)任何近平面上的点不会改变；任何远平面上点的 z 不会改变。

2)相似三角形原理。

根据相似三角形原理，我们有如下转换：

y' = （n / z）* y

x‘ = （n / z）* x

但是我们还不知道 z‘ 怎么求，于是我们就要做如下求解啦

我们的输入是（x, y, z, 1），我们的输出是（nx / z, ny / z, unknown, 1）。如何求这个unknown的 z' 呢？

首先，我们将向量乘以 z，得到（nx, ny, z', z）

我们用一个矩阵 M 来表示这个过程：（直接亮出矩阵）

即，转换过程如下：

肯定有同学疑问为什么转换矩阵 M 一定是这个呢？可以结合之前学习的矩阵实现缩放来解释。同学自行脑补。

所以接下来就是求这几个（？？？？）都是些啥啦

这时就要用到我们另外一个已知条件了：

1\任何近平面上的点不会改变； 2\任何远平面上点的 z 不会改变。

由条件 1，我们有：

所以我们可以得到（？，？，？，？）为（0，0，A，B）的形式。即

（我们要记住：n^2 和 xy 没有任何关系）

接下来就是如何求A，B 了，我们得到方程

接着，由条件 2 任何远平面上点的 z 不会改变。我们有：

联立这两个方程，求A，B

终于，我们就得到了这样一个矩阵 M 将透视空间坐标转化为正交空间坐标。

再结合之前的正交投影矩阵，我们就能得到最终的透视投影矩阵啦

同学们自己将两个方程相乘一下吧～

终于终于，我们顺利的走完了顶点着色器阶段。

3.光栅化

在光栅化阶段主要就是接收三角形三个顶点的输入，输出填充后的三角形内的所有顶点数据，主要是做“插值”。包括顶点插值、纹理坐标插值、法向量插值。

主要是做循环遍历然后线性插值，整体项目代码请参考 GitHub项目RasterizateShader.h文件。

/*
*	RasterizateShader: 光栅化阶段
*	
*	输入： 一个图元的数据:图元的顶点的Vertex数据 _vertexs
*
*	输出： 一个图元内所有顶点的Vertex数据 _resVertexs
*/


/* 
* 法向量插值：
* v1：顶点1；
* v2：顶点2；
* prop：两顶点所连线段上某点所在相对位置比例；
*/
glm::vec3 NormalCalc(Vertex v1, Vertex v2, float prop) {
	glm::vec3 n1 = v1.GetNormal();
	glm::vec3 n2 = v2.GetNormal();
	glm::vec3 normal = prop * n1 + (1 - prop) * n2;
	return normal;
}

/* 
* 颜色插值：
* leftColor：顶点1的颜色值；
* rightColor：顶点2的颜色值；
* prop：两顶点所连线段上某点所在相对位置比例；
*/
glm::vec4 LinerColorInterpolationCalc(glm::vec4 leftColor, glm::vec4 rightColor, float proportion) {
	glm::vec4 interColor;
	interColor = proportion * leftColor + (1 - proportion) * rightColor;
	return interColor;
}

纹理贴图：

如果是纹理贴图，那么需要先将图片解析成本地数据。使用std::vector<glm::vec4> texture 存放纹理的所有颜色数据。

4.片段着色器

光栅化阶段后三角形的顶点数据数量暴增，片段着色器接收一个顶点数据的输入（此时的每个顶点也被称为片段），输出处理完后的一个片段数据。在这个阶段中主要是给每个片段加入颜色、加入光照。最终赋予每个片段以各自的颜色。光照可以参考下Blinn-Phong光照模型，后期拔高的话可以了解下PBR。

整体代码请参考GitHub项目FragementShader.h。

/*

*    FragementShader: 片段着色器

*    输入：

	一个片段的的颜色值 vertexColor 
	一个片段的法向量 vertexNormal
	一个片段的位置 vertexPosition

*    输出：

	一个片段最终的颜色 FragColor

*/

总结

呜呜~ 顶点着色器解析写完之后就鸽了两年，导致后面光栅化阶段和片段着色器阶段草草了事。所以本篇文章主要还是顶点着色器的数学思想方面，希望在这一点上能给大家带来一点帮助吧。

ProEthan

关注

4
点赞
踩
5

收藏

觉得还不错? 一键收藏
0
评论
软渲染器实现过程详解

文章目录前言一、渲染管线概述二、渲染管线详解 1.顶点输入处理 2.顶点着色器 3.光栅化 4.片段着色器总结前言能够想到自己动手实现一个软渲染器，相信大家都对图形学有所了解，对其中的渲染部分更有一个清晰的认识。你可能用的是OpenGL或者D3D，但是殊途同归，其中的思想是一致的，明白了这个思想，了解渲染管线的流程，自己也可以动手实现一个软渲染器。这个过程是对之前所学知识的一次巩固，并能发现自己在学习过程中遗漏的点，当然，更可贵的是，完成这样一个软渲...
复制链接

扫一扫