盛金公式解一元三次方程_无法“解”出的方程——论一般五次方程没有求根公式...

古典代数学有一个经典的结论，五次（含）以上的方程没有求根公式，这里所谓的求根公式只涉及加、减、乘、除以及开任意次根；这一结论被称为Abel-Ruffini定理。要得到上述结论通常需要借助抽象代数，而本文将介绍一个较为初等的证明。这个证明来源于Vladimir Arnold。

下文中带*号的部分选读。

一、复数

在那个只有整数的年代，为了使这样的方程

有解，我们引入了形如

的无理数。之后，为了让

有解，我们又人为地引入了虚数

，它和其他的数组合在一起形成复数，组成了复数域

。数学家证明了在复数域内讨论一元任意次方程是合理的，不仅每个方程都有解，而且解的个数还是一定的，等于方程的次数。

代数学基本定理 任意的一元

次复系数方程在

内恰好有

个解（部分解可能重合）。

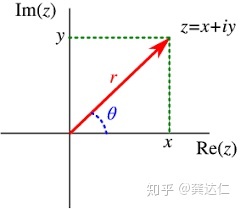
通常情况下，复数

有两种表示方法。一个较为直接的形式是

，其中

和

是实数；

被称为该复数的

实部（Real part），而

被称为是

虚部(Imaginary part)；记

和

。然而，由于欧拉公式

，任何复数也可以写作

，其中

是一个非负数，被称为

模长（Modulus），而弧度

被称为

辐角（Argument）；

和

。两种表示方法可以由下图联系起来（箭头的末端代表这个复数）。

二、复数域中的根式

相信大家都熟悉这个符号，

——给定一个

正实数

，与之相结合可以得到

，它是

的一个

次根。所以，

总可以给出一个正实数的

次根，但是只能给出一个 。根据代数学基本定理，在复数域上任意复数都恰好有

个

次根（计上重数）。所以，现在我们希望把这个符号的作用域扩展到复数域上。

对于任意复数

，我们定义

；

总是一个正实数，所以

可以采用原来的定义，而棘手的部分在于

：以上图为例，我们不改变

，让

加上

，

所代表的仍是同一个复数，因为红色箭头旋转360°后回到了原来的位置。事实上，我们可以在

上增加任意个

并使其仍代表同一个复数，所以

，并且把留在

内那个的辐角

称为

主辐角（Principal argument），记为

，因此

。新的

的作用乍看起来很复杂，但是它有一个优点，它可以给出任意一个复数所有的

次根。

假设我们要找出所有

的三次根。旧的根式符号只能给出一个平凡的三次根，就是它本身。让我们看看推广后的根式符号能带给我们什么：

坐落在复平面的正实轴上，易知它的模长是

，主辐角为

，所以

，

可以取任意整数。

容易发现，随着辐角的增大，

的

个相异的三次根会周期性地依次出现。

新的根式符号尽管可以帮我们找到任意复数的所有

次根，但它有一个致命的缺陷：它不是一个函数；比如把

喂给

，会产生

个对应值，而正常的函数只允许有一个对应值。根据上面的分析，造成这种多值性的原因是对于一个复数的辐角，我们可以有多种不同的选择；比如

，它的辐角可以是

或是

或是任意

，尽管

还是

，但它经过

的作用后却会变成不同的值。我们称这样的映射为一个

多值函数（multi-valued function）。

总而言之，对于一个数

，一旦其辐角被指定为一个唯一值，那么在

作用之下也只会有一个唯一值。

*三、黎曼曲面（Riemann surface）

第二节中我们提到了多值函数，尽管它们不是通常意义上的函数，但是我们希望具体地研究一下它们——最直接的方法就是研究它们的图像。我们首先来看，

；把每个复数喂给它，然后得到相应的值，把它们画在坐标系中。

由于每个复数需要2个参数来确定，要把一个复函数完全地画出来必须要借助四维坐标系。为了方便，垂直轴只用来显示函数值的实部，而水平面则代表了这个函数的定义域，即整个复平面。正如我们所见，这个螺旋形的曲面扭转两次后自交后回到自身。特别地，自交部分在水平面上的投影是实负轴。我们称这个特别的自交部分为分支切割（Branch cut）。

因为任意复数的二次根有两个，所以对每个复数而言，它们的辐角有两类：两类辐角对应不同的二次根。

考虑多值函数

；

对应第一类辐角，

，其中

和

，

。

对应第二类辐角：

；此时

的辐角为

假设

的辐角一开始是其中一类辐角，随着角度增大，角的类别（只有两类）相互交替，这解释了为什么上面的图像会相交自身。

我们称

和

各自为

的

一个分支（Branch）；尽管

本身不是一个函数，但它的分支是。并且，我们可以证明两个分支在实负轴上都不连续，即任意分支从两个方向逼近辐角为

的复数得到的值不同，更确切地说，互为相反数。

我们把上述两个分支画得更立体些。

现在我们发现可以把(a)和(b)在缺口处粘起来，就可以得到这一节开头处的图像。

这个对应于多值函数

的光滑曲面就被称作它对应的

黎曼曲面（Riemann surface），它可以反过来得到对应函数很多有趣的性质。对与很多其他复杂的多值函数，可视化往往比较困难，但是我们可以利用上述过程来大概地估计曲面的形状；比如，我们可以预期高次根式的黎曼曲面在螺旋了多次以后也会自交地回到自身。

四、五次方程的不可解性

首先介绍一类特殊的多项式，对称多项式（Symmetric polynomial）：一个含有

个变量的对称多项式

满足当任意变量被交换，仍得到同一个多项式。

比如

和

是对称多项式；而

则不是，因为交换

和

得到

，与

并不相等。

一个值得注意的事实是：一个一元多次方程的系数可以由含方程根的对称多项式给出。

考虑一个关于

的一元多次方程

。假设其根为

，于是有

，两边展开以及比较系数可得到

可验证等式右侧皆为对称多项式。

现在我们有一个一般形式的一元五次方程

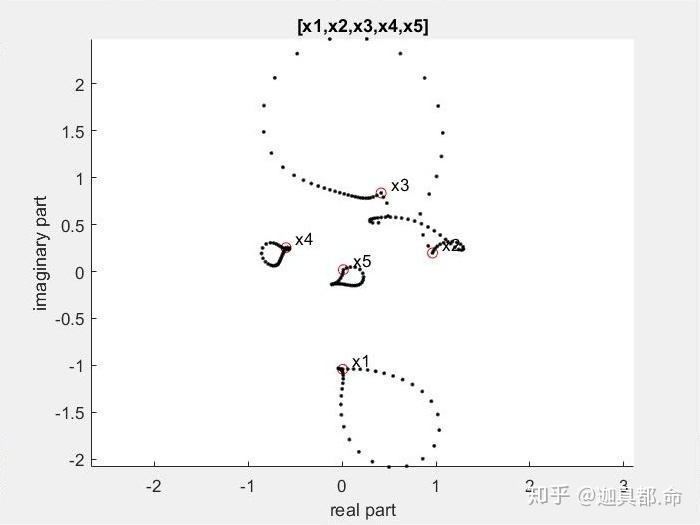
。我们把它的系数和方程的根分别画在两个复平面上（如下两图）。假设现在我们尝试扰动它的五个根，让他们沿着连续的路径交换位置（下图一）：从

变到

——我们称这样的一个操作为

根的连续置换（Permutation）——在这个过程中，对应方程的系数也会相应地偏离它们所在的位置，最终回到起始位置（下图二），因为起点和终点代表的是同一个方程。

假设一个一般的五次方程存在求根公式

，其中

的表达式只涉及方程的

系数以及五种运算——加减乘除和开方。 结合第二节的内容， 只要确定每个系数的辐角，我们就可以利用

唯一地确定一个根；不妨令

。考虑任意一个根的连续置换

，尽管方程的系数本身不会因此改变，但是它们的辐角可能会改变，因而这不能保证在根的连续置换之后，我们仍然有

因为

涉及开方。但是有没有可能存在一个根的连续置换（不是恒等置换

），它不改变所有系数的辐角（因此能让

持续成立），而且还能让

变换到

(假设方程的五个根相异)？这样就可以产生一个矛盾，反证出原来假设的求根公式

不存在。

事实是，存在！

考虑两组关于五个根的连续置换

和

，定义它们的

对易子（Commutator），

。它是一个根的连续置换，重要的是，它不改变方程的系数本身（方程系数是根的对称多项式），

同时也不改变系数的幅角：对于任一个系数，在连续置换

作用后，它的辐角增加了

，在

作用后，又增加了

，最后在

和

的作用后，又分别减少了

和

。

比如，假设

是某一个方程的求根公式，其中

是关于系数的多项式（且系数们都被指定了一个辐角）。基于根的连续置换

，一个一重对易子

不改变

的辐角，即可以保持

，于是乎不会改变

。同理假设另一个一重对易子

也不改变

，那么二重对易子

可以不改变

的辐角，即保持

。同理可得

也保持

。因此，

可以让上述求根公式始终保持在同一个值。在没有任何矛盾的情况下，我们应当确认

，即恒等置换。一般情况下，一个

重根式需要一个

重对易子保持。

五次方程的根的连续置换共有

个——我们令它们组成的集合为

——利用计算机编程可以计算获得所有可能的一重对易子，共有60种——我们令它们组成的集合为

；我们再计算

所有可能的一重对易子，得到的结果还是这60个 。

因此

上所有任意重对易子组成的集合都是

。

假设一个没有重根的五次方程它的求根公式包含

重个根式，我们只要从

中挑

出一个不等于恒等置换的置换——它同时是一个

重对易子——就可以推出矛盾，证明

不存在

。更高次方程的所有根置换的有限重对易子组成的集合至少也包含

中的置换，因此所有高于五次的方程也是不能用根式求解的。*请读者证明一个不含任何根式的表达式不可能是原方程的求根公式。

也许有人会问，既然这种方法能够证明五次方程没有求根公式，那么会不会导出低次方程没有求根公式，这与常识相悖。

考虑一般的二次方程，方程的根

所有可能的置换只有两个

和

。此时的对易子

是恒等置换，所以它不能产生任何矛盾；虽然这个置换不改变所有系数的辐角，同时它也没有让

变换到

。这同时与一般二次方程的求根公式恰好有一个根式相符合。

对于三次方程，对于根的置换

和

，它们对易子

不是恒等置换，因此一般三次方程的求根公式至少会出现两个根式。而对任意四个置换，它们的二重对易子是恒等置换，这与一般三次方程的求根公式含有两重根式相符。

对于四次方程，通过计算可知根的任意八个置换的三重对易子是恒等置换，而存在四个置换它们的二重对易子不是恒等置换，这也与一般四次方程的求根公式有三重根式相符合。

五、结语

如果所有的一元方程都可以被根式求解，那么这意味着它们的根必须具有根式的特征，然而本文证明了，这种对于方程根一厢情愿的期待是不正确的——一些方程的根并不表现得像根式。我们对根式太熟悉，以至于期望用它来解释过分多的事物，如果破除了这种一厢情愿，Abel-Ruffini定理也就不那么令人惊讶了。

参考了Boaz Katz在Youtube上的视频“Short proof of Abel's theorem that 5th degree polynomial equations cannot be solved”总结出此文。最早的证明思路应该归于Vladimir Arnold。

对易子的使用是整个证明中最关键的地方，然而对易子还有其他非常强大的应用，请参见我的另一篇文章：构造属于你自己的魔方公式——解决扭转谜题的系统性方法。