时间复杂度和空间复杂度总结

时间复杂度分析。

一、常用的几种时间复杂度要牢记，即可解决学习和工程项目中的大部分时间复杂度分析。

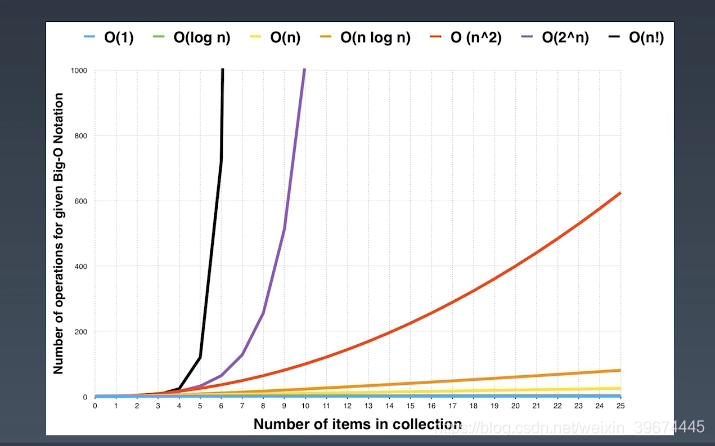
七种常见的时间复杂度：

O(1) :常数级的时间复杂度；

O(N):

O(N^2):

O(2^N)

O(logN)

O(NlogN)

O(N!)

时间复杂度：O(N!) > O(2^N) > O(N^2) > O(NlogN) > O(N) > O(logN) > O(1)

特殊情况分析：递归的时间复杂度分析。

1.采用画递归树的方法来分析递归的时间复杂度。

简单的例子分析：求斐波拉契数列的时间复杂度分析。F(N) = F(N-1) + F(N-2);

2.通过主定理分析时间复杂度。

  任何一个分治和递归都可以通过主定理来分析它的时间复杂度。分治的概念暂且不用理解。

Binary search : 二分查找

Binary tree traversal :二叉树遍历

Optimal sorted matrix search:排好序的二维矩阵进行二分查找。

merge sort:归并排序。

空间复杂度分析

1、数组的长度。

2、递归的深度。