四个角不是直角的四边形_学会构造"一线三等角"模型解题，为中考提分"抄个近路...

"一线三等角"是一个常见的相似模型，指的是有三个等角的顶点在同一条直线上构成的相似图形，这个角可以是直角，也可以是锐角或钝角.通俗地讲，一条直线上有三个相等的角一般就会存在相似的三角形.不同地区对此有不同的称呼，"K形图"，"三垂直"，"弦图"等，以下统称为"一线三等角"模型。

"一线三等角"模型，在三角形全等判定与全等三角形性质、三角形相似判定与相似三角形性质、线段相等、四边形等几何问题中常有应用.我们将从模型介绍与典型例证这两个方面学习"一线三等角"模型。

模型透视

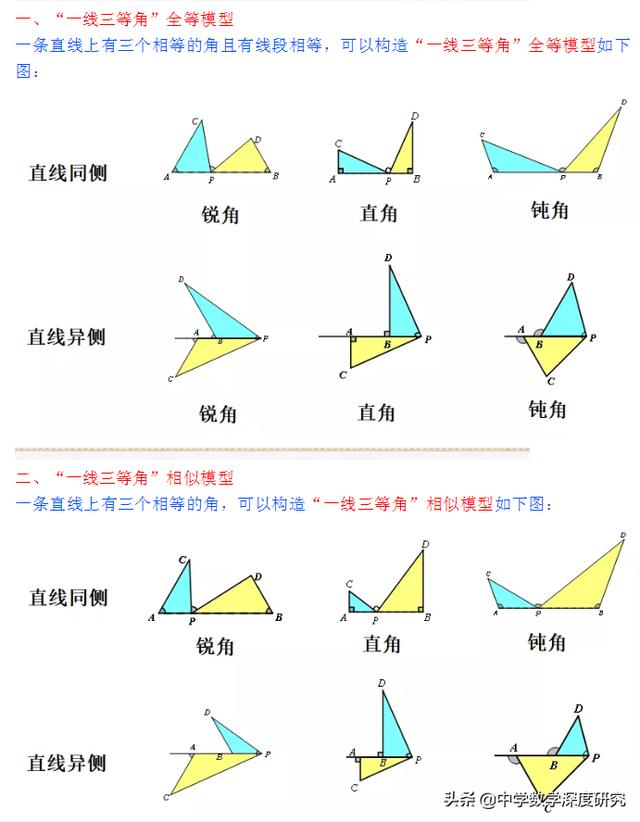
经典考题

1．(2018•遵义中考题)如图，在菱形ABCD中，∠ABC＝120°，将菱形折叠，使点A恰好落在对角线BD上的点G处(不与B、D重合)，折痕为EF，若DG＝2，BG＝6，则BE的长为______．

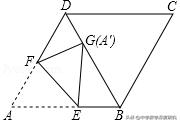
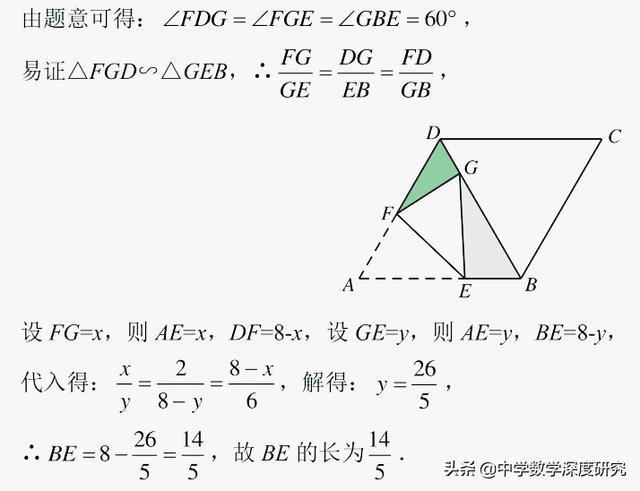
【解析】根据折叠的性质得到一线三等角模型。

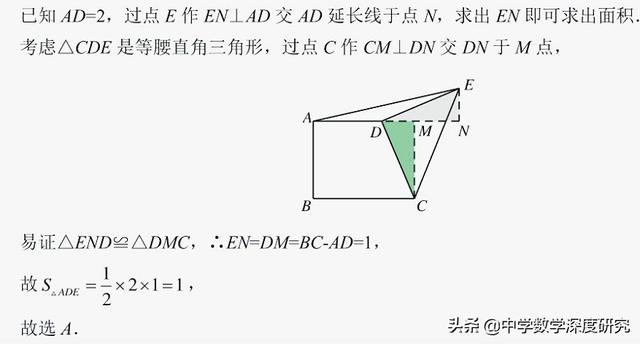
2．如图直角梯形ABCD中，AD∥BC，AB⊥BC，AD＝2，BC＝3，将腰CD以D为中心逆时针旋转90°至ED，连AE、CE，则△ADE的面积是(　　)

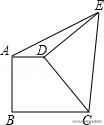
A．1 B．2 C．3 D．不能确定

【解析】如图作辅助线，利用旋转和三角形全等证明△DNE与△DMC全等，再根据全等三角形对应边相等可得ED的长，即△ADE的高，然后得出三角形的面积．

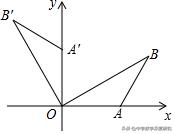
3．(2019•宜昌中考题)如图，平面直角坐标系中，点B在第一象限，点A在x轴的正半轴上，∠AOB＝∠B＝30°，OA＝2，将△AOB绕点O逆时针旋转90°，点B的对应点B'的坐标是(　　)

A．(﹣1，2+√3) B．(﹣√3，3) C．(﹣√3，2+√√3) D．(﹣3，√3)

【解析】如图，作B′N⊥x轴于N, BM⊥x轴于M．构造三垂直模型。

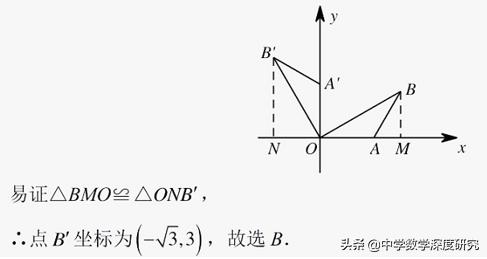
4．(2019•河池中考题)如图，在平面直角坐标系中，A(2，0)，B(0，1)，AC由AB绕点A顺时针旋转90°而得，则AC所在直线的解析式是______．

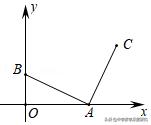
【解析】：∵A(2，0)，B(0，1)∴OA＝2，OB＝1.过点C作CD⊥x轴于点D，

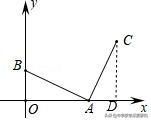
则易知△ACD≌△BAO(AAS).

∴AD＝OB＝1，CD＝OA＝2，∴C(3，2).

设直线AC的解析式为y＝kx+b，将点A，点C坐标代入得，可求得直线AC的解析式为y＝2x﹣4．

变式题.如图3，在平面直角坐标系xOy中，点A的坐标为(﹣1，﹣4)，点B为平面内一点．若△AOB是以OA为斜边的等腰直角三角形，请直接写出点B的坐标．

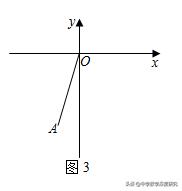
【解答】分两种情况：

①过A作AC⊥y轴于D，过B作BE⊥x轴于E，DA与EB相交于C，如图3所示：则∠C＝90°，

∵点A的坐标为(﹣1，﹣4)，

∴AD＝1，OD＝CE＝4，

∵∠OBO＝90°，

∴∠OBE+∠ABC＝90°，

∵∠ABC+∠BAC＝90°，

∴∠BAC＝∠OBE，

易证△ABC≌△BOE(AAS)，

∴AC＝BE，BC＝OE，

设OE＝x，则BC＝OE＝CD＝x，

∴AC＝BE＝x+1，

∴CE＝BE+BC＝x+1+x＝OD＝4，

∴x＝3/2，x+1＝5/2，

∴点B的坐标(3/2，5/2)；

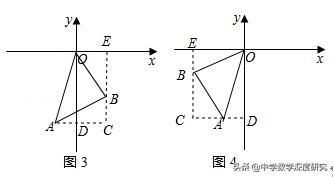
②如图4，同理可得，点B的坐标(﹣5/2，﹣3/2)，

综上所述，点B的坐标为(3/2，5/2)或(﹣5/2，﹣3/2)．

5．(2019•十堰中考题)如图，正方形ABCD和Rt△AEF，AB＝5，AE＝AF＝4，连接BF，DE．若△AEF绕点A旋转，当∠ABF最大时，S△ADE＝______．

【解析】分析知△AEF绕点A旋转时，点F在以A为圆心，4为半径的圆上，当BF为此圆的切线时，∠ABF最大.

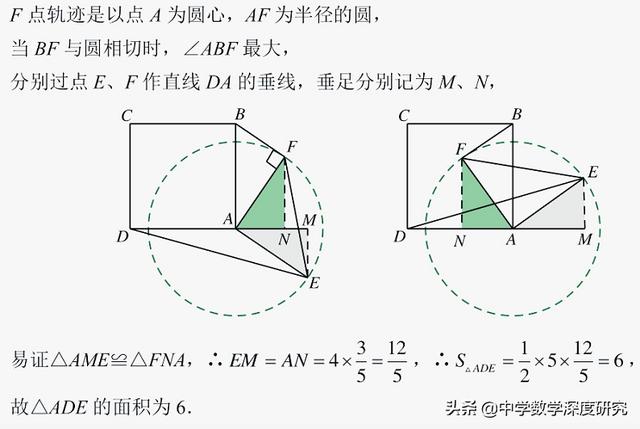
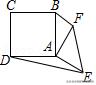
6．(2019•无锡)如图，在△ABC中，AB＝AC＝5，BC＝4√5，D为边AB上一动点(B点除外)，以CD为一边作正方形CDEF，连接BE，则△BDE面积的最大值为______．

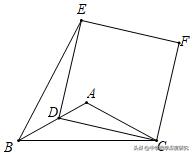
【解析】本题考查了正方形，熟练运用正方形的性质与全等三角形的判定与性质是解题的关键．

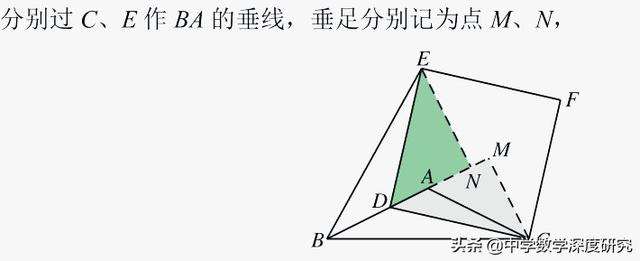
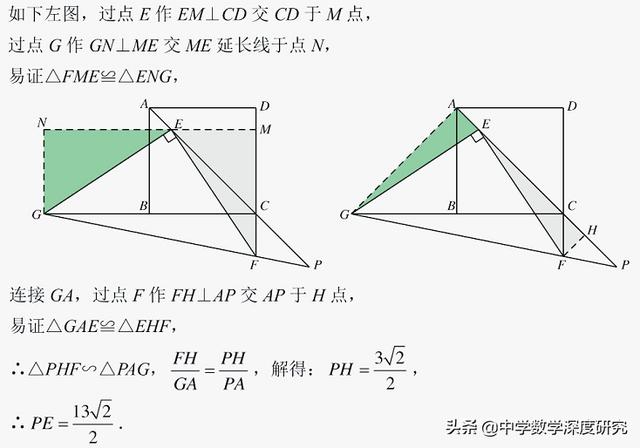
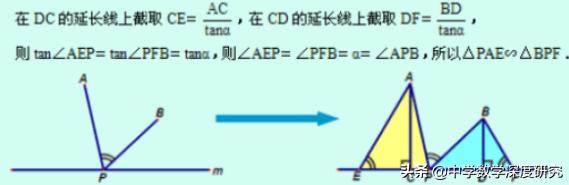
7．(2019•沈阳中考题)如图，正方形ABCD的对角线AC上有一点E，且CE＝4AE，点F在DC的延长线上，连接EF，过点E作EG⊥EF，交CB的延长线于点G，连接GF并延长，交AC的延长线于点P，若AB＝5，CF＝2，则线段EP的长是_______．

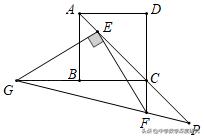
【解析】本题考查正方形的性质，相似三角形的判定和性质，解直角三角形等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，属于中考填空题中的压轴题．

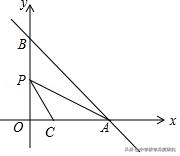
8．(2017•丽水中考题)如图，在平面直角坐标系xOy中，直线y＝﹣x+m分别交x轴，y轴于A，B两点，已知点C(2，0)．

(1)当直线AB经过点C时，点O到直线AB的距离是_______；

(2)设点P为线段OB的中点，连结PA，PC，若∠CPA＝∠ABO，则m的值是_______．

【解析】：(1)当直线AB经过点C时，点A与点C重合，

当x＝2时，y＝﹣2+m＝0，即m＝2，

所以直线AB的解析式为y＝﹣x+2，则B(0，2)．

∴OB＝OA＝2，AB＝2√2．

设点O到直线AB的距离为d，

由S△OAB＝1/2OA2＝1/2AB•d，得4＝2√2d，则d＝√2．

故答案是：√2．

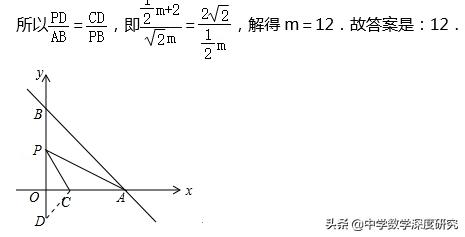
(2)典型的"一线三等角"，构造相似三角形△PCD∽△APB，对m的取值分析进行讨论，在m＜0时，点A在x轴的负半轴，而此时，∠APC＞∠OBA＝45°，不合题意；故m＞0．由相似比求得边的相应关系．

作OD＝OC＝2，连接CD．则∠PDC＝45°，如图，

由y＝﹣x+m可得A(m，0)，B(0，m)．所以OA＝OB，

则∠OBA＝∠OAB＝45°．

当m＜0时，∠APC＞∠OBA＝45°，

所以，此时∠CPA＞45°，故不合题意．所以m＞0．

因为∠CPA＝∠ABO＝45°，

所以∠BPA+∠OPC＝∠BAP+∠BPA＝135°，

即∠OPC＝∠BAP，则△PCD∽△APB，

9．这是一道我们曾经探究过的问题：如图1．等腰直角三角形ABC中，∠ACB＝90°，CB＝CA．直线ED经过点C，过A作AD⊥ED于点D，过B作BE⊥ED于点E．易证得△BEC≌△CDA．(无需证明)，我们将这个模型称为"一线三等角"或者叫"K形图"．接下来，我们就利用这个模型来解决一些问题：

【模型应用】

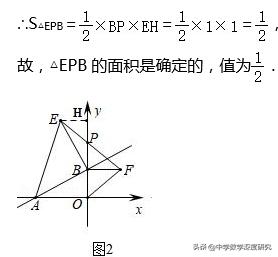
(1)直线AB：y＝1/2x+1与x轴负半轴、y轴正半轴分别交于A、B两点．分别以OB、AB为边，点B为直角顶点在第一、二象限内作等腰直角△OBF和等腰直角△ABE，连EF交y轴于P点，如图2，△EPB的面积是否确定？若确定，请求出具体的值；若不确定，请说明理由．

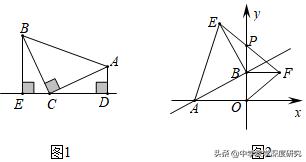
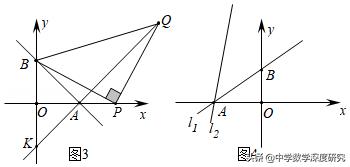
(2)如图3，直线AB：y＝﹣x﹣c分别与x、y轴交于A(3，0)、B两点，P为A点右侧x轴上的一动点，以P为直角顶点，BP为腰在第一象限内作等腰直角△BPQ，连接QA并延长交y轴于点K，当P点运动时，求经过K点且平行于直线AB的直线的函数表达式．

【拓展延伸】

(3)已知直线l1：y＝3/4x+3与坐标轴交于点A、B．将直线l1绕点A逆时针旋转45°至直线l2．如图4，直线l2在x轴上方的图象上是否存在一点Q，使得△QAB的面积与△OAB的面积相等？若存在，求出Q的坐标；不存在，说明理由．

【解析】：(1)直线AB：y＝1/2x+1与x轴负半轴、y轴正半轴分别交于A、B两点．∴A(﹣2，0)，B(0，1)，

过E点作EH⊥y轴，由"K形图"可得△ABO≌△BEH，

∴BH＝OA＝2，HE＝OB＝1，

∵△OBF是等腰直角三角形，

∴OB＝OF＝1，

∴易证△EHP≌△FBP(AAS)

∴PH＝PB＝1，

(2)由直线AB：y＝﹣x﹣c分别与x、y轴交于A(3，0)、B两点，可得c＝3，OB＝3，过Q点作QH⊥x轴，设点P(x，0)，由"K形图"，可得△OBP≌△HPQ；

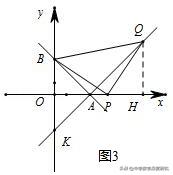
∴OP＝HQ＝x，PH＝OB＝3，

∴HA＝3+(x﹣3)＝x，即HA＝HQ

∴OK＝3，即K(0，3)

∴过K点且平行于直线AB的直线的函数表达式为y＝﹣x﹣3．

(3)过B点作BE⊥AB交l2于C，过C点作CH⊥y轴，

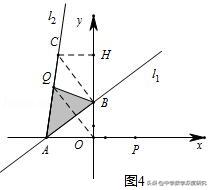
直线l1：y＝3/4x+3与坐标轴交于点A(﹣4，0)、B(0，3)．

由"K形图"，得△AOB≌△BHC，

∴BH＝OA＝4，CH＝OB＝3，

∴C的坐标为(﹣3，7)

故过AC两点的直线l2的解析式为：y＝7x+28，

设Q点坐标为(﹣n，﹣7n+28)，

反思总结

关于"一线三等角"模型的几点说明

"一线三等角"在以正方形、矩形、等腰三角形、等腰梯形为背景的体现很明显，希望可以通过这一题组加以理解，学会灵活运用，解决问题。面对一个个数学问题,若能寻找并建立起它的基本模型,寻找出本质，复杂图形只是在原有简单图形上"添砖加瓦"，层层递进。需要我们把握住这个问题的本质所在,深层挖掘题目所涉及基本思想。

1、"一线三等角"是几何问题中的常见模型，它主要用于导角转换、线段转换与构造全等三角形与相似三角形.

2、导角转换主要基于三角形内角和为180度或平角，利用等式性质实现角度转换.学生在平时解题过程中，要善于总结归纳"一线三等角"基本图形，多关注"一线三等角"模型的提炼、变式与运用.

3、"一线三等角"模型应用的三种情况：(1)图形中已经存在"一线三等角"，直接应用模型解题；(2)图形中存在"一线二等角"，补上"一等角"构造模型解题；(3)图形中只有直线上一个角，补上"二等角"构造模型解题.最后一种情况出现比较多，尤其是压轴题中，经常会有一个特殊角或已知该角的三角函数值时，我经常构造"一线三等角"模型来解题.

4、构造"一线三等角"的步骤：找角、定线、构相似.在直角坐标系中，也可以在x轴或y轴(也可以是平行于x轴或y轴的直线)上构造"一线三等角"模型去求解线段与角度问题.在直角坐标系中，要讲究"线"的特殊性.如下图，线上有一特殊角45度，就考虑构造同侧型"一线三等角".当然只加这两条线通常是不够的，为了利用这个特殊角导线段的关系，过C、D两点作直线l的垂线是必不可少的.两条垂线通常情况下是为了"量化"的需要.如控制AM=CM，BN=DN，可得∠2=∠3=∠1=45°.

一般情况下，如下图，若∠APB=，构造"一线三等角"相似模型如下图所示：