本章首先介绍了什么是学习规则,然后由感知机的结构介绍了感知机的学习规则,并对单神经元感知机的学习规则的收敛性给出了证明,最后讨论了感知机的有点及其局限性。
第四章 感知机学习规则
学习规则
学习规则是指修改网络权值和偏置值的方法和过程,也称为训练算法。学习规则是为了训练网络来完成某些任务。学习规则可以归纳为三大类:有监督学习、无监督学习和增强(评分)学习。
在有监督学习中,学习规则需要一个能够代表网络正确行为的样本集(训练集):
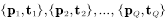
其中
增强学习与有监督学习大体相似,但增强学习不会为每个输入给出相应的目标输出,而仅仅给出一个评分,该评分用来衡量网络在一个序列输入后的性能。增强学习最适合用于控制系统中。
在无监督学习中,网络没有目标输出,其权值和偏置值仅仅依据网络的输入来调节。大多数这类算法用来进行聚类,它们学习把输入数据归到有限的类别中,在向量量化的应用中效果尤其显著。
感知机结构
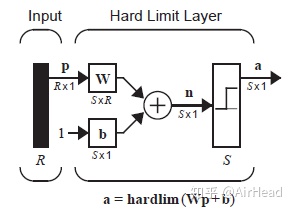
上图是使用hardlim函数作为传输函数的感知机网络,该网络的输出为:
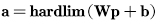
为了可以便捷的使用网络输出中的每一个元素,我们进行以下定义:
首先,网络权值矩阵为:

定义一个由W的第i行构成的列向量:

这样可将权值矩阵划分为:

由此,网络输出向量中的第i个元素可写作:
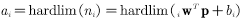
Hardlim传输函数的定义为:
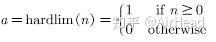
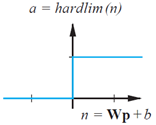
所以,若权值矩阵的第i行和输入向量的内积 大于等于- ,输出 为1,否则输出 为0。也就是说网络中的每个神经元把输入空间划分成了两个区域。
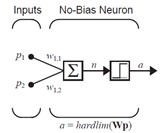
1. 单神经元感知机
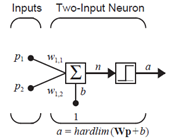
上图为两输入的单神经元感知机,其网络输出可计算为:

其决策边界为:
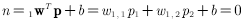
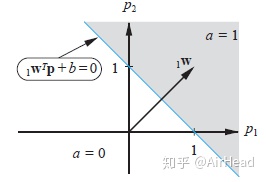
每当给定 时,都能确定平面(输入本身是一个二维空间)中的一条直线,在直线一侧网络输出位0,另一侧输出为1。这条直线与p1 p2轴的交点截距可求得为:
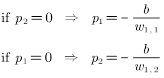
当取
可以通过随意测试一个点的方法,找出决策边界输出为1的那一侧,例如,代入
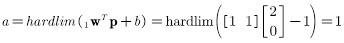
所以决策边界的阴影一侧网络输出为1,另一侧输出位0。
也可以通过作图法找出决策边界。在第三章提到决策边界总是垂直于
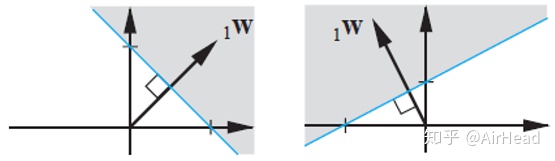
这里给出解释:由于决策边界定义为
其中边界点输入向量在权值向量上相同的投影
2. 多神经元感知机
由单神经元感知机推广,多神经元感知机每一个神经元都有一个决策边界,第i个神经元的决策边界定义为:
由于单神经元感知机输出只能为0或1,所以只能将输入向量分为两类。而多神经元感知机则可以将输入分为许多类,每一类都有不同的输出向量表示。由于输出向量的每一个元素的取值只有0或1,所以一共有
感知机的学习规则
这里感知机的学习规则是有监督学习,而有监督训练的学习规则是从一组能够反映网络行为的样本集中获得的:
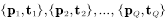
1. 测试问题
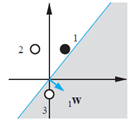
有输入/目标对为:
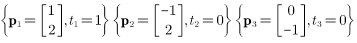
将它们画在二维(两输入)坐标空间输入中,目标输出为0的两个输入向量用○表示,目标输出为1的两个输入向量用●表示。感知机学习的目的就是要解决测试问题,即确定一个决策边界,将○和●区分开。
本问题中网络需要有两个输入一个输出,为了简化学习规则的设计,首先假设网络中没有偏置值,如下图,这样网络只需调整权值参数即可。
去掉了偏置之后,神经网络的决策边界必定穿过坐标轴的原点。为保证简化后的网络依然能解决上述测试问题,从下图可以看出,这样的决策边界有无穷多个。每一个决策边界对应的权值向量与决策边界正交。我们希望学习规则能够找到指向这些方向的一个权值向量。
2. 学习规则的构建
开始训练时,需要给网络的参数赋予初始值。对于两输出/单输出的无偏置网络,所以仅需对两个权值进行初始化:
现在将向量输入网络,首先是
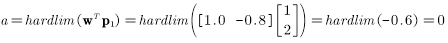
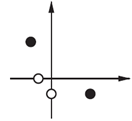
网络没有返回正确的目标值
一种调整方法是直接令
另一种调整方法是将
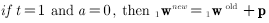
在测试问题中应用这个规则,将会得到新的
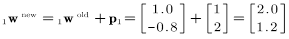
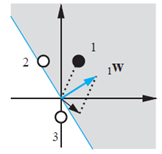
继续考虑下一个向量
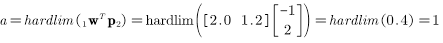
网络没有返回正确的目标值
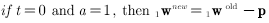
在测试问题中应用这个规则,将会得到新的
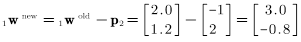
继续考虑下一个向量
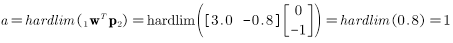
网络没有返回正确的目标值 ,与上一步的操作相同,可以有以下过程:
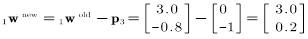
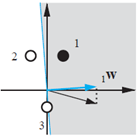
由上图可知,感知机已经可以对上述三个输入向量进行正确的分类,将上述三个输入向量中的任意一个输入神经元感知机将作出正确分类。这就得到了第三条规则:如果感知机能够正确的分类,则不用修改权值向量。
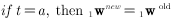
综上所述,考虑到实际输出值和目标值所有可能的组合,有下面三条规则:
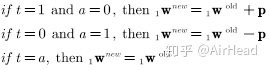
3. 统一的学习规则
定义新变量,即感知机的误差e,e=t-a,将上面的三个规则重写为一个规则,则有:
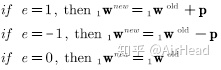
上面三个规则统一形式进一步可以写为:
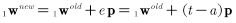
如果把偏置看做一个输入总是1的权值,则可以将上述规则扩展到对偏置的训练过程:
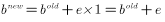
4. 多神经元感知机的训练
由上面单神经元感知机的学习规则,可以按照以下方法推广到多神经元感知机:
权值矩阵第i行的更新方法为:
偏置向量的第i个元素的更新方法为:
感知机的学习规则用矩阵可以表示为:
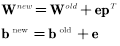
为了验证以上的学习规则,再次考虑第三章开头描述的水果分类问题(唯一不同的地方是用0替换-1),其输入/输出标准向量为:
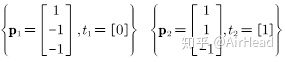
首先,将权值和偏置值初始化为较小的随机数,假设这里的初始矩阵和偏置分别为:
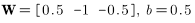
第一次迭代,将
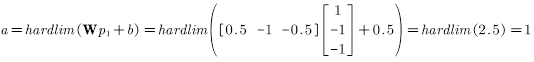
此时的误差:
根据误差更新权值和偏置值:
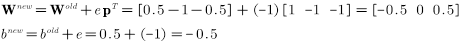
第二次迭代,将
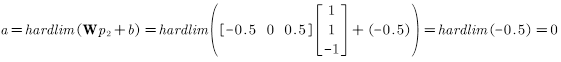
此时的误差:
根据误差更新权值和偏置值:
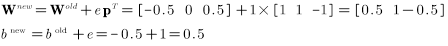
第三次迭代,再次将
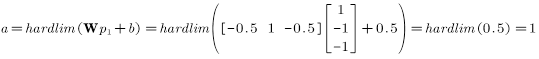
此时的误差:
根据误差更新权值和偏置值:
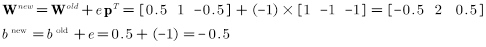
继续迭代下去,最后两个向量都会被正确分类,虽然最后得到的边界可能不唯一,但是都能实现分类的目的。
收敛性证明
感知机的学习规则简单,但却十分有效,下面针对单神经元感知机给出该规则总能收敛到正确分类的权值(若存在)上的证明。
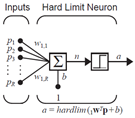
该感知机的输出为:
网络的测试集为:
需要注意的是,证明是在以下三条假设下建立的:
- 问题的存在;
- 仅在输入向量被误分时才改变权值;
- 输入向量模长的上界存在
1. 数学符号
引入以下数学符号,以便描述证明过程。
权值矩阵和偏置值的组合为向量x:
在输入向量中也增加一个常量1,对应于偏置的输入:
则神经元的净输入表示为:
单神经元感知机的学习规则可写作:
权值不变的迭代对收敛性没有影响,如果只考虑权值发生变化的那些迭代,学习规则为:
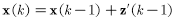
上式中
假设存在对所有Q个输入向量进行正确分类的权值向量,并将这一解记为x*。对该权值向量,假设:
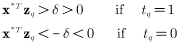
2. 证明
找出算法每一阶段权值向量长度的上界和下界。
先求下界:
取
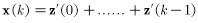
迭代k次后,权值向量和最终权值向量x*之间的乘积为:
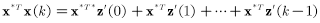
由之前的假设有:
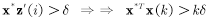
又由Cauchy-Schwartz不等式可得:
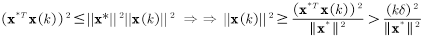
所以由以上两式得到迭代k次后权值向量模长平方的下界为:
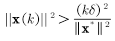
再求上界:
k次改变权值向量后得到的权值向量模长的平方为:
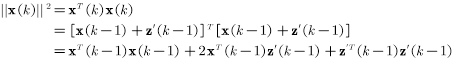
其中,因为权值向量只有在前一输入向量被误分时才会更新,所以有:
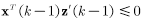
所以:
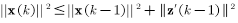
对
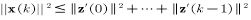
令
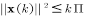
分析上界和下界:
由上面求得的上界和下界,有:
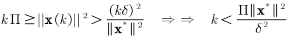
因为k有上界,所以权值的改变次数是有限的。并且k的上界与δ的平方成反比关系。δ刻画了输入模式与决策边界的解的靠近程度,这意味着输入向量越难以分开(越靠近决策边界),越需要更多的迭代次数才能使算法收敛。
3. 局限性
上面证明了只要问题的解存在,那么感知机学习规则就一定能够在有限步数内收敛到问题的一个解上。所以说感知机只能解决解存在的问题,那么什么时候解是存在的,什么时候解又是不存在的。
已经知道,单神经元感知机可将输入空间划分为两个区域,两区域的决策边界可定义为:
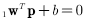
上式定义的决策边界是一个线性边界,也称为超平面(超平面是n维欧氏空间中余维度等于一的线性子空间,也就是必须是(n-1)维度),所以说只要输入向量能被线性边界分开,感知机就可以对这种问题进行分类,这种问题就是解存在的问题。
异或门就是一个典型的线性不可分的例子,其目标输入/输出对是:
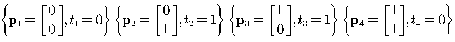
异或门可以由下图表示:
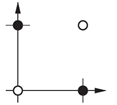
同样线性不可分的问题还有下面两个图形,无法找到一条直线将目标为1和目标为0的向量区分开来:
第11章会讲到求解任意分类问题的多层感知机,以及能用于训练多层感知机的反向传播算法。
例题:考虑具有四类输入向量的分类问题,四个类别如下:
设计一种感知神经网络求解此问题。
解:
使用matlab迭代,程序如下:
clear all
close all
clc
% 定义测试集,P为输入,T为目标输出
P = [1 1 2 2 -1 -2 -1 -2
1 2 -1 0 2 1 -1 -2];
T = [0 0 0 0 1 1 1 1
0 0 1 1 0 0 1 1];
% 根据目标输出维数定义神经元个数
num_neural = size(T,1);
% 根据神经元个数与输入维数定义权值矩阵,并随机初始化
W = rand(size(T, 1), size(P, 1));
% W = [1 0; 0 1];
% b = [1; 1];
% 根据神经元数定义偏置向量,并随机初始化
b = rand(size(T, 1), 1);
while 1
N = 0; % 计算正确次数累计
for i = 1:size(P, 2)
p = P(:, i);
t = T(:, i);
[W, b, e] = update(W, b, p, t);
if norm(e) == 0
N = N + 1;
end
end
if N == size(P, 2)
break;
end
end
% 定义hardlim函数
function a = hardlim(n)
a = n >= 0;
end
% 定义学习函数
function [W, b, e] = update(W, b, p, t)
% 计算净输入
n = W * p + b;
% 计算实际输出
a = hardlim(n);
% 计算误差
e = t - a;
% 学习规则
W = W + e * p';
b = b + e;
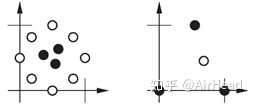
end每运行一次以上程序会得到不同的结果,但均可以把四个类别分开,下图为运行10次所得到的10个不同结果。





















 1万+
1万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








