画数轴的步骤_初中数学——数轴定义、意义及应用

数学是研究数和形的学科。表面看来，数和形好似两码事，其实，在数学里数和形是密切联系的。我们常常用代数的方法来处理几何图形问题，反过来，也借助于几何图形来理解代数概念，寻找解题思路。这种数与形之间的相互应用，是一种重要的数学思想。

运用数形结合思想的关键是建立数与形之间的联系,那么,如何建立数与形之间的联系呢？现在有了一个很好的工具——数轴。

那么,什么叫做数轴？怎样画一条正确的数轴？如何用数轴上的点表示数的呢？这就是我们今天要学习的内容。

一、数轴的定义

1.在古代，部落酋长上任时先在绳上打了个红绳结表示财物往来从0开始，如捕获一只羊在红绳结右边顺次打一个结，每向其他部落借一只羊就在红绳结左边顺次打一个结，你能解读如图所示A、B两处绳结的含义吗？

A的意义是捕获了两只羊，B的意义是向其他部落借了3只羊。

2.你会读温度计吗？

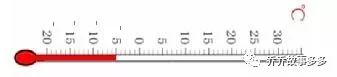
(1)温度计刻度的正负是怎样规定的？以什么为基准？基准刻度线表示多少摄氏度？

以零摄氏度为基准刻度线，超过零摄氏度为正，低于零摄氏度为负。

(2)每摄氏度两条刻度线之间的距离有什么特点？

每两条刻度线之间的距离是相等的。

3.数轴的定义

在数学上，数轴就是规定了原点、正方向和单位长度的直线叫做数轴。

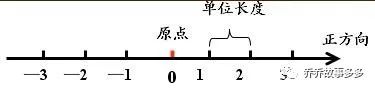
4.注意事项：

(1)数轴是一条特殊的直线；

(2)通常规定直线上从原点向右(或上)为正方向，从原点向左(或下)为负方向；

(3)选取适当的长度为单位长度。

二、怎样画数轴

画数轴的步骤：①  画直线，定原点

②  从原点向右(或上)的方向为正方向,从原点向左(或下)为负方向。

③  选取适当长度为单位长度。

④  在数轴上标出1、2、3、—1、—2、—3等各点。如图4所示。

2.想一想：下列各图是数轴吗？说明你的理由。

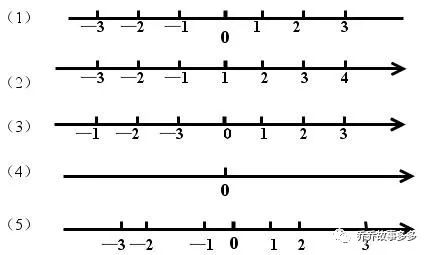
根据数轴的定义，我们可以知道：(1)不是数轴，因为没有规定正方向。(2)不是数轴，因为没有原点。(3)是数轴。(4)不是数轴，因为没有规定单位长度。(5)不是数轴，因为单位长度不等。

三、如何用数轴表示数

1.议一议：

(1)如何用数轴上的点来表示分数或小数？如：1.5，   -1.5 怎样表示。

如图6所示：

(2)所有有理数都可以用数轴上的点来表示吗

所有的有理数都可以用数轴上的点表示!

四、例题讲解

例1：在所给数轴上画出表示下列各数的点。

1，－5，－2.5,   9/2  , 0

解：如图8所示：

注意:

①把点标在线上;

②把数标在点的上方, 以便观看。

例 2 在下面数轴上，A,B,C,D各点分别表示什么数？

解：A 点表示2;    B 点表示0.25;

C点表示—0.75；D点表示—1.5。

归纳：

数轴上表示数２的点在原点的右边，与原点的距离是2个单位长度；表示－２的点在原点的左边，与原点的距离是2个单位长度．

一般地，设ａ是一个正数，则数轴上表示数ａ的点在原点的右边，与原点的距离是a个单位长度；表示－ａ的点在原点的左边，与原点的距离是a个单位长度．

五、小结

1、数轴的意义：数轴的三要素。

① 定义：规定了原点、正方向和单位长度的直线叫数轴。

② 三要素：原点、正方向、单位长度

2、数轴的画法。

3、所有的有理数都可以用数轴上的点来表示，原点右边的数是正数，原点左边的数是负数，0是正负数的分界限。

4、数形结合思想的应用。

六、练习

1.填空：

①规定了_________、________和_________的_________叫数轴。

②在数轴上，原点右边的数都是_________ 数，原点左边的数都是_________ 数。          

2.判断：

①数轴上的点只能表示整数。(    )

②两个不同的有理数，可以用数轴上同一个点表示。(    )      

③5可以用数轴上原点左边第5个单位的点来表示。(    )

3、选择：

①A、B、C在数轴上的位置如下图，则A、B、C所表示的数是

A.A、B、C都表示正数        B.A、B表示正数，C表示负数

C.A、B、C都表示负数        D.A、B表示负数，C表示正数

②在下面各图中表示数轴的是

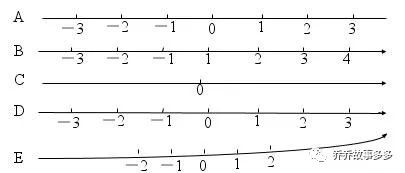
答案：1.①原点、正方向、单位长度、直线；②正，负

2.①错；②错；③错

3.①B；②D