过一点做一条直线的垂线公式_《原本》命题1.12 ——如何过直线外一点向直线作垂线？...

命题1.12

经过直线外的一点可以向直线作垂线。

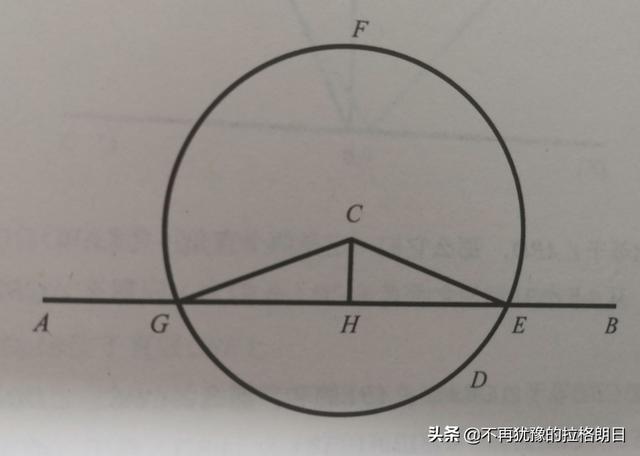
设：AB为已知直线，C点为给定的点。

求作：C点可以向AB作垂线。

在直线的另一边任取一点D，以C为圆心，CD为半径作圆EFG(公设1.3)。

公设1.3： 以定点为圆心及定长的线段为半径可以作圆。

AB与圆C交于G、E，作GE的中点H(命题1.10)。

命题1.10 一条线段可以被分成两条相等的线段。

连接CG、CH、CE(公设1.1)。

公设1.1：过两点可以作一条直线。

那么我说：CH便是C点向线段AB作的垂线。

因为：GH等于HE，CH是公共边，CG等于CE。

所以：∠CHG等于∠EHC，且它们为相邻角。

当一条线与另一条线相交形成邻角时，两角相等，皆为直角。这条线被称为另一条线的垂线(定义1.10)。

所以：CH是从C点向AB线引的垂线。

所以：经过直线外的一点可以向直线作垂线。

证完。

心得体会

之前讨论过，演绎推理是从已知条件(我们假设它是已知的或者已确定的)推导得到相应结论的过程。在这个命题的已知条件中，有任取的一点D，那么这个任取的D到底是已知条件还是未知条件呢？如果说它是未知条件，那由未知到未知的推理过程完全是无意义的。所以说，D点应该是确定的。

其实，在整个推理中，D点到底是哪个点不重要，推理中只需要利用它是“直线AB另一侧的点”这一性质即可导出整个命题的结论。换种角度来说，利用任意一个“直线AB另一侧的点”都可以得到本命题的结论。

很显然，这样的D点肯定是存在的，因为欧几里得所研究的宇宙是是由无数不可分割的点组成的，直线AB的下方更是如此。