# 定义四边形_平行四边形靶向复习一

平行四边形复习首先要理解知识关联。

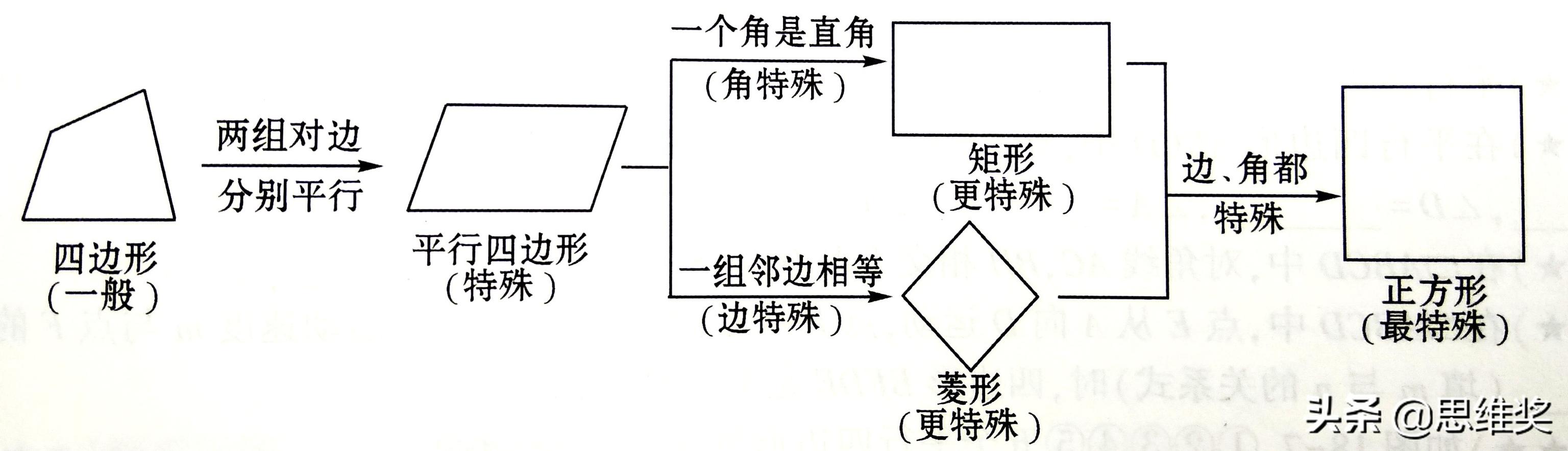
考点复习一：平行四边形和特殊平行四边形的概念及它们之间的关系

例题：有下列命题：①两组对边分别平行的四边形叫做平行四边形；②有一个角是直角的平行四边形是矩形：③有一组邻边相等的平行四边形叫做菱形；④正方形既是矩形，又是菱形；⑤矩形、菱形、正方形是特殊的平行四边形；⑥正方形不是矩形；①正方形不是菱形。其中真命题有_____。

复习考点二：平行四边形及特殊平行四边形的性质定理

研究平行四边形及特殊平行四边形的性质，主要是从边、角、对角线等方面进行研究的。

例题：1、在平行四边形ABCD中，AC，BD相交于点0，它的周长为60，若△AOB的周长比△BOC的周长少10，则平行四边形边长分别多少？

2、矩形的两条对角线相交成的锐角为60°，其较短的一边与一条对角线之和为15，则矩形的对角线长为多少？较长的一边长多少？

3、菱形ABCD的对角线AC，BD之比为3：4，周长为60cm，则菱形的面积为多少？

4、在正方形ABCD中，M是AD上的一点，ME⊥BD，MF⊥AC，垂足分别为点E.F，且ME+AMF=8cm，则AC等于多少？

复习考点三：利用图形的性质证明角相等、线段相等、线段互相平分、直线互相垂直等

例题：如图，正方形ABCD的对角线AC，BD相交于点O，E为0A上任意一点，CF⊥BE于点F，CF交OB于点C.求证：OE=OC.

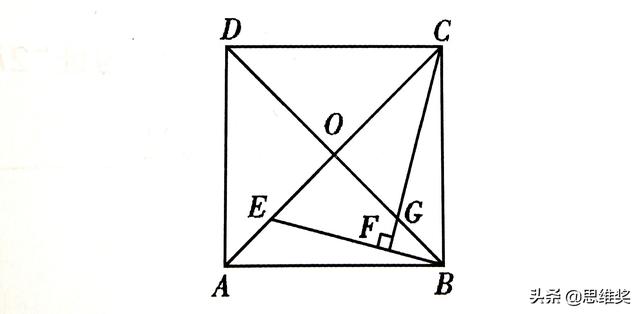
变形：如上图，正方形ABCD的对角线AC，BD相交于点O，且OE=OG。求证CG⊥BE。

复习考点四：直角三角形斜边中线的性质

例题：在直角三角形ABC中，斜边长为10cm，则斜边上的中线长是多少？

复习考点五：平行四边形及特殊平行四边形的判定定理

例题：1.如图.下列条件之一能使平行四边形ABCD是菱形的有①AC⊥BD ②∠BAD=90° ③AB=FC ④HC=BD.

2、在平面直角坐标系中，点E，F，M的坐标分别是E(-1，－3)，F(3，－3)，M(1，4).要使以E，F，M，P为顶点的四边形是平行四边形，则P点坐标应是多少？

3.某同学用四根木根搭成一个平行四边形框架，如图，已知AB=8cm，AD=6cm.现固定AB，转动AD,当∠DAB等于多少时，四边形ABCD的面积最大，此时四边形ABCD是什么形？

4、如图，用一张矩形纸片折叠成一个正方形，小明把矩形上的一个角沿折痕AE翻折上去，使AB与AD边上的AF重合，则四边形ABEF就是一个正方形，他判定的方法是什么？

复习考点六：三角形中位线定义、定理与平行四边形及特殊的平行四边形

例题：1、顺次连接一个四边形的各边中点，得到了一个矩形，则下列四边形满足条件的是什么？①平行四边形；②菱形；③矩形；④对角线互相垂直的四边形.

2、已知矩形的长和宽分别为10和8，则顺次连接矩形各边中点所得四边形是什么？其面积为多少？

3、有下列命题：①一组对边平行且一组对角相等的四边形是平行四边形：②有一个角是直角的平行四边形是矩形：③有一条对角线平分一组对角的四边形是菱形；④对角线互相垂直的平行四边形是正方形；⑤顺次连接菱形各边中点所得四边形是矩形；⑥三角形的重心是三角形三边中线的交点，其中真命题有哪些？