物体重心的特点是什么_不倒翁小姐姐为什么能摇一晚上不倒？

0 1 背景介绍

近日，西安大唐不夜城，一位身穿盛唐服装的“不倒翁小姐姐”，因其轻盈飘逸、妩媚多姿的表演成为“网红”，为了跟她“牵手”，甚至有民众将表演区的隔离栏挤坏了好几根。这位“不倒翁小姐姐”到底有何魅力呢？下面就让我们一探究竟吧。

这位“不倒翁小姐姐”在表演时，也是有她特定的演出服的，那就是盛唐时期的服饰，并且与大唐不夜城这个背景是十分契合的。去过西安的朋友都知道，大唐不夜城的夜景之美在西安甚至是全国都是非常著名的，与大唐不夜城共同被人提及到的便是大唐芙蓉园了，这两个“大唐”都是以唐朝为历史依据的，这位“不倒翁小姐姐”在大唐不夜城身着唐朝服装，化上唐朝时的女子妆容，精彩多姿的表演，让人一瞬间仿佛梦回大唐。

不倒翁是一种历史悠久的玩具，特别受到各个年代儿童们的喜爱。清代文人魏崧在《壹是纪始》写到：“不倒翁始于唐。”他据《唐摭言》中的记载：“卢连举不第，赋《酒胡子》长篇以寓意，序日：‘巡觞之胡，旋转由人。’今谓之不倒”，这便是不倒翁的最初模型。而后渐渐流传至今，演变成为哄逗幼儿的玩具，给儿童乃至大人们增添了无穷乐趣。那么,我们学习了《工程力学》之后，来较为确切的从力学上来分析不倒翁的原理，并了解其在日常生活生产中的相关应用。

0 2 力学原理

最常见的不倒翁是纸身、泥底，即用纸浆灌模或用废纸粘糊成形，再用泥土制成半圆形的底座，将二者粘合好之后，再在外表糊上净纸，施以彩绘而成；也有的用木头做底，底部中心固定上铁块和小石子；还有用小葫芦挖净内瓤，内部灌铅做成的“葫芦”；今天还有用鸡蛋壳、旧乒乓球做成的小不倒翁。所有的这些不倒翁都有相同的特点：上半身为空心壳体、下半身是一个实心的半球体，底部为圆形。这些特点使它们具有了一致的基本力学结构，都能达到“不倒”的效果。

1大唐不倒翁的形体结构

我们假设大唐不倒翁上半身为空心壳体，重量很轻；大唐不倒翁的下半身是一个实心的半球体，重量较大，大唐不倒翁的重心就在半球体之内。下面的半球体和支承面之间有一个接触点，这个半球体在支承面上滚动时，接触点的位置就要发生改变。大唐不倒翁始终用一个接触点站立在支承面上，它永远是一个独脚体。

2大唐不倒翁平衡的稳定性

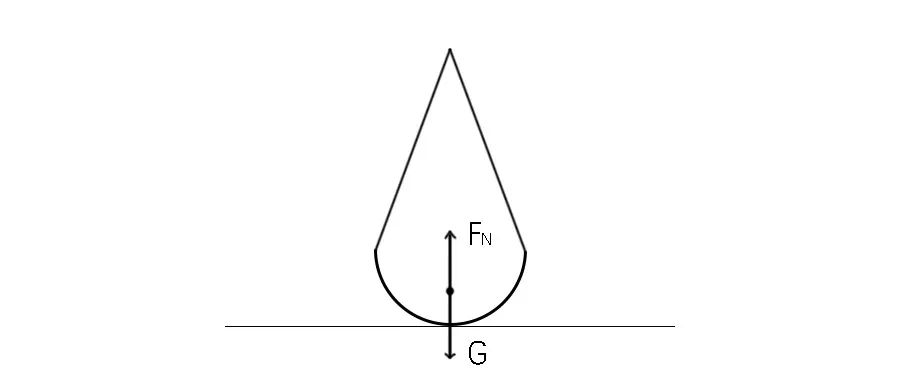
大唐不倒翁在受到外力的作用时，就要失去平衡，而在外力去除后，大唐不倒翁能自行回复到平衡状态，这说明大唐不倒翁具有一种抵抗外力干扰保持平衡的能力，这就是平衡的稳定性。这种抵抗干扰保持平衡的能力的形成，应该从大唐不倒翁的受力情况来看。

3大唐不倒翁的受力情况有三种

① 大唐不倒翁平衡的受力情况：

大唐不倒翁在地面上，受到两个外力的作用：一个是重力G，地球对大唐不倒翁的吸引力；另一个是支持力，桌面对大唐不倒翁底面半球体的反作用力。根据物体的平衡条件，只要这两个力大小相等、方向相反、作用在一条直线上，大唐不倒翁就能够保持平衡的状态。

假设受外力时，大唐不倒翁重心为O，接触点为C，重力为G，倾斜了α角度，F到C点距离为m，AO,OC分别为l和d 。

② 大唐不倒翁倾斜的受力情况：

当大唐不倒翁受到外力时，外力产生的干扰力矩，重力形成一个抵抗力矩，干扰力矩为：M1=F*m，抵抗力矩为：M2=Gcosθ*d

此时两个力矩方向相反，且随着大唐不倒翁倾斜的角度α不断增大，重力作用线G的偏移量也不断增大，抵抗力矩M2即Gcosθ*d的值也不断增大，当抵抗力矩M2等于干扰力矩M1时，大唐不倒翁就进入新的平衡状态——倾斜的平衡状态，此时外力的干扰作用也就宣告停止。

由此可知，大唐不倒翁受到外力干扰后，原有的平衡破坏了，但新的平衡随之形成，大唐不倒翁可以接续地保持平衡，虽然平衡的方式不同，但平衡的本质不变，这种便是动态平衡。此时大唐不倒翁不倒。

③大唐不倒翁复原的受力情况：

(1)从势能角度考虑，势能低的物体比较稳定，物体一定会向着势能低的状态变化。当大唐不倒翁倒下的时候，由于集中了大部分重心的底座被抬高，造成势能增加，所以大唐不倒翁要回复原来的位置。

(2)从杠杆原理来说，大唐不倒翁倒下时，重心的作用点一直处于端部，不管支点在哪里，虽然底座的力臂较短，但是力矩＝力＊力臂，大唐不倒翁还是会因为底座那头力矩大而回复到原来位置。如本例中，去掉外力后仍有力矩M2，力矩M2使得大唐不倒翁恢复到一开始的平衡位置。

(3)大唐不倒翁底部为圆形，摩擦力小，便于大唐不倒翁回到原来位置。

在以上的整个过程中，建立新的平衡是其中主要的问题，因为只有如此才能抵制外力的干扰，而恢复原有的平衡则是次要问题，因为此时外力的干扰已经去除。在整个过程中不倒翁始终保持平衡的属性，这便是“平衡的稳定性”。

4力学原理小结

综上所述，这个原理的要点在于：使重力的作用线偏离支点，使重力对支点产生力矩，即抵抗力距。由于大唐不倒翁倾斜的角度不断增大，重力作用线的偏移量随之增大，抵抗力矩也随之增大，最终实现和外力力矩的平衡，大唐不倒翁抵抗外力干扰、保持平衡的能力就是这样形成的。

03 大唐不倒翁仿真模拟 基于好奇心驱使小数对大唐小姐姐进行了仿真模拟。 假设底座半圆半径   m，质量   kg，初始角度为  ，模拟步长   s。模拟的主要步骤如下：

• 根据角速度更新角度：
• 根据角加速更新角速度：，其中角加速度  由运动方程给出。
• 确定半圆圆心  的水平位置：x = πθr/180
• 根据半圆圆心  的水平位置，以及半圆的转动角度，确定半圆位置。
• 更新时间 。如果  晚上，结束，否则跳到第 1 步。

为了模拟视觉效果，首先需要画一个半圆和一个性感的小姐姐。

为了将小姐姐妙曼的身姿展现得淋漓尽致，那大长腿，那伸出的纤纤玉手 ······小数“安排”了一下插画师，让他加了亿点点细节。

根据运动方程，算出某时刻半圆心的位移以及角度后，需要对半圆和小姐姐进行平移和旋转。平移容易，旋转可根据以下公式进行。

模拟结果如下，小数表示很满意~(模拟细节完整代码请在校苑数模公众号会话窗口回复【不倒翁】获取)。

世人谓我恋长安，其实只恋长安某。

你愿意为了这位“不倒翁小姐姐”

再回长安吗？

部分图片来源于网络 部分内容转载自微信公众号“数学模型”

在看点这里