各位同学们经过上几期的内容,叶老师已经将三角系列的知识以及考点全部讲解完毕了,大家可以回顾一下: ①《由浅入深,化角为弧,助你了解高考三角函数二三事 》
②《高三同学要注意,背诵三角恒等公式还不够,承上启下作用要突出 》
③《高三同学看过来,弄清这些正余弦定理疑难点,便可打好大题第一战 》
④《高三同学看过来,学好正余弦定理的应用,为三角系列划上完美句号》
今天叶老师将按照考纲顺序,继续为大家讲解平面向量的有关内容,希望对大家能够有所帮助。
作者简介:叶老师,笔名“动人定理”,专职教师,数学学科研究员,目前担任机构数学教研组组长及学生学业规划师。曾供职合作于多家上市教育公司,对中高考数学考点有着深入认知与理解。拥有超过10000小时的高三毕业班学生一对一辅导经验。

平面向量
导读
不知道同学们还记不记得,叶老师之前借着学生问过的一个问题写了一篇如何学好平面向量的文章
《高三同学必看,单纯记概念向量学未必学的好,联立思维是关键》,大家可以回顾一下。回顾之后,今天叶老师将分为知识点回顾以及经典题型总结两个方面,为大家具体讲一下平面向量在高考中的应用,让大家彻底突破平面向量系列考点,为各位高三同学高考数学的超常发挥尽一份绵薄之力!
一、平面向量的知识点回顾
1.平面向量的有关概念
①向量:既有大小又有方向的量叫做向量,向量的大小叫做向量的长度(或模).
②零向量:长度为0的向量,其方向是任意的.
③单位向量:长度等于1个单位的向量.
④平行向量(共线向量):方向相同或相反的非零向量.平行向量又叫共线向量.
规定:0与任一向量平行.
⑤相等向量:长度相等且方向相同的向量.
⑥相反向量:长度相等且方向相反的向量.
PS:互为相等向量或者相反向量的两个向量长度必须相等
2.向量的线性运算
向量的线性运算主要分为:加法,减法以及数乘运算,具体法则我们以下列表格为准:

向量线性运算具体规则
同学们在掌握好上述的运算法则前提下,可以额外拓展一些内容,具体如下:

拓展内容
3.平面向量的共线定理
①判定定理:a,b是两个非零向量,若存在一个实数入使得b=入a,则向量b与a共线
②性质定理:若向量b与非零向量a共线,则存在唯一一个实数入,使得b=入a
注意:只有非零向量才能表示成与之共线的其他向量,并且在表示的过程中要注意待定系数法和方程思想的运用。
4.平面向量的基本定理

平面向量的基本定理
简断截说:平面内任何一个向量都可以用一组基底唯一表示。
另外大家还必须着重于这样一种特殊情况:如果,OA=入OB+uOC,那么当A,B,C三点共线的时候则有
入+u=1。这个结论常在考试中涉及。
5.平面向量的数量积及其应用
(1)向量的夹角
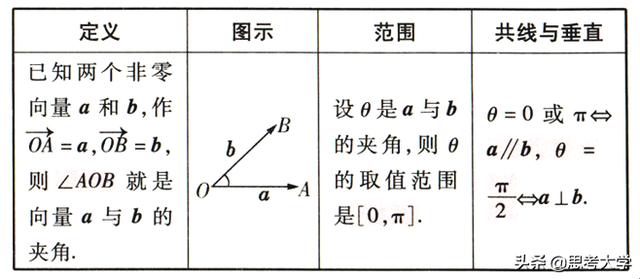
向量的夹角
PS:两个向量只有平移到相同起点后,才可以开始测量或者计算夹角
另外同学们也得记住如何利用向量判断一个三角形的形状

(2)平面向量的数量积与投影

注意:投影和两向量的数量积都是数量,不是向量。
(3)平面向量数量积运算律

6.平面向量的坐标运算
(1)坐标表示及运算法则

坐标运算
(2)平面向量数量积与向量坐标之间的联系

7.三角形“四心”与向量之间的关系

二、平面向量常考重点题型总结
1.用基底向量表示一个未知的向量

例题
分析:此类型的题目往往图形较为复杂,就拿这题来说,同学们需要先将CE向量利用三角形法则用与之相邻的AC和AE两个向量表示出来。通过观察发现题目中的四个选项都含AB和AC向量,因此我们得利用题目中已经有的数量关系,尽可能地将CE的表达式往AB与AC方向上靠拢。
下面我们具体来看一下解析过程:

解析过程
小结:通过这道题目我们总结一下做向量基底表示的题目需要注意的地方:
①一开始应先利用三角形法则将未知向量用与之相邻的两个向量表示出来,然后再去绕
②观察题目选项很重要,因为题目中的选项便决定了这道题应该要用哪对基底。
2.以向量的夹角与模长为背景的题目

例题
分析:此类题目往往以向量的夹角与模长以及投影为背景,以本题为例,同学们在做的时候可以先画出示意图,这样不会乱了方向,然后根据示意图先把题目中要求的东西的表达式表达出来,然后利用已有条件一步步地将表达式中的量求出来,最后得出结果。
下面我们具体来看一下解析过程:

解析过程
小结:在解此类题目的时候我们应该注意如下几点:
①一定要注意是谁在谁方向上的投影,最好画出示意图,不然容易乱了方向。
②在求解类似|a+b|,|a-b|的时候,可利用完全平方公式,不过要注意平方的时候注意夹角,并且 最后要记得开方。
3.平面向量的基本定理中的特殊情况——三点共线的考察

例题
分析:在做此题的过程中,同学首先得观察图中的C,F,D三点共线。然后利用题目中的条件,以及三点共线向量的联立去求解。
下面我们来看一下具体的解析过程:

解析过程
小结:对于此类题目,叶老师认为,最关键的有两点:
①观察:图中具体哪三点共线,这样便于构造三点共线向量表达式
②联立:一定是把题目中已经有的向量表达式,利用向量间的数量关系,想办法转化到“三点共 线”的表达式中去,因为在三点共线的向量表达式中,基底的系数和为定值1。
4.利用平面直角坐标系解决平面向量问题
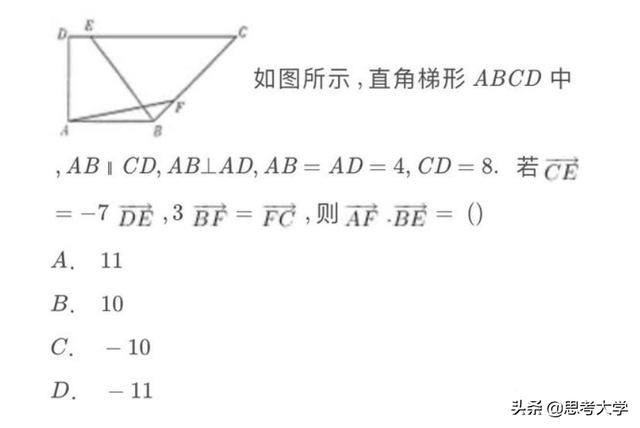
例题
分析:本题中所给的图形是直角梯形,并且边的条件给得挺多,因此可以采用建立平面直角坐标系的方法将A,F,B,E四个点的坐标都表示出来,然后利用向量的坐标运算便可算出结果。
下面来看一下具体的解析过程:

解析过程
小结:做此类题目主要还是看题目中给的图形的形状,当题目中出现比较规则的图形(等腰等边三角形、正方形、菱形、直角梯形等)的时候可以考虑用向量的坐标运算去求解,这样非常方便快捷。
5.三角形的四心与向量的结合问题
根据叶老师往期经验,三角形的外心与重心与向量结合的题目考得频率较高,因此叶老师将各举一例向大家说明一下该如何做此类题目
(1)三角形外心与向量的结合问题:
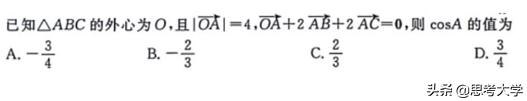
例题
分析:此时可以画出示意图,根据三角形外心的性质,我们可以得知,在图中线段OA,OB以及OC的长度相等,换句话说也就是:向量OA,OB,OC的模长相等。另外我们还可以利用外心的性质推断出∠BOC=2∠A,这个条件,对解题提供更有力地说明。
下面来看一下具体的解析过程:

解析过程
小结:在做三角形外心与向量结合的题目时,大家应该牢牢把握住三角形外心的两个性质: ①OA=OB=OC ②∠BOC=2∠A,然后再利用题目中的条件,将OA,OB和OC三个向量的线性关系表示出来,之后对式子的左右两边同时平方,然后利用向量的夹角公式,结合三角恒等变换公式求出结果。
(2)三角形重心与向量的结合
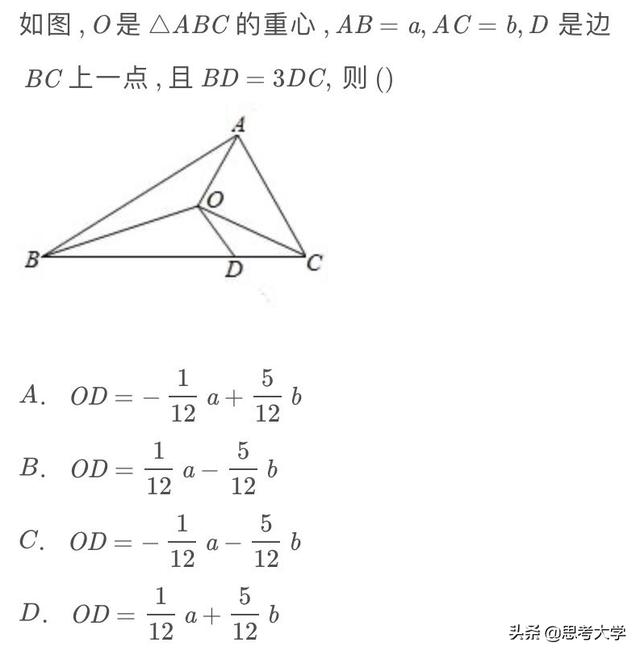
例题
分析:做三角形重心与向量结合的题目也需要画出示意图,并且在适当地情况下需要对线段进行延长,这样可以构造中点,并结合三角形重心的性质进行计算,这样更加方便可行。
下面请看具体的解析过程:

解析过程
小结:三角形重心与向量的结合题目,叶老师认为主要还是以三角形重心的性质为主,然后结合题目中的数量关系,有时适当地延长线段便可构造中点,最后便可相对轻松地算出答案。
在文章的结尾,叶老师想对向量最后总结几点:
①在做向量基底运算的时候联立思维很重要。
②向量的模长、夹角以及投影这三个方面联系得非常紧密,同学们可以多做做此类型的题目
③三角形的四心与向量的联系比较多,大家有空的时候可以画画图,去证明一下相关的结论
④直角坐标系对于向量问题的帮助很大,它可以解决向量的夹角问题。
最后希望大家都能突破平面向量的知识点,最后都能考出好成绩!
欢迎大家关注【思考大学】,
如果觉得今天的文章对大家有帮助,请你点个赞!
也把欢迎大家在文末留言,你们想学习的知识告诉我~
你的认可,是我们努力的方向!






 本文总结了高三考生必备的平面向量知识点,从概念回顾、线性运算、共线定理、基本定理、数量积应用到常考题型,包括向量表示、夹角问题、三点共线和坐标运算,助力高考数学突破
本文总结了高三考生必备的平面向量知识点,从概念回顾、线性运算、共线定理、基本定理、数量积应用到常考题型,包括向量表示、夹角问题、三点共线和坐标运算,助力高考数学突破

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








