01
知识框架
02
知识点详解1
B树
①定义与性质
B树也叫B-树 。B树是一种平衡的多分树,通常我们说m阶的B树,是二叉排序树的一种扩展,它必须满足如下条件:01
每个结点最多只有m-1个关键字。
02
根结点最少可以只有1个关键字。
03
非根结点至少有m/2个关键字。
04
每个结点中的关键字都按照从小到大的顺序排列,每个关键字的左子树中的所有关键字都小于它,而右子树中的所有关键字都大于它。
根结点的关键字数量范围为[1,m-1]; 非根结点的关键字数量范围为[m/2,m-1];②B树的插入
在进行B树的插入时,根据上面提到的B树的性质,我们可以总结出一条准则: 在向B树插入结点时,先判断当前结点关键字的个数是否小于等于m-1,如果满足,直接插入即可,如果不满足,将结点的中间的关键字将这个结点分为左右两部分,中间的结点放到父结点中即可。 下面我们来看具体的例子: Q:向一颗5阶B树中插入关键字A:5阶B树中,每个结点最多有4个关键字,最少有2个关键字(根结点除外)。01
插入15,30,45,60

02
插入19,此时该结点的关键字个数大于,需进行分裂

03
插入20,25,28

左边结点的关键字数大于4,分裂

③B树的删除
B树的插入比插入稍复杂些,只要牢记B树应该满足的条件,就能够解题。 下面我们来看一个B树删除关键字的例子:
01
删除19,19所在结点所剩关键字个数大于2,则可以直接删除

02
删除30,30不是叶子结点,不能直接删除。这种情况的规则:30是非叶子结点,对于非叶子结点的删除,我们需要用后继的关键字覆盖要删除的关键字,然后在后继关键字所在的分支中删除该关键字。对于删除30,需要将后继元素32移到被删除的30所在的结点。




03
删除40,删除后不满足B树要求。需要考虑向兄弟结点借元素,但兄弟结点也没有多的结点(2个),借不了。若遇到这样的情况,还是将先将父结点的元素移到该结点,然后,将当前结点及它的兄弟结点中的关键字合并,形成一个新的结点。

再与兄弟结点合并
2
B+树
①定义与性质
B树与B+树有很多相似之处:01
根结点所含关键字范围:1 <= k <= m-1
02
非根结点所含关键字范围:m/2 <= k <= m-1
不同点:01
B+树有两种类型的结点:内部结点(也称索引结点)和叶子结点。内部结点就是非叶子结点,内部结点不存储数据,只存储索引,数据都存储在叶子结点。
02
内部结点中的关键字都按照从小到大的顺序排列,对于内部结点中的一个关键字,左树中的所有关键字都小于它,右子树中的关键字都大于等于它。叶子结点中的记录也按照关键字的大小排列。
03
每个叶子结点都存有相邻叶子结点的指针,叶子结点本身依关键字的大小自小而大顺序链接。
04
父结点存有右孩子的第一个元素的索引。
下面我们来看一颗B+树,感受一下它和B树的区别。
②B+树的插入
B+插入操作很简单,掌握一个要点即可: 当结点关键字数量大于m-1的时候,按中间关键字分裂成左右两部分,中间关键字分裂到父结点当做索引存储,但是,中间的关键字自身还是分裂右边结点这一部分的。 下面给大家举一个B+树的插入例子: 向一颗5阶的B+树中插入元素。 分析:5阶B+树的结点中最少2个关键字,最多4个关键字。01
插入10,16,22,28

02
插入30,此时该结点的关键字数量大于4个了,进行结点分裂

03
接着插入35,39,结点继续分裂


③B+树的插入
对于删除操作是比B树简单一些的, 由于叶子结点有指针的存在,向兄弟结点借元素时,不需要通过父结点了,而是可以直接通过兄弟节移动即可(前提是兄弟结点的元素大于m/2),然后更新父结点的索引;如果兄弟结点的元素不大于m/2(兄弟结点也没有多余的元素),则将当前结点和兄弟结点合并,并且删除父结点中的关键字。 下面我们来看一个例子: 初始状态B+树: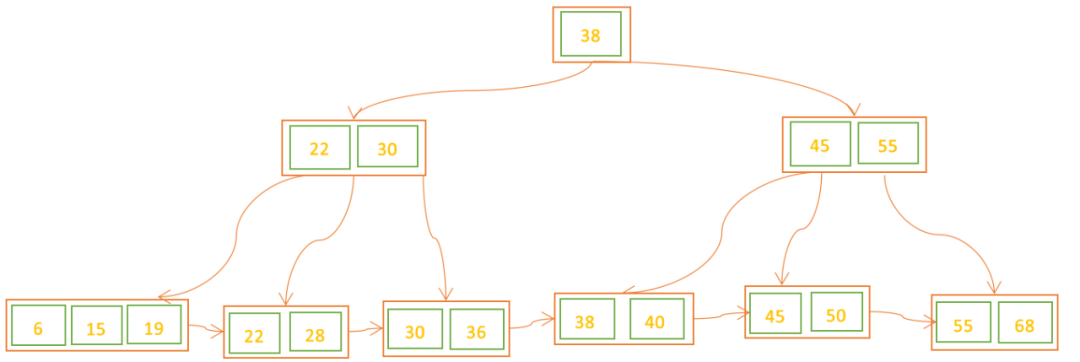
01
删除22,删除后,发现B+树不满足要求,且左边兄弟结点的关键字个数够借,借关键字后再修改父结点索引。
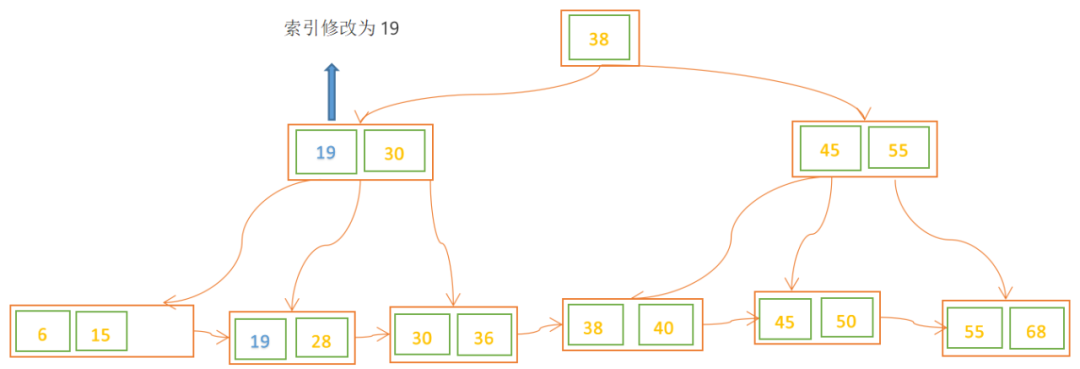
02
删除元素28,发现B+树不满足要求,并且发现左右兄弟结点都没有多余的关键字可借,此时选择与其兄弟结点合并再修改父结点索引。
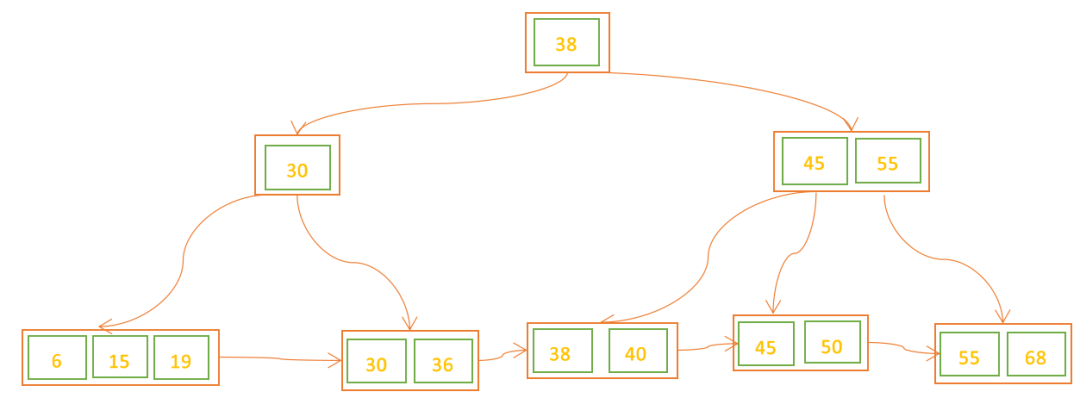
此时,其父结点(30)也不满足B+树条件,故将结点30与其兄弟结点进行合并

03
相关习题01
(2012年统考)已知一棵三阶B树,如下图所示删除关键字78得到一棵新B树,其 最右叶结点中的关键字是()

A、60
B、 60, 62
C、62, 65
D、65
(点击选项查看答案) Tips: 根据B树应满足的条件以及删除B树结点的准则即可解题。02
(2016年统考)B+树不同于B树的特点之一是()
A、能支持顺序查找
B、 结点中含有关键字
C、根结点至少有两个分支
D、所有叶结点都在同一层上
(点击选项查看答案) Tips: B+树的叶结点包含了全部关键字信息,且按大小排列,故B+树支持顺序查找。B树只支持多路查找。03
(2018年统考)高度为5的3阶B树含有的关键字个数至少是()
A、15
B、31
A、解放思想
B、与时俱进
C、实事求是
D、持续稳定
进
C、62
D、242
(点击选项查看答案) Tips:3阶B树的非根结点所包含的关键字个数最少是2个,而根结点最少包含1个关键字,这样的树型相当于一棵高度为5的满二叉树,利用公式计算出其包含的关键字个数最少是31。计算机考研qq群
总群:625590924
广大:1143982604
暨大:1071137230
广工:938111325
华工:428389734
深大:729770764
浙大:978938582
厦大:1125268501
中大:921801084
南航:281118241
华农:515681663
重邮:736197896
北邮:1126650806
南邮:1109929146
广外:976231252
东北大学:1128523098
华南师大:428389734
南昌大学:923249141

给个“在看”支持一下我







 本文详细介绍了B树和B+树的定义、性质,包括每个结点的关键字数量限制和排序规则。重点阐述了B树的插入、删除操作,如关键字的分裂与合并。同时,讨论了B+树的特点,如叶子结点的链接结构,以及B+树的插入和删除操作。最后,通过几道计算机考研题目展示了相关知识点的应用。
本文详细介绍了B树和B+树的定义、性质,包括每个结点的关键字数量限制和排序规则。重点阐述了B树的插入、删除操作,如关键字的分裂与合并。同时,讨论了B+树的特点,如叶子结点的链接结构,以及B+树的插入和删除操作。最后,通过几道计算机考研题目展示了相关知识点的应用。
















 685
685

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








