四阶行列式计算_从三阶到n阶，为什么不好好讲讲四阶行列式

注：为什么n阶行列式那样定义，请看本文！

3.1四阶行列式的对角线法则推广

我：“我们已经知道了二、三元线性方程组的行列式解法，对于四元线性方程组是不是可以用同样的解法呢？我们要先解决两个问题，一个是四阶行列式的运算，能否使用对角线法则？二是四元线性方程组能否用上述行列式方法来解。下面我假定四元线性方程组也使用对解线法则来运算，验证一下能否用来解线性方程组。”

3.2四阶行列式的另一种推广方法

      小明：“刚学到一个方法就被否定，感觉真不好！”

小慧：“我们可以从二、三阶行列式的定义入手,再分析分析，我觉得四阶行列式不能这样简单推广,一定还有别的推广方法。或许别的方法下行列式解法还可以用呢。”

    小慧：“我来分析一下二、三阶行列式的特点。”

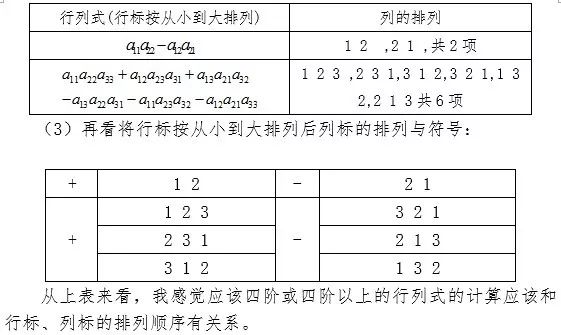
小慧分析的还真是头头是道。

我：“课本上确实讲到排列和逆序数了，我们一块来学习一下。”

【李老师】主题：排列与逆序数

定义 全排列:把n个不同的元素排成一列，叫做这n个元素的全排列，简称排列。

如3个不同元素 1,2,3的所有可能排列有：

例：求排列53214的逆序数.

解：规定标准顺序为12345,考虑到53和35是一个逆序，只计算每一个元素前面比它大的元素的个数, 那么一个排列逆序数的计算方法是求每个元素前面比它大的元素数之和。

5有0个，3有1个，2有2个，1有3个，4有1个，故逆序数为7.

定义 奇排列和偶排列： 逆序数为奇数的排列称为奇排列，逆序数为偶数的排列称为偶排列。

对换：在一个排列中，将任意两个元素对调，其余元素不动，这种作出新排列的手续叫做对换．若对换的是相邻的两个元素，则称为相邻对换．

定理：一个排列中的任意两个元素对换，排列奇偶性改变。(证明略)

推论  奇排列调成标准排列的对换次数为奇数，偶排列调成标准排列的对换次数为偶数．【/李老师】

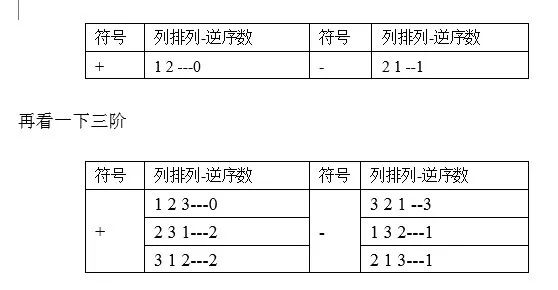
我：“知道了这些知识点，再回过头来看看二、三阶行列式中每一项符号的判断,先看二阶.”

原创文章，禁止转载！