信号与系统sa函数求积分_为什么说欧拉是继承了莱布尼茨的微积分原理

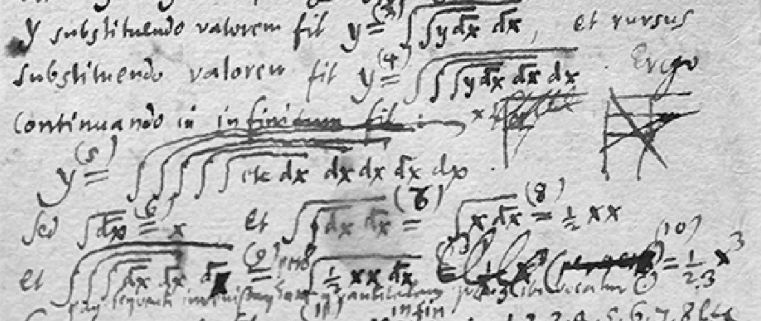
先请出我们今天的两大主角：莱布尼茨和欧拉。

学过微积分的人对莱布尼茨这个名字并不陌生。而大家可能不知道的是莱布尼茨在到巴黎担任外交官之前还是一个被认为对“阅读冗长的数学证明”缺乏耐心的新手。他不满足于自己的知识，下定决心，大力填补自己的缺口，大量阅读令人景仰的数学家们的著作，远至欧几里得，近至他那个时代的帕斯卡、巴罗还有他一度师从的惠更斯。开始的时候困难中重重，但是，有志者事竟成，在几乎狼吞虎咽地吸收了同时代人的成果之后，莱布尼茨把他们远远地抛在了后面，创造了微积分。

莱布尼兹（Gottfriend Wilhelm Leibniz,1646-1716）

由于莱布尼茨不像牛顿，他广泛与许多数学家通信，讨论新分析学这一学科，以求恰当的符号和表达形式，于是成长了一批这一学科的爱好者，著名的有伯努利兄弟和大数学家欧拉。

莱昂哈德·欧拉（Leonhard Euler1707年4月15日-1783年9月18日）

欧拉这个人相信对数学有所接触的小伙伴们都知道，可以称之为史上最高产的数学家，数学界在1911年开始出版他的著作集《欧拉全集》，这本身就是一个巨大的挑战，这个耗费了将近一个世纪的时间的庞大的出版项目充分证明了欧拉与生俱来的过人的数学天赋。其中就有厚厚的18卷将近9000页是论述分许学的，包括函数（1748）、微分学（1755）和积分学（1768）的里程碑式的教材，以及数十篇题材从微分方程到无穷级数以致椭圆函数论的论文。

莱昂哈德·欧拉在1783逝世的时候，距离莱布尼茨发表第一篇微积分论文一百周年仅差一年。而欧拉与莱布尼茨的微积分原理之间关系绝不是这么简单。今天我们就来看看为什么说欧拉继承的莱布尼茨的微积分原理。

莱布尼茨的部分数学手稿

01莱布尼茨的观点

要说函数一词，最开始是由莱布尼茨首先采用的，在他1673年的一部手稿中用到了function一词，表示任何一个随着曲线上的点变动而变动的量的纵坐标。用

表示相邻的序列之差，后通过插入法变为表示相邻x间的差。在此基础上定义

为函数的微分，给出了其加减乘除根式高阶无穷小的运算规则：

如果

是给定的常数，则

，

；

加法和减法：如果

，则

；

乘法：

，

;

除法：

；

幂：

，另一方面整数幂的运算规则既适用于复数，也适用于根式；

高阶微分：

;

1676年，莱布尼茨意识到求切线的最好方法是求

通过割线逼近）。同时给出了求极值和拐点的条件。在

求面积问题上 ，莱布尼茨认为曲线下的面积是由非常多小矩形面积之和，他定义了求和符号。求球的表面积，利用特征三角形，每一边都分化为微分量（无穷小）。

莱布尼茨认为当

是一个无穷小量时，如

，

这样的

的任意次幂将是更小的量，可以忽略。用他的原话来说就是“考虑这样一种无穷小量将是有用的，当计算他们的比的时候，不把它们当做零，但是只要它们与不可比较的大量一起出现时，就把它们舍弃。例如如果我们有

，就把

舍弃。”

他觉得微积分作为一种运算方式，是不用解释而自明的。他不想如帕斯卡那样，把无限小看作神秘之物，也不用几何直观去加以澄清。如他自己所说的，他仅仅诉诸智力，更强调这种方法的运算性质。在这种意义上，他也许可以确当地被称为在数学上相对于直觉主义的形式主义的奠基人。他相信，假如他清楚地给出了适当的运算规则，并且把它们应用得恰当，就一定会得到某种合理

02欧拉的观点

欧拉的许多前辈们认为微积分学是与几何结合在一起的，但是欧拉使这一学科成为了一种形式的函数的理论，因而就无需回到几何图形，或几何概念上去了。莱布尼茨用函数这个词有些像我们今天的用法，并自夸他的无限小法，并不只限于代数函数，如同笛卡尔那样，也同样适用于对数和指数函数。然而欧拉是突出函数的概念，并对全体初等函数连同它们的微分和积分进行了系统的研究和分类的第一个数学家。

他把函数定义为由简单符号表示出来的某些常量和变量的解析表达式所表达的量，他认为函数的本质是一种形式上的表示，而不是概念上的关系承认。

对于无限小和无限大，欧拉并不认为它们是什么了不起的神秘特性。欧拉认为无限小就是零，但却存在着“不同阶的零”，也就是不同阶的无限小，而“无限小演算只不过是不同无限小量的几何比的研究。对于

和

，他反对数学原子论或单子论，怒斥其为“对充足理由律的拙劣歪曲”，认为小于任何指定量的数必然是一个零，因此

和

就是零。因而

微分就是求消逝的增量之比，求

的一种富有启发性的方法。

03欧拉继承了莱布尼茨微积分原理什么内容

我们不妨概述一下，思考前面的问题。欧拉他们为什么说是继承了莱布尼茨的微积分原理？我们看，继承了什么东西。

1、 把无穷小或微分作为基本研究对象。承认积分是微分的逆过程。

2、 都把略去高阶无穷小作为一种处理手段。

3、 把导数看成微商。

不同之处在于对无穷小量的理解。

这样，我们便很好回答欧拉对不同阶的零的认识，以及不同阶的零与莱布尼茨的

的关系。事实上不同阶的零都是

，相对于低阶的

，高阶的

更小，可以随意丢弃。不同阶的零相当于莱布尼茨的

的高阶次方，欧拉对于微积分原理的关注点在于

应用，他把研究的重点放在了 正规的函数上，在实际问题中把微分当作

来处理。