matlab用relu函数优化逻辑回归_深度学习(4): 深度学习基础1——激活函数和损失函数...

目录

1 激活函数

2 损失函数

参考资料

1 激活函数

首先来看激活函数在神经网络模型中的位置，如下图所示的激活函数实际上隐藏在神经网络模型中的连接线上。前文反复强调神经网络模型中的连接是最重要的，该连接线包括输入矩阵与权值矩阵相乘的过程，还包括激活函数对数据进行激活的过程。

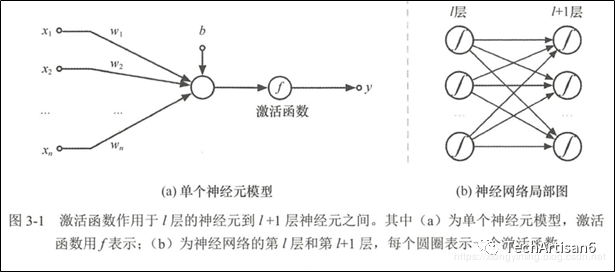
激活函数的一般性质

(1) 单调可微一般情况下，我们使用梯度下降算法更新神经网络中的参数，因此必须要求激活函数可微。如果函数是单调递增的，求导后函数必大于零(方便计算)，因此需要激活函数具有单调性。

(2) 限制输出值的范围输入的数据通过神经元上的激活函数来控制输出数值的大小，该输出数值是一个非线性值。通过激活函数求得的数值，根据极限值来判断是否需要激活该神经元 。也就是说，我们可以通过激活函数确定是否对一个神经元的输出感兴趣。

(3) 非线性因为线性模型的表达能力不够(从数据输入到与权值求和加偏置，都是在线性函数内执行权重与输入数据进行加权求和的过程，如( )，因此激活函数的出现还为神经网络模型加入非线性因素。激活函数拥有上述特性，它存在的核心意义在于：一个没有激活函数的神经网络只不过是一个线性回归模型，它不能表达复杂的数据分布。神经网络中加入了激活函数，相当于引入了非线性因素，从而解决了线性模型不能解决的问题。

选择不同的激活函数对神经网络的训练和预测都有着不同程度的影响，下面来分析神经网络中常用的激活函数及其优缺点。

1.1 线性函数

线性(Linear)函数是最基本的激活函数，其因变量与自变量之间有直接的比例关系。因此，线性变换类似于线性回归。实际上，在神经网络中线性变换，意味着节点按原样通过数据信号通常与单层神经网络一起使用。

代码示例

import matplotlib
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.mlab as mlab
import math

# 线性函数定义
def Linear1(x, W=1.5):
    return W*x

x = np.arange(-2, 2, 0.01)
y_linear1 = Linear1(x)

plt.plot(x, y_linear1, color = '#1797ff',linewidth=3)
ax=plt.gca()
ax.set_xlim([-2, 2])
ax.set_ylim([-2, 2])
ax.axhline(0, linestyle='--', color='gray', linewidth=1)
ax.axvline(0, linestyle='--', color='gray', linewidth=1)
plt.title("Linear")
plt.show()

结果如下

1.2 Sigmoid函数

Sigmoid 函数是一种在不删除数据的情况下，减少数据的极值或异常值的函数。因此，它能够很好地表达激活的意思，未激活值为0，完全饱和的激活值则为l。在数学上，Sigmoid 激活函数为每个类输出提供独立的概率。表达式如下：

(1) Sigmoid函数优点

1. Sigmoid 函数的输出映射在［0,1］范围内，函数单调连续，且输出范围有限制，优化稳定;
2. 易于求导；
3. 输出值为独立概率，可以用在输出层.

(2) Sigmoid函数缺点

1. Sigmoid 函数容易饱和，导致训练结果不佳：
2. 其输出并不是零均值，数据存在偏差，分布不平均.

代码示例

import matplotlib
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.mlab as mlab
import math


# sigmoid 函数定义
def sigmoid(x):
    return 1 / (1 + np.exp(-1*x))


x = np.arange(-2, 2, 0.01)
y_sigmoid = sigmoid(x)

plt.plot(x, y_sigmoid, color = '#1797ff', linewidth=3)
ax=plt.gca()
ax.set_xlim([-2, 2])
ax.set_ylim([-1, 1])
ax.axhline(0, linestyle='--', color='gray', linewidth=1)
ax.a