若矩形截面梁的高度和宽度_求解矩形截面梁横力弯曲变形横截面上切应力

​矩形截面梁发生横力弯曲变形时，求解横截面上切应力的思路和方法很值得研究和学习，现将其中需要了解的注意事项归纳如下：

1）问题引出

如图所示，梁发生横力弯曲变形，取出微段dx作为研究对象，求截面m1n1内距中性轴为y的横线上的切应力。

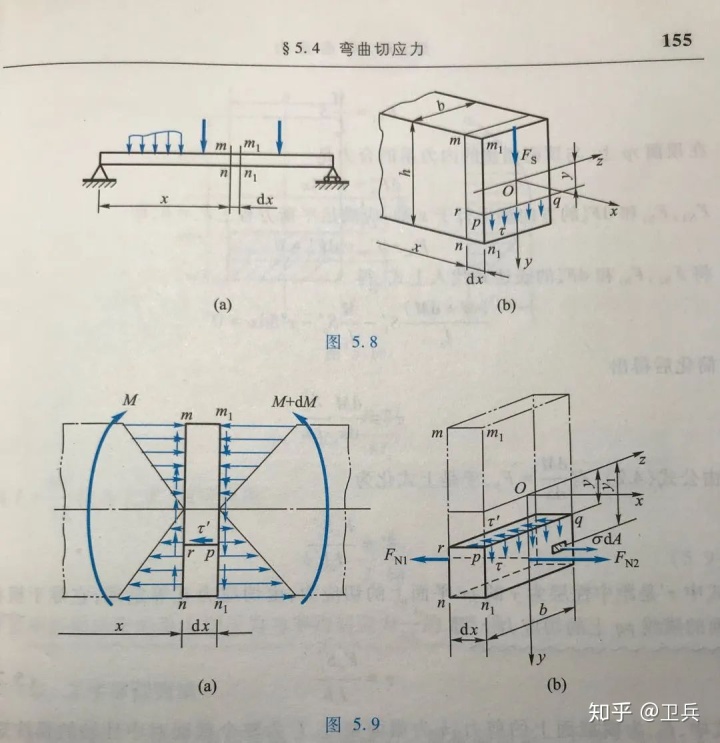
2）前提假设

（1）假设横截面上各点切应力的方向都平行于剪力；

（2）由于沿截面宽度方向材料特性、截面特性、变形特点都没有差异，所以假设切应力沿截面宽度方向均匀分布；

3）关键思路

（1）求应力的常见思路之一，就是将应力汇总成力，然后根据受力平衡条件先解出力，再进一步求解应力；

（2）注意，应力永远不能列平衡方程；

（3）凡是讨论切应力的问题，都不要忘记切应力互等定理，不论是求值还是确定方向，该定理都能带来启发。

（4）本来要求pq这条线上的切应力，但是却不能直接求，而要通过求这条线所在的水平面上的切应力间接求解。这样作的原因和合理性如下：

a) 取pq横线下部为研究对象，在横截面范围内分布着切应力，虽然根据假设这条线上的切应力相等，但是切应力在横截面上沿竖向并非均匀分布，所以不能直接通过求合力的方法求解。

b）根据切应力互等定理，隔离体顶面（即rp面）分布着切应力且与所求应力相等。

c）因为取出的隔离体长度为dx，很短，所以可以将整个顶面上的切应力近似看作均匀分布，于是合力易求。

d）最后，因为顶面切应力沿x轴方向，所以对隔离体列x方向的受力平衡方程，方程中的力包括了顶面切应力的合力和两个横截面上的正应力的合力，解方程即得。

4）结果分析

注意最终得出的计算公式，该公式计算出的是横截面某一水平线上的切应力，这一横线的位置要素体现在的计算中。

欢迎关注微信公众号：『结构工程师成长记』，更多学习心得期待与您分享。

「封图来源：Pixabay」