knn算法python代码_50行代码用Python实现遗传进化算法

学习如何用不到50行的代码从头开始编写简单的Evolutionary Algorithm，这些代码可用于您的项目。 包含2个示例！

Photo by Johannes Plenio on Unsplash

进化算法是解决诸如优化问题之类的计算问题的特殊方法。 它们通常会在合理的时间内产生非常好的结果，而无需我们对特定于问题的属性进行大量思考。 通常，我们只需要调整一些参数，然后运行一个相当通用的框架并为我们提供解决方案。 您将在本文中看到如何在Python中实现这种通用框架。

当处理极端困难的问题(例如NP完全问题)时，这尤其有趣。 这些是许多公司每天都必须解决的现实问题，而我们不知道任何有效的算法。 这些问题之一是旅行商问题(TSP)的优化版本，其表达方式如下：

推销员想在n个城市出售他的商品。他从城市1开始，以某种顺序一次访问其他n-1个城市，然后再次返回城市1。为了使出行距离最小化，游览城市的最佳顺序是什么？

我们稍后将再次讨论这个问题，作为应用我们的进化算法的一个重要例子。但是在我们去那里之前，让我们看看什么是进化算法以及如何将它们应用到一个简单的例子中。

一个有趣的例子：MarI / O

进化算法的一个有趣的应用是Seth Bling在" NEAT"论文的基础上构建的MarI / O [3]。 使用进化算法从头开始构建复杂的神经网络架构，以玩经典的《超级马里奥世界》。 怀旧开始。

进化算法

现在，我们将看到如何开发一种进化算法来解决一个简单的函数最大化问题，即，我们想要找到使给定函数f的输出最大化的输入x。 例如，对于f(x，y)=-(x²+y²)，唯一解是(x，y)=(0，0)。

该算法也可以轻松地用于解决TSP和其他问题。 但是首先，让我们看看进化算法实际上是什么。

动机

进化算法的设计类似于自然界的进化。其中，这三个概念是进化的核心：

1. 有一群人。
2. 个人可以繁殖和死亡。 这些事情的发生取决于它的适用性。 适应度越高，个体的属性(DNA)在个体本身或后代中停留的时间就越长。
3. 个人可以变异，即稍微改变其属性。

我们可以使用这些概念来创建一个元算法，即一种内部使用我们尚未指定的其他算法的算法来解决我们的问题。 不用担心，我们会立即为您充满生命。

元算法

1. 随机生成初始个体。
2. 评估人口中每个人的健康状况。
3. 尽可能重复一次：a)选择一个具有良好适应能力得分的个体进行繁殖。b)让他们产生后代。c)对这些后代进行突变。d)评估种群中每个个体的适应性。f)让个体具有繁殖力。 健
5. 评分不佳而死。
6. 选择适合度最高的个人作为解决方案。

等等，这很笼统，不是吗？ 有很多事情必须指定。

什么是个体？第一个种群中有多少个体？它们是如何产生的？哪些健身得分？多少父母产生了多少后代？ 究竟是什么？如何变异？有多少人死亡？重复多少次？

现在让我们使用函数最大化的问题来说明如何具体实现元算法。

一个简单的例子

让我们以区间[0，4]上的函数f(x)=-x(x-1)(x-2)(x-3)(x-4)为例。我们希望找到一些价值，以最大限度地发挥这一作用。一个潜在的问题可能是1.4附近的局部最大值，我们不想找到它！

The x maximizing f is about 3.6, with a maximal value of also about 3.6.

让我们看看是否可以使用进化算法来重现此内容。 因此，让我们开始回答所有未解决的问题。

有哪些个人？

个人永远是问题的潜在解决方案。

在我们的示例中，数字介于0和4之间，因为我们仅在此间隔内考虑此函数。 这个很容易，对吧？ 我保证，这不会比这困难得多。

第一批人口中有多少个人？他们是如何产生的？

个人数量是您必须组成的超参数。 如果您对解决方案一无所知，请尽可能随机选择初始种群。

在我们的例子中，我们如何使用10个随机的个体，这些随机的个体均匀地画出0到4之间的数字？

我希望使用统一随机元素是一个不错的选择，因为我们可以很好地覆盖整个解决方案空间。 例如，如果我们使用均值为1.4的正态分布，也许我们会将解决方案也推到1.4附近的错误局部最大值。

I have started with the individuals about 0.596, 1.067, 1.184, 1.431, 1.641, 1.792, 2.068, 2.495, 3.169, and 3.785.

哪个适应性得分？

我们也必须弥补这一点。 我们的解决方案应具有最高的适应性得分。

我们希望最大化函数f，因此我们可以只使用函数f本身。

The right-most individual has the highest fitness score of about 3.1. Some individuals have fitness scores of about 1 and three individuals even have a negative fitness score.

有多少父母生产多少后代？ 以及究竟如何？

我们也必须弥补这一点。 所有的。

在我们的示例中，我们总是可以使用两个人来产生一个后代。 我们也可以让它们生产更多，但让我们从这里轻松开始。 因此，如果我们有两个人(也称为父母)，那么他们的后代可能就是他们的综合。 例如，1.1和3.5的后代可以是2.3。 总共让我们产生三个后代，总共使用六个不同的父母(即每个父母只有一个伴侣)。

同样，这些都是我任意决定的事情。 您也可以使用其他策略来执行此步骤！ 每个后代使用一个或三个父母，使父母得到五个后代，一起玩。

适应度最高的六个人是数字1.792、1.184、3.169、1.641、1.431和3.785(按适应性升序排列)。 现在，假设此列表中的两个邻居有一个后代：

• 1.792与1.184：1.488
• 3.169和1.641：2.405
• 1.431和3.785：2.608

The miracle of life!

如何变异？

概率性地改变后代。 这是在不同地方探索更多可能解决方案的好方法，并且不会确定性地走错路。

在我们的例子中，我们可以给每个后代加上高斯噪声。 平均值为零，标准偏差为0.25很好。 另外，请记住：

个人必须成为潜在的解决方案！ 因此，突变一定不能将孩子赶出可行的区间[0，4]。 如果发生这种情况，请将子级设置为间隔的最近边缘。

The orange points shifted a bit after the mutation.

有多少人死亡？

随你喜欢。 在整个步骤中保持种群大小相同可能是件好事，因为否则种群数量可能会爆炸或每个人都在某个时间死亡。

由于我们现在的人口中有13个人，因此让其中3个人死亡，最终我们会剩下10个人。 让我们选择适应性最差的那些，即旧个人0.596和2.495，以及新创建的个人2.121。

The circle of life.

重复多久一次？

随你喜欢。 有时只需检查一下，直到发现解决方案不再变得更好为止。

也许让我们尝试50个纪元，然后看看会发生什么。 经过我们的人工进化，我们可以检查所有个体并选择得分最高的个体作为解决问题的方法。

直到时代的演变。 50个看起来像这样：

我们可以看到该算法有效！ 但这似乎是一个紧要关头。 直到第25个时代，人口都在x = 1.4附近聚集其他局部最大值。 幸运的是，我们有一个远在4岁的人，从第25个时代开始就成功地将人口拉到了右侧。

当查看每个时期人口中最佳个体的适应度得分时，我们还可以看到在时期25周围的这种转变。

It skyrocketed at around epoch 25.

讨论区

好的，我们已经了解了算法的工作原理，并最终获得了正确答案(或至少非常好的近似值)！ 有点运气，但这永远都是一样的。 我们可能会更不幸，我们的初始人口可能始于x = 1.4的局部最大值附近。 那么，个人突破该区域的可能性就很小，如本例所示：

A failed attempt. The algorithm only finds the wrong local maximum.

仍然可能是突变将一个人推向右侧，这反过来又吸引了更多的人。 但这极不可能发生，因为标准偏差为0.25，因此突变在任何方向上最多将个体推向0.75的可能性> 99％。

那么，使用更极端的变异好吗？ 好吧，如果我们夸大其词，个人只会跳到整个地方或聚集在x = 0和x = 4的角落。 因此，我们在这里选择参数时必须谨慎。

从理论上讲，您可以将演化算法视为高度随机化的算法。初始种群是随机的，个体通过或多或少的复杂操作产生后代，后代利用随机性进行变异，所有这些重复了数百，数千，数百万次。

因此，很难分析这些算法并对其成功概率或结果质量给出任何理论上的界限。 对于非常简单的算法，这是可能的，例如用于最大化极简单函数的(1 + 1)进化算法[1]或用于解决简化多目标背包问题[2]的算法，但是很少看到这样的示例。

但是，如果运行不起作用，请使用相同或其他参数再次尝试。

用Python实现

在这里，我将与您分享我的实现。 我试图使它具有一般性和抽象性，因此您可以轻松地将其用于您的目的。

如果您以前从未使用过Abstract Base Classes，请不用担心。 "Individual"类仅用于告诉您必须对代表个人的对象使用哪个接口。 您的个人需要一个值(有效载荷，潜在解决方案)，您必须实现随机初始化，变异和配对功能。

import numpy as npfrom abc import ABC, abstractmethodclass Individual(ABC):    def __init__(self, value=None, init_params=None):        if value is not None:            self.value = value        else:            self.value = self._random_init(init_params)    @abstractmethod    def pair(self, other, pair_params):        pass    @abstractmethod    def mutate(self, mutate_params):        pass    @abstractmethod    def _random_init(self, init_params):        passclass Optimization(Individual):    def pair(self, other, pair_params):        return Optimization(pair_params['alpha'] * self.value + (1 - pair_params['alpha']) * other.value)    def mutate(self, mutate_params):        self.value += np.random.normal(0, mutate_params['rate'], mutate_params['dim'])        for i in range(len(self.value)):            if self.value[i] < mutate_params['lower_bound']:                self.value[i] = mutate_params['lower_bound']            elif self.value[i] > mutate_params['upper_bound']:                self.value[i] = mutate_params['upper_bound']    def _random_init(self, init_params):        return np.random.uniform(init_params['lower_bound'], init_params['upper_bound'], init_params['dim'])class Population:    def __init__(self, size, fitness, individual_class, init_params):        self.fitness = fitness        self.individuals = [individual_class(init_params=init_params) for _ in range(size)]        self.individuals.sort(key=lambda x: self.fitness(x))    def replace(self, new_individuals):        size = len(self.individuals)        self.individuals.extend(new_individuals)        self.individuals.sort(key=lambda x: self.fitness(x))        self.individuals = self.individuals[-size:]    def get_parents(self, n_offsprings):        mothers = self.individuals[-2 * n_offsprings::2]        fathers = self.individuals[-2 * n_offsprings + 1::2]        return mothers, fathersclass Evolution:    def __init__(self, pool_size, fitness, individual_class, n_offsprings, pair_params, mutate_params, init_params):        self.pair_params = pair_params        self.mutate_params = mutate_params        self.pool = Population(pool_size, fitness, individual_class, init_params)        self.n_offsprings = n_offsprings    def step(self):        mothers, fathers = self.pool.get_parents(self.n_offsprings)        offsprings = []        for mother, father in zip(mothers, fathers):            offspring = mother.pair(father, self.pair_params)            offspring.mutate(self.mutate_params)            offsprings.append(offspring)        self.pool.replace(offsprings)

然后由Pool和Evolution类负责其余的工作。 我还实现了函数最大化示例，以向您展示其外观。 我在那里使用了一些其他参数，但是如果将所有下限都替换为0，将所有下限替换为4，将比率替换为0.25，将dim替换为1，并且alpha = 0.5，您将再次得到我们的示例。

您可以像下面这样使用这些类：

from evo import Evolution, Optimizationdef fitness(opt):    return -opt.value[0] * (opt.value[0] - 1) * (opt.value[0] - 2) * (opt.value[0] - 3) * (opt.value[0] - 4)evo = Evolution(    pool_size=10, fitness=fitness, individual_class=Optimization, n_offsprings=3,    pair_params={'alpha': 0.5},    mutate_params={'lower_bound': 0, 'upper_bound': 4, 'rate': 0.25, 'dim': 1},    init_params={'lower_bound': 0, 'upper_bound': 4, 'dim': 1})n_epochs = 50for i in range(n_epochs):    evo.step()print(evo.pool.individuals[-1].value)

然后离开！

到目前为止，我们已经对小玩具问题有了一定的信心，但是现在是时候重新回到困难的TSP了。

旅行推销员问题

TSP旨在找到n个城市之间最短的往返路程。 使用这些作为示例：

Ten cities on a map.

TSP的解决方案如下所示：

The shortest round trip visiting all cities.

一些事实

存在许多算法来解决这一问题。 它们的范围从详尽的搜索(尝试所有方法)到更复杂的算法。 但是，所有这些方法都很慢，并且如果P≠NP，我们将永远无法期待任何快速算法。

如果可以等待几天，详尽的搜索将使您最多可以解决15个城市的问题。 其他方法(例如Held-Karp算法)使您可以乐观地求解多达30–50个城市的实例。

如果您不再需要最佳解决方案，那么1976年的Christofides算法将在很短的时间内为您提供解决方案，与最短的往返时间相比，最长可证明延长了50％。

想想为什么这是一个很棒的结果：我们甚至都不知道最短的往返长度，但是仍然可以说，这种算法的往返收益比这个未知的解决方案长不到50％！

但是，现在，让我们为您提供等待的结果：一种解决TSP的进化算法！

一种求解TSP的进化算法

这次，我们从20个城市开始。 数量仍然很低，无法使用Held-Karp算法解决，因此我们甚至可以检查最终是否获得了最佳解决方案！ 这是地图：

Twenty cities on a map. Let's not even bother trying an exhaustive search on this one. Maybe these cities don't even exist anymore until we get the shortest round trip.

现在，我们必须再次回答所有问题。 让我们首先回答更简单的"数字问题"(如果事情不起作用，我们可以轻松调整的超参数)：

• 多少代？ 1000
• 有多少个起始个人？ 100
• 有多少父母？ 60(两个像以前一样生出一个后代)
• 有多少后代？ 30
• 有多少垂死的人？ 30

令人兴奋的问题是关于我们现在必须定义的类TSP的实现。 有哪些个人？ 随机初始化如何工作？ 配对？ 突变？ 健身得分是多少？

初始人口

让我们从一个基本的开始：这里的个人是什么？ 提示：这不是城市。 再次：

个人永远是问题的潜在解决方案。

对于TSP，我们搜索短程往返。 "短"是指往返中每两个城市之间的欧几里得距离之和。 我们可以将这样的往返表示为n个数字的列表，例如 (0、3、1)显示为"从城市0开始，然后转到城市3，从那里到城市1，然后回到城市0。"。 因此，我们的个人是一个数字列表，每个数字从0到n-1恰好包含一次，即{0，1，2，…，n-1}上的排列。

在整个过程中，我们必须维护此属性。 保留人口中的某个个体并不能代表该问题的可行解决方案是没有意义的，因为它阻塞了人口，我们甚至可能最终选择它，从而给我们提供了无效的解决方案。

以及如何初始化它们？ 好吧，只是对数字从0到n-1进行随机排列。 这应该做的工作。

def _random_init(self, init_params):    return np.random.choice(        a=range(init_params['n_cities']),        size=init_params['n_cities'],        replace=False    )

让我们继续进行突变过程。

突变

那么，我们如何以一种简单的方式改变往返行程呢？ 想象一下，我们有一个往返于五个城市的旅行，例如(3、1、4、2、0)。 一种简单的方法是随机交换两个元素。 我们的示例可以更改为(0，1，4，2，2，3)或(3，4，1，2，0)。 我们还可以交换多次，并使其中的超参数速率与之前的函数最大化示例中的标准偏差相当。

def mutate(self, mutate_params):    for _ in range(mutate_params['rate']):        i, j = np.random.choice(            a=range(len(self.value)),            size=2,            replace=False)        self.value[i], self.value[j] = self.value[j], self.value[i]

显然，这种突变保留了属性，即个体是置换，即可行的解决方案。

这里最有趣的事情可能是pair函数。

配对

让我们假设我们有以下要用作父母的个人：

您可以执行以下操作：将第二个人的右半部分复制到第一个人的右半部分。

The right half of the first individual gets replaced. The 4 replaces the old 5, 2 replaces 3, and 3 replaces 1.

我们现在要使用更改后的第一个个体作为后代，但是由于现在有重复的数字，因此无法按原样工作。 因此，必须首先修复变更后的第一个人的左半部分。 我们可以这样做：

插入右半部分的4踢出了之前的5。 因此，让我们将左半部分的4替换为5，因为现在缺少了。 用2踢出3来做同样的事情，得出以下结果：

但是还有一个问题：我们现在两次有3。 但是我们可以重复此过程多次，直到再次获得可行的个体为止。 3是问题所在。 它最初以1踢出。因此用左1替换左3，然后瞧：后代是(0，5，1，4，4，2，3)。

实现

总的来说，我们的TSP类如下所示：

class TSP(Individual):    def pair(self, other, pair_params):        self_head = self.value[:int(len(self.value) * pair_params['alpha'])].copy()        self_tail = self.value[int(len(self.value) * pair_params['alpha']):].copy()        other_tail = other.value[int(len(other.value) * pair_params['alpha']):].copy()        mapping = {other_tail[i]: self_tail[i] for i in range(len(self_tail))}        for i in range(len(self_head)):            while self_head[i] in other_tail:                self_head[i] = mapping[self_head[i]]        return TSP(np.hstack([self_head, other_tail]))    def mutate(self, mutate_params):        for _ in range(mutate_params['rate']):            i, j = np.random.choice(range(len(self.value)), 2, replace=False)            self.value[i], self.value[j] = self.value[j], self.value[i]    def _random_init(self, init_params):        return np.random.choice(range(init_params['n_cities']), init_params['n_cities'], replace=False)

在这里，我还介绍了另一个超参数alpha，它决定了在何处分割个人。 在我的示例中，我使用alpha = 0.5。

适应性得分

由于我们希望最小化往返行程的长度，因此我们可以使用减去往返行程的长度作为适应度得分。

实验

让我们用20个城市解决TSP！ 我使用以下代码：我定义了适应度函数，一个用于计算往返长度的函数以及一个用于计算距离矩阵(两个城市之间的成对距离)的函数。

import numpy as npfrom evo import Evolution, TSPimport matplotlib.pyplot as pltdef tsp_fitness_creator(cities):    matrix = []    for city in cities:        row = []        for city_ in cities:            row.append(np.linalg.norm(city - city_))        matrix.append(row)    distances = np.array(matrix)    def fitness(tsp):        res = 0        for i in range(len(tsp.value)):            res += distances[tsp.value[i], tsp.value[(i + 1) % len(tsp.value)]]        return -res    return fitnessdef compute_distances(cities):    distances = []    for from_city in cities:        row = []        for to_city in cities:            row.append(np.linalg.norm(from_city - to_city))        distances.append(row)    return np.array(distances)def route_length(distances, route):    length = 0    for i in range(len(route)):        length += distances[route[i], route[(i + 1) % len(route)]]    return lengthdef plot_route(cities, route, distances):    length = route_length(distances, route)    plt.figure(figsize=(12, 8))    plt.scatter(x=cities[:, 0], y=cities[:, 1], s=1000, zorder=1)    for i in range(len(cities)):        plt.text(cities[i][0], cities[i][1], str(i), horizontalalignment='center', verticalalignment='center', size=16,                 c='white')    for i in range(len(route)):        plt.plot([cities[route[i]][0], cities[route[(i + 1) % len(route)]][0]],                 [cities[route[i]][1], cities[route[(i + 1) % len(route)]][1]], 'k', zorder=0)    if len(route)>0:        plt.title(f'Visiting {len(route)} cities in length {length:.2f}', size=16)    else:        plt.title(f'{len(cities)} cities', size=16)    plt.show()cities = np.array([[35, 51],                   [113, 213],                   [82, 280],                   [322, 340],                   [256, 352],                   [160, 24],                   [322, 145],                   [12, 349],                   [282, 20],                   [241, 8],                   [398, 153],                   [182, 305],                   [153, 257],                   [275, 190],                   [242, 75],                   [19, 229],                   [303, 352],                   [39, 309],                   [383, 79],                   [226, 343]])fitness = tsp_fitness_creator(cities)distances = compute_distances(cities)evo = Evolution(    pool_size=100, fitness=fitness, individual_class=TSP, n_offsprings=30,    pair_params={'alpha': 0.5},    mutate_params={'rate': 1},    init_params={'n_cities': 20})n_epochs = 1000hist = []for i in range(n_epochs):    hist.append(evo.pool.fitness(evo.pool.individuals[-1]))    evo.step()plt.plot(hist)plt.show()plot_route(cities, route=evo.pool.individuals[-1].value, distances=distances)

对我来说，适应度函数的行为如下：

以下是每个时代的最佳个人：

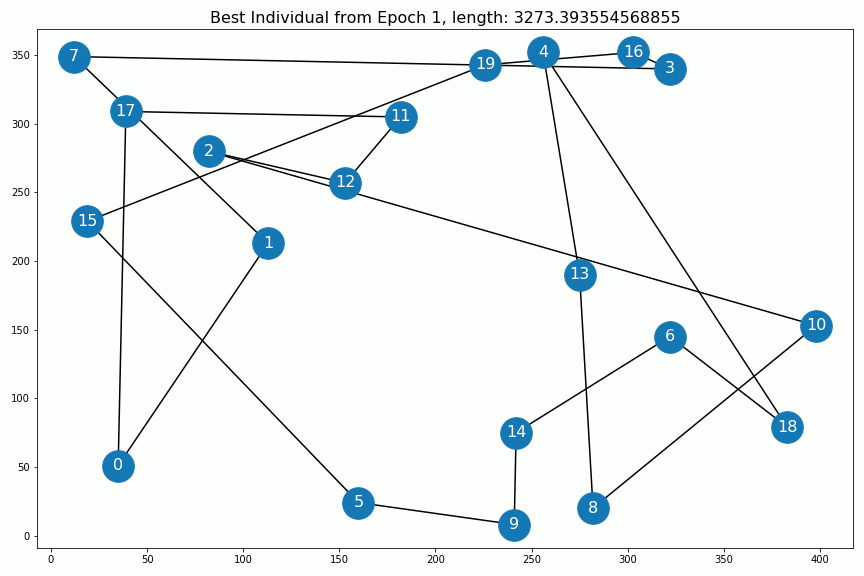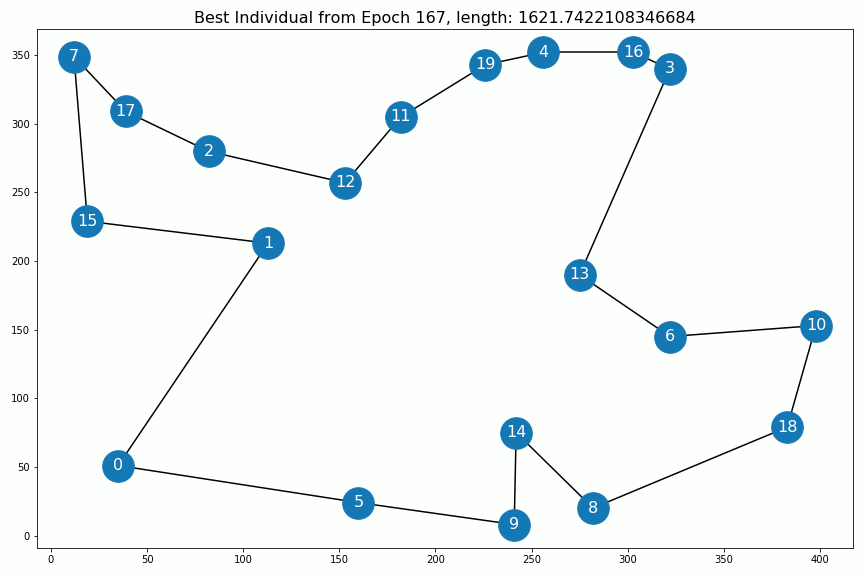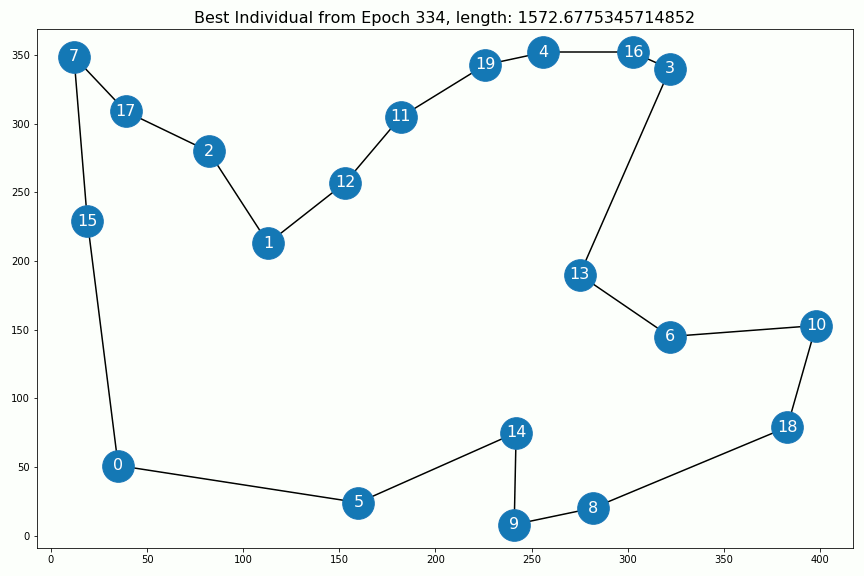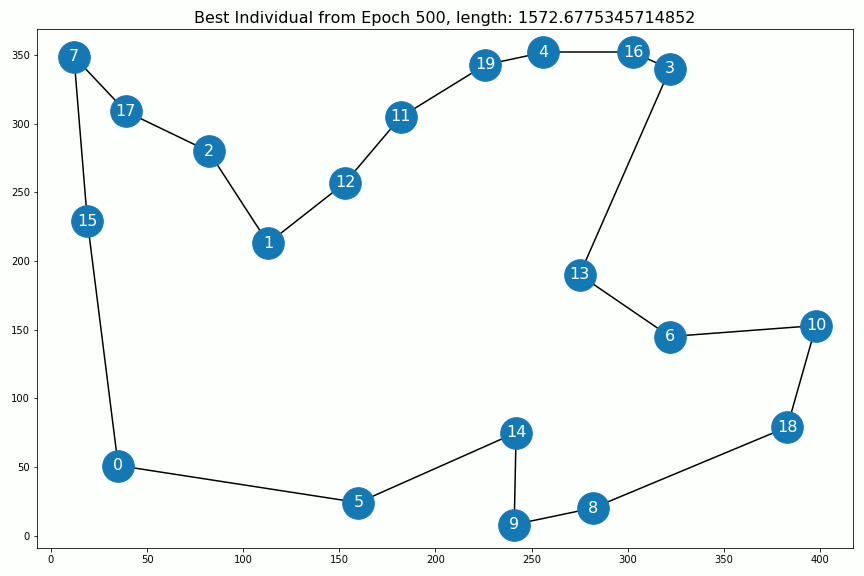
The evolution of the solution. After epoch 400 nothing changes anymore.

更多城市！

对于最后一幕，让我们尝试一些非常困难的事情。 不仅有10个或20个城市，而且还有100个城市，这对于任何精确的算法来说都太多了。

From a very chaotic to a much cleaner and shorter round trip.

我不能告诉你这是否是最快的往返行程，但是对我来说，这绝对是一个不错的选择！

结论

在本文中，我们通过两个示例了解了进化算法的工作原理：最大化函数并解决Traveling Salesman问题。进化算法通常用于解决我们不知道确切答案的难题。该算法可以非常快速并产生准确的结果。实施起来很容易，并且您不必成为问题所在领域的专家，例如您无需阅读过去20年来TSP研究的论文即可编写出性能出色的算法。

可悲的是，很难获得任何理论结果，因为进化算法通常会以复杂的方式交互作用于许多随机性。 因此，我们不知道给出的解决方案是好是坏，我们只能检查它对于我们的用例是否足够好。 在100个城市的示例中，如果我们的目标是前往每个城市的长度不超过15万，则该算法为我们提供了一个完美的答案。

参考文献

[1] S. Droste，T。Jansen和I. Wegener，关于(1 + 1)进化算法的分析(2002)，理论计算机科学，第276卷，第1-2期，2002年4月6日，第51页–81

[2] M. Laumanns，L。Thiele和E. Zitzler，关于简化多目标背包问题的进化算法的运行时间分析(2004)，自然计算3，37–51

[3] K. Stanley，R。Miikkulainen，"通过增强拓扑结构演化神经网络(2002)，进化计算10(2)2002，S。99-127"

我希望我能教给你一些有用的东西。

谢谢阅读！

(本文翻译自Dr. Robert Kübler的文章《An extensible Evolutionary Algorithm Example in Python》，参考：https://towardsdatascience.com/an-extensible-evolutionary-algorithm-example-in-python-7372c56a557b)