matlab设计凸轮轮廓代码_凸轮设计很难，为何高端设备要用凸轮，如何学凸轮设计附学习资料...

点击上方“机械设计一点通”关注我们，每天学习一个机械设计相关知识点

---

凸轮结构的应用及优点

凸轮机构是由凸轮，从动件和机架三个基本构件组成的高副机构，凸轮是一个具有曲线轮廓或凹槽的构件，一般为主动件，作等速回转运动或往复直线运动。

只需设计适当的凸轮轮廓，便可使从动件得到任意的预期运动，而且结构简单、紧凑、设计方便，因此在自动机床、轻工机械、纺织机械、印刷机械、食品机械、包装机械和机电一体化产品中得到广泛应用。凸轮机构最大的优点是可实现高速化，结构紧凑，可靠性高；最大的缺点是不可变，不能变更动作时间(角度) 。

之前有个客户研发了一台纯凸轮结构的设备，设计了用了不少异形凸轮，产量比以前的老机型高了很多；而且很多前辈也这么说，他们接触到的很多国外设备也都是这样的。

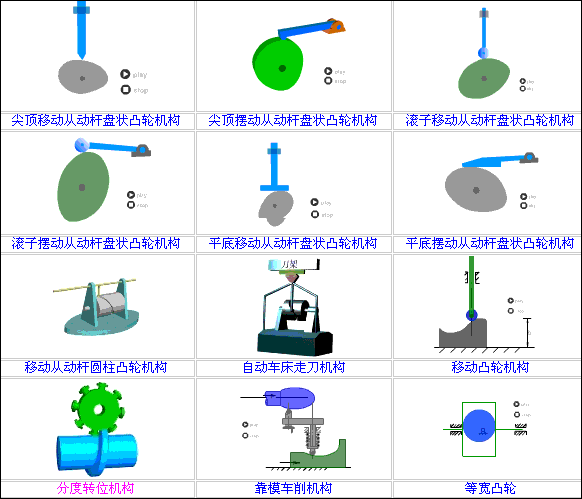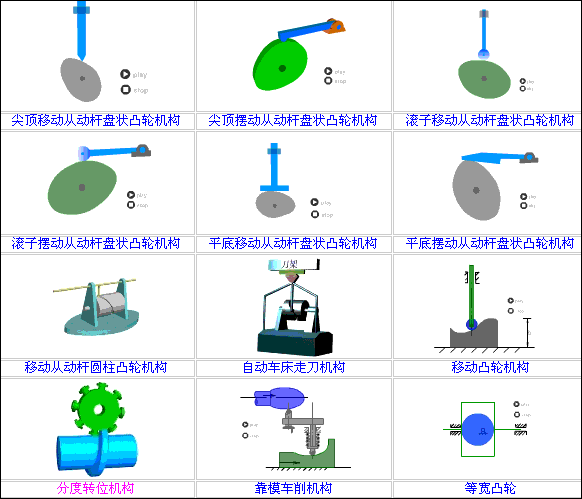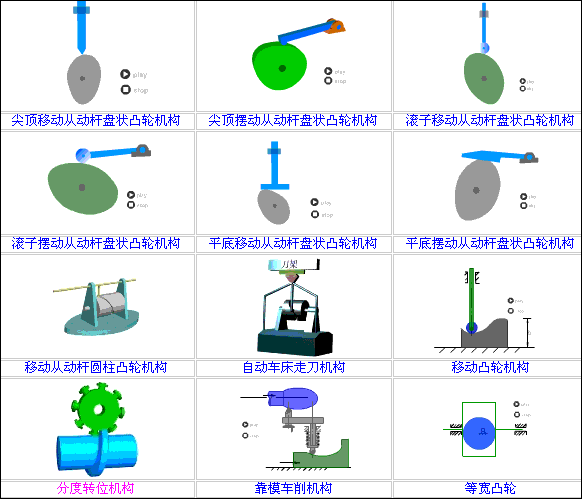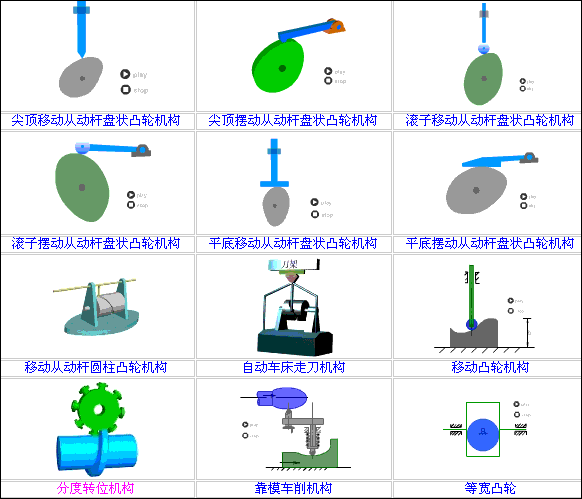
如何学凸轮结构的设计

(玩凸轮，数学没过关，就尽早放弃)玩凸轮系统，先念数学，数学不过关就放弃，甭玩，这么最省心，否则，矢量问题，微积分就不懂，怎么玩都白搭，一个矢量关系是明摆着的问题，修正一下就解决了所有问题，而不会这个，那个机器就一直玩不出来，就像买一辆没有发动机的汽车，完全没有意义，多看，多学，多积累，从纯数学关系式开始学，矢量问题，受力问题，一直学到扭转振动，把扭振学好了，可以处理凸轮轴的扭转振动了，就70%过关，以后就看造化了。

浅谈凸轮的设计

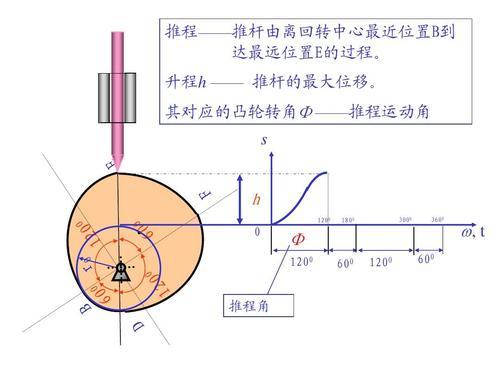
凸轮设计应该分成三步，第一步是参数确定，就是根据从动件的动作要求，确定凸轮的各种初始参数，以摆动从动件凸轮为例，像凸轮旋转速度，摆杆长度，最小和最大理论轮廓半径，摆杆中心位置，凸轮旋转方向，如果有共轭的话还有主副摆杆夹角等参数，。

第二步是凸轮曲线设计，举个例子，一辆车从A地到B地，路程(这个路程的长短是在第一步里确定的)是一定的，速度和时间是驾驶员掌控的，到底要省油呢，还是要安全呢，还是要快呢，还是要车子损耗少呢。这就要驾驶员自己去掌控。这么多要求之间是要互相权衡的，没有最好，只有根据要求，哪个更合理，更接近理想。凸轮设计时，我们就是驾驶员，要设计出一条最合理的凸轮曲线，以满足工况的要求。凸轮与凸轮曲线之间的关系：凸轮其实就是带有不规则轮廓的零部件，而凸轮曲线是从动件的运动曲线，凸轮曲线的设计宗旨是在满足机械运动的前提下，使得从动件走的尽量圆滑，无振动，耗能少。对于我们平时设计凸轮，一般的凸轮曲线，只对从动件最终位置有要求的话，正弦曲线就算很好的选择，也可选修正正弦，梯形等。当然时候还有对从动件在某个时间点的速度甚至加速度更甚至跃度有要求。

虽然这种情况少，但真碰到，要设计的话，可是得花很长时间去计算的，需要数学功底的。其实凸轮曲线更广泛的应用应该是在伺服电机上，只不过我们学机械的称为凸轮曲线，而搞伺服电机的称为曲线而已，在权衡最大速度，最大加速度，时间，振动，负载，电机电流，脉冲频率等过程中，设计出一条最好的运动曲线。

第三步，凸轮设计根据第二步计算得出的最大速度，最大加速度，惯性矩等值，计算出凸轮面所受的最大载荷，再根据凸轮本身旋转速度，润滑条件，工作温度，与凸轮接触的零件的材料(通常为滚子)，选择合理的材料，厚度，热处理方式等。当然凸轮设计还要考虑机加工零位，装配零位，微调方便，从动件拆起来方便等。如果是弹性封闭凸轮的话，还要考虑弹簧的寿命等。

附凸轮设计相关学习资料，有兴趣有需要的粉丝朋友可以直接复制文章标题发私信给小编，即可自动获取免费下载链接

---

欢迎大家在评论处补充你认为文章中有解释不对或欠缺的部分，这样下一个阅读的人就会学到更多，你知道的正是大家需要的。。。